二部圖------KM演算法、匈牙利演算法
二分圖的概念
二分圖又稱作二部圖，是圖論中的一種特殊模型。 設G=(V, E)是一個無向圖。如果頂點集V可分割為兩個互不相交的子集X和Y，並且圖中每條邊連線的兩個頂點一個在X中，另一個在Y中，則稱圖G為二分圖。
二分圖的性質
定理：當且僅當無向圖G的每一個迴路的次數均是偶數時，G才是一個二分圖。如果無迴路，相當於任一回路的次數為0，故也視為二分圖。
二分圖匹配
給定一個二分圖G，在G的一個子圖M中，M的邊集{E}中的任意兩條邊都不依附於同一個頂點，則稱M是一個匹配。 圖中加粗的邊是數量為2的匹配。
最大匹配
選擇邊數最大的子圖稱為圖的最大匹配問題(maximal matching problem) 如果一個匹配中，圖中的每個頂點都和圖中某條邊相關聯，則稱此匹配為完全匹配，也稱作完備匹配。 圖中所示為一個最大匹配，但不是完全匹配。
增廣路徑
增廣路徑的定義：設M為二分圖G已匹配邊的集合，若P是圖G中一條連通兩個未匹配頂點的路徑（P的起點在X部，終點在Y部，反之亦可），並且屬M的邊和不屬M的邊(即已匹配和待匹配的邊)在P上交替出現，則稱P為相對於M的一條增廣路徑。 增廣路徑是一條“交錯軌”。也就是說, 它的第一條邊是目前還沒有參與匹配的,第二條邊參與了匹配,第三條邊沒有..最後一條邊沒有參與匹配,並且起點和終點還沒有被選擇過，這樣交錯進行,顯然P有奇數條邊（為什麼？）
尋找增廣路徑
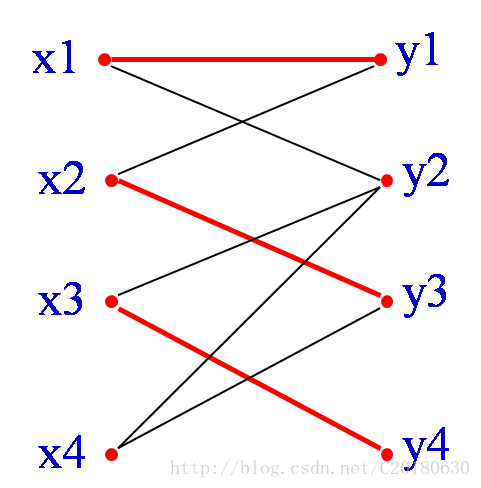
如果從M中抽走{x2,y3},{x1,y1}，並加入{x4,y3},{x2, y1}, {x1,y2}，也就是將增廣路所有的邊進行”反色”,則可以得到四條邊的匹配M’={{x3,y4}, {x4,y3},{x2, y1}, {x1,y2}} 容易發現這樣修改以後,匹配仍然是合法的,但是匹配數增加了一對。另外,單獨的一條連線兩個未匹配點的邊顯然也是交錯軌.可以證明,當不能再找到增廣軌時,就得到了一個最大匹配.這也就是匈牙利演算法的思路. 可知四條邊的匹配是最大匹配
增廣路徑性質 由增廣路的定義可以推出下述三個結論：
P的路徑長度必定為奇數，第一條邊和最後一條邊都不屬於M，因為兩個端點分屬兩個集合，且未匹配。 P經過取反操作可以得到一個更大的匹配M’。 M為G的最大匹配當且僅當不存在相對於M的增廣路徑。 匈牙利演算法 用增廣路求最大匹配(稱作匈牙利演算法，匈牙利數學家Edmonds於1965年提出) 演算法輪廓：
置M為空 找出一條增廣路徑P，通過取反操作獲得更大的匹配M’代替M 重複2操作直到找不出增廣路徑為止 找增廣路徑的演算法 我們採用DFS的辦法找一條增廣路徑： 從X部一個未匹配的頂點u開始，找一個未訪問的鄰接點v（v一定是Y部頂點）。對於v，分兩種情況：
如果v未匹配，則已經找到一條增廣路 如果v已經匹配，則取出v的匹配頂點w(w一定是X部頂點)，邊(w,v)目前是匹配的，根據“取反”的想法，要將(w,v)改為未匹配，(u,v)設為匹配，能實現這一點的條件是看從w為起點能否新找到一條增廣路徑P’。如果行，則u-v-P’就是一條以u為起點的增廣路徑。 匈牙利演算法 cx[i]表示與X部i點匹配的Y部頂點編號 cy[i]表示與Y部i點匹配的X部頂點編號
//虛擬碼
bool dfs(int u)//尋找從u出發的增廣路徑
{
for each v∈u的鄰接點
if(v未訪問){
標記v已訪問;
if(v未匹配||dfs(cy[v])){
cx[u]=v;
cy[v]=u;
return true;//有從u出發的增廣路徑
}
}
return false;//無法找到從u出發的增廣路徑
}
//程式碼
bool dfs(int u){
for(int v=1;v<=m;v++)
if(t[u][v]&&!vis[v]){
vis[v]=1;
if(cy[v]==-1||dfs(cy[v])){
cx[u]=v;cy[v]=u;
return 1;
}
}
return 0;
}
void maxmatch()//匈牙利演算法主函式
{
int ans=0;
memset(cx,0xff,sizeof cx);
memset(cy,0xff,sizeof cy);
for(int i=0;i<=nx;i++)
if(cx[i]==-1)//如果i未匹配
{
memset(visit,false,sizeof(visit)) ;
ans += dfs(i);
}
return ans ;
} 一般對KM演算法的描述，基本上可以概括成以下幾個步驟： （1） 初始化可行標杆 （2） 用匈牙利演算法尋找完備匹配 （3） 若未找到完備匹配則修改可行標杆 （4） 重複（2）（3）直到找到相等子圖的完備匹配 KM演算法是用於尋找帶權二分圖最佳匹配的演算法。 二分圖：所有頂點可以分成兩個集：X和Y，其中X和Y中的任意兩個在同一個集中的點都不相連，而來自X集的頂點與來自Y集的頂點有連線。當這些連線被賦於一定的權重時，這樣的二分圖便是帶權二分圖。 二分圖匹配是指求出一組邊，其中的頂點分別在兩個集合中，且任意兩條邊都沒有相同的頂點，這組邊叫做二分圖的匹配，而所能得到的最大的邊的個數，叫做二分圖的最大匹配。
匈牙利演算法
一般用於尋找二分圖的最大匹配。演算法根據一定的規則選擇二分圖的邊加入匹配子圖中，其基本模式為：
初始化匹配子圖為空
While 找得到增廣路徑
Do 把增廣路徑新增到匹配子圖中
增廣路徑有如下特性：
1. 有奇數條邊
2. 起點在二分圖的X邊，終點在二分圖的Y邊
3. 路徑上的點一定是一個在X邊，一個在Y邊，交錯出現。
4. 整條路徑上沒有重複的點
5. 起點和終點都是目前還沒有配對的點，其他的點都已經出現在匹配子圖中
6. 路徑上的所有第奇數條邊都是目前還沒有進入目前的匹配子圖的邊，而所有第偶數條邊都已經進入目前的匹配子圖。奇數邊比偶數邊多一條邊
7. 於是當我們把所有第奇數條邊都加到匹配子圖並把條偶數條邊都刪除，匹配數增加了1.
例如下圖，藍色的是當前的匹配子圖，目前只有邊x0y0，然後通過x1找到了增廣路徑：x1y0->y0x0->x0y2 
其中第奇數第邊x1y0和x0y2不在當前的匹配子圖中，而第偶數條邊x0y0在匹配子圖中，通過新增x1y0和x0y2到匹配子圖並刪除x0y0，使得匹配數由1增加到了2。每找到一條增廣路徑，通過新增刪除邊，我們總是能使匹配數加1.
增廣路徑有兩種尋徑方法，一個是深搜，一個是寬搜。
例如從x2出發尋找增廣路徑
深搜，x2找到y0匹配，但發現y0已經被x1匹配了，於是就深入到x1，去為x1找新的匹配節點，結果發現x1沒有其他的匹配節點，於是匹配失敗，x2接著找y1，發現y1可以匹配，於是就找到了新的增廣路徑。
寬搜，x2找到y0節點的時候，由於不能馬上得到一個合法的匹配，於是將它做為候選項放入佇列中，並接著找y1，於是匹配成功返回。相對來說，深搜要容易理解些，其棧可以由遞迴過程來維護，而寬搜則需要自己維護一個佇列，並對一路過來的路線自己做標記，實現起來比較麻煩。
對於帶權重的二分圖來說，我們可以把它看成一個所有X集合的頂點到所有Y集合的頂點均有邊的二分圖（把原來沒有的邊新增入二分圖，權重為0即可），也就是說它必定存在完備匹配（即其匹配數為min(|X|,|Y|)）。為了使權重達到最大，我們實際上是通過貪心演算法來選邊，形成一個新的二分圖（我們下面叫它二分子圖好了），並在該二分圖的基礎上尋找最大匹配，當該最大匹配為完備匹配時，我們可以確定該匹配為最佳匹配。（在這裡我們如此定義最大匹配：匹配邊數最多的匹配和最佳匹配：匹配邊的權重和最大的匹配。） 貪心演算法總是將最優的邊優先加入二分子圖，該最優的邊將對當前的匹配子圖帶來最大的貢獻，貢獻的衡量是通過標杆來實現的。下面我們將通過一個例項來解釋這個過程。
有帶權二分圖： 
演算法把權重轉換成標杆，X集跟Y集的每個頂點各有一個標杆值，初始情況下權重全部放在X集上。由於每個頂點都將至少會有一個匹配點，貪心演算法必然優先選擇該頂點上權重最大的邊（最理想的情況下，這些邊正好沒有交點，於是我們自然得到了最佳匹配）。最初的二分子圖為：（可以看到初始化時X標杆為該頂點上的最大權重，而Y標杆為0） 
從X0找增廣路徑，找到X0Y4；從而從X1找不到增廣路徑--->必須往二分子圖裡邊新增新的邊，使得X1能找到它的匹配，同時使權重總和新增最大。由於X1通往Y4而Y4已經被X0匹配，所以有兩種可能，①為X0找一個新的匹配點並把Y4讓給X1，②為X1找一個新的匹配點，現在我們將要看到標杆的作用了。
根據傳統的演算法描述，能夠進入二分子圖的邊的條件為L(x)+L(y)>=weight(xy)。當找不到增廣路徑時，對於搜尋過的路徑上的XY點，設該路徑上的X頂點集為S，Y頂點集為T，對所有在S中的點xi及不在T中的點yj，計算d=min{(L(xi)+L(yj)-weight(xiyj))}，從S集中的X標杆中減去d，並將其加入到T集中的Y的標杆中，由於S集中的X標杆減少了，而不在T中的Y標杆不變，相當於這兩個集合中的L(x)+L(y)變小了，也就是，有新的邊可以加入二分子圖了。從貪心選邊的角度看，我們可以為X0選擇新的邊而拋棄原先的二分子圖中的匹配邊，也可以為X1選擇新的邊而拋棄原先的二分子圖中的匹配邊，因為我們不能同時選擇X0Y4和X1Y4，因為這是一個不合法匹配，這個時候，d=min{(L(xi)+L(yj)-weight(xiyj))}的意義就在於，我們選擇一條新的邊，這條邊將被加入匹配子圖中使得匹配合法，選擇這條邊形成的匹配子圖，將比原先的匹配子圖加上這條非法邊組成的非法匹配子圖的權重和（如果它是合法的，它將是最大的）小最少，即權重最大了。好繞口的。用數學的方式表達，設原先的不合法匹配（它的權重最大，因為我們總是從權重最大的邊找起的）的權重為W，新的合法匹配為W’，d為min{W-W’i}。在這個例子中，S={X0, X1}，Y={Y4}，求出最小值d=L(X1)+L(Y0)-weight(X1Y0)=2，得到新的二分子圖： 
重新為X1尋找增廣路徑，找到X1Y0，可以看到新的匹配子圖的權重為9+6=15，比原先的不合法的匹配的權重9+8=17正好少d=2。
接下來從X2出發找不到增廣路徑，其走過的路徑如藍色的路線所示。形成的非法匹配子圖：X0Y4，X1Y0及X2Y0的權重和為22。在這條路徑上，只要為S={X0，X1，X2}中的任意一個頂點找到新的匹配，就可以解決這個問題，於是又開始求d。
d=L(X0)+L(Y2)-weight(X0Y2)=L(X2)+L(Y1)-weight(X2Y1)=1.
新的二分子圖為： 
重新為X2尋找增廣路徑，如果我們使用的是深搜，會得到路徑：X2Y0->Y0X1->X1Y4->Y4X0->X0Y2，即奇數條邊而刪除偶數條邊，新的匹配子圖中由這幾個頂點得到的新的權重為21；如果使用的是寬搜，會得到路徑X2Y1，另上原先的兩條匹配邊，權重為21。假設我們使用的是寬搜，得到的新的匹配子圖為： 
接下來依次類推，直到為X4找到一個匹配點。
KM演算法的最大特點在於利用標杆和權重來生成一個二分子圖，在該二分子圖上面找最大匹配，而且，當些僅當找到完備匹配，才能得到最佳匹配。標杆和權重的作用在於限制新邊的加入，使得加入的新邊總是能為子圖新增匹配數，同時又令權重和得到最大的提高。
下面是匈牙利演算法的dfs和bfs實現，是用c++實現的：
Cpp程式碼
//---------------------DFS---------------------------------
#include<iostream>
#include<memory.h>
using namespace std;
#define MAXN 10
int graph[MAXN][MAXN];
int match[MAXN];
int visitX[MAXN], visitY[MAXN];
int nx, ny;
bool findPath( int u )
{
visitX[u] = 1;
for( int v=0; v<ny; v++ )
{
if( !visitY[v] && graph[u][v] )
{
visitY[v] = 1;
if( match[v] == -1 || findPath(match[v]) )
{
match[v] = u;
return true;
}
}
}
return false;
}
int dfsHungarian()
{
int res = 0;
memset( match, -1, sizeof(match) );
for( int i=0; i<nx; i++ )
{
memset( visitX, 0, sizeof(visitX) );
memset( visitY, 0, sizeof(visitY) );
if( findPath(i) )
res++;
}
return res;
}
//-----------------------------BFS-------------------------------
#include<iostream>
#include<memory.h>
using namespace std;
#define MAXN 10
int graph[MAXN][MAXN];
//在bfs中，增廣路徑的搜尋是一層一層展開的，所以必須通過prevX來記錄上一層的頂點
//chkY用於標記某個Y頂點是否被目前的X頂點訪問嘗試過。
int matchX[MAXN], matchY[MAXN], prevX[MAXN], chkY[MAXN];
int queue[MAXN];
int nx, ny;
int bfsHungarian()
{
int res = 0;
int qs, qe;
memset( matchX, -1, sizeof(matchX) );
memset( matchY, -1, sizeof(matchY) );
memset( chkY, -1, sizeof(chkY) );
for( int i=0; i<nx; i++ )
{
if( matchX[i] == -1 ) //如果該X頂點未找到匹配點，將其放入佇列。
{
qs = qe = 0;
queue[qe++] = i;
prevX[i] = -1; //並且標記，它是路徑的起點
bool flag = 0;
while( qs<qe && !flag )
{
int u = queue[qs];
for( int v=0; v<ny&&!flag; v++ )
{
if( graph[u][v] && chkY[v]!=i ) //如果該節點與u有邊且未被訪問過
{
chkY[v] = i; //標記且將它的前一個頂點放入佇列中，也就是下次可能嘗試這個頂點看能否為它找到新的節點
queue[qe++] = matchY[v];
if( matchY[v] >= 0 )
prevX[matchY[v]] = u;
else //到達了增廣路徑的最後一站
{
flag = 1;
int d=u, e=v;
while( d!=-1 ) //一路通過prevX找到路徑的起點
{
int t = matchX[d];
matchX[d] = e;
matchY[e] = d;
d = prevX[d];
e = t;
}
}
}
}
qs++;
}
if( matchX[i] != -1 )
res++;
}
}
return res;
} 最優匹配演算法因為是專案需要，我用的是java。
Java程式碼
public class KuhnMunkres {
private int maxN, n, lenX, lenY;
private double[][] weights;
private boolean[] visitX, visitY;
private double[] lx, ly;
private double[] slack;
private int[] match;
public KuhnMunkres( int maxN )
{
this.maxN = maxN;
visitX = new boolean[maxN];
visitY = new boolean[maxN];
lx = new double[maxN];
ly = new double[maxN];
slack = new double[maxN];
match = new int[maxN];
}
public int[][] getMaxBipartie( double weight[][], double[] result )
{
if( !preProcess(weight) )
{
result[0] = 0.0;
return null;
}
//initialize memo data for class
//initialize label X and Y
Arrays.fill(ly, 0);
Arrays.fill(lx, 0);
for( int i=0; i<n; i++ )
{
for( int j=0; j<n; j++ )
{
if( lx[i]<weights[i][j])
lx[i] = weights[i][j];
}
}
//find a match for each X point
for( int u=0; u<n; u++ )
{
Arrays.fill(slack, 0x7fffffff);
while(true)
{
Arrays.fill(visitX, false);
Arrays.fill(visitY, false);
if( findPath(u) ) //if find it, go on to the next point
break;
//otherwise update labels so that more edge will be added in
double inc = 0x7fffffff;
for( int v=0; v<n; v++ )
{
if( !visitY[v] && slack[v] < inc )
inc = slack[v];
}
for( int i=0; i<n; i++ )
{
if( visitX[i] )
lx[i] -= inc;
if( visitY[i] )
ly[i] += inc;
}
}
}
result[0] = 0.0;
for( int i=0; i<n; i++ )
{
if( match[i] >= 0 )
result[0] += weights[match[i]][i];
}
return matchResult();
}
public int[][] matchResult()
{
int len = Math.min(lenX, lenY);
int[][] res = new int[len][2];
int count=0;
for( int i=0; i<lenY; i++ )
{
if( match[i] >=0 && match[i]<lenX )
{
res[count][0] = match[i];
res[count++][1] = i;
}
}
return res;
}
private boolean preProcess( double[][] weight )
{
if( weight == null )
return false;
lenX = weight.length; lenY = weight[0].length;
if( lenX>maxN || lenY>maxN )
return false;
Arrays.fill(match, -1);
n = Math.max(lenX, lenY);
weights = new double[n][n];
for( int i=0; i<n; i++ )
Arrays.fill(weights[i], 0.0);
for( int i=0; i<lenX; i++ )
for( int j=0; j<lenY; j++ )
weights[i][j] = weight[i][j];
return true;
}
private boolean findPath( int u )
{
visitX[u] = true;
for( int v=0; v<n; v++ )
{
if( !visitY[v] )
{
double temp = lx[u]+ly[v]-weights[u][v];
if( temp == 0.0 )
{
visitY[v] = true;
if( match[v] == -1 || findPath(match[v]) )
{
match[v] = u;
return true;
}
}
else
slack[v] = Math.min(slack[v], temp);
}
}
return false;
}
}