吳恩達第一門-神經網路和深度學習第二週6-10學習筆記
神經網路和深度學習第二週6-10學習筆記
6.更多導數的例子
在本節中,為上一節的導數學習提供更多的例子。在上一節中,我們複習了線性函式的求導方法,其導數值在各點中是相等的。本節以y=a^2這一二次函式為例,介紹了導數值在各點處發生變化時的求導方法。求導大家都會,y=x ^3的導數是3x ^2,y=x ^2的導數是2x,y=lnx的導數是1/x。這裡不做贅述。
7.計算圖
一個神經網路的計算,都是按照前向或反向傳播過程組織的。前向傳播過程就是從輸入到輸出的過程,將輸入通過計算得到輸出值。而後向傳播一般用來計算導數值,或者說是計算出輸出對應的各個神經元中值的梯度。在這節舉一個由輸入正向計算出輸出值的例子。

設有一個三元函式J(a,b,c)=3(a+bc),要完成該計算需要進行三個步驟,分別是u=bc,v=a+u,J=wv。將這三步填入上圖的計算圖中,藍線的傳遞方向即為正向傳播方向。將b,c值代入u第一個方框,計算u值為6,再將a,u值代入第二個方框計算出v值為11,最後將v值代入第三個方框計算出J值為33。這就是一個簡單的正向傳播的計算過程舉例。圖中的藍線為反向傳播過程,將在下一節中進行介紹。
8.使用計算圖求導數
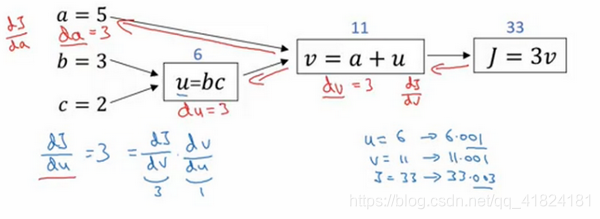
上一節介紹的是一個簡單的正向傳播過程,這一節我們對上一張配圖中的藍線過程——反向傳播過程進行舉例。我們將通過這個反向過程計算出J的各級導數。因為大家對求導都十分熟悉,這裡就不以極限的形式具體展開每一步的詳細求導過程了。根據三個方框圖,我們可以很容易地計算出J對v的導數,v對於u的導數,u對於b的導數,分別為:
根據鏈導法則:
,同理可得出:
這是一個計算流程圖,就是正向過程可以計算來計算成本函式J,如果想要優化某個函式,然後反向從右到左計算導數,對各個引數進行優化。
9.邏輯迴歸中的梯度下降
本節我們主要學習瞭如何通過計算偏導數來實現邏輯迴歸的梯度下降演算法。
回顧
首先我們先來複習一下邏輯迴歸的公式,
損失函式
其中a是邏輯迴歸的輸出,y是樣本的實際值。
梯度下降法
本節討論的單一樣本的梯度下降法應用,所以單一樣本的損失函式為

梯度下降法的目的是為了使邏輯迴歸的代價函式最小化,我們需要做的僅僅是修改w引數和b引數的值。自然而然地可以想出我們要對L(a,y)求導,最終目的是求出其對於w,b的導數。我們首先要做的就是求出L(a,y)對於a,z的導數,過程如下

在計算完成了導數之後,我們接下來需要做的就是一次次更新w1=w1-
*w1,w2=w2-
*w2,b=b-
*b
在本節中我們學習了怎樣計算導數,並且實現針了對單個訓練樣本的邏輯迴歸的梯度下降演算法。
10. m 個樣本的梯度下降
在上一節中我們學習瞭如何針對單個訓練樣本的邏輯迴歸的梯度下降演算法,本節中我們將梯度下降演算法用於多樣本中。
損失函式的公式為:
