概率圖模型（PGM），作為機器學習的重要分支，能串連起很多傳統模型，比如 NB、LR、MEM、HMM、CRF、DBN 等。本篇文章，從串連多個模型的角度，來談談 PGM，順便把這些模型回顧下。

1 Why PGM

從兩方面談談學習和使用 PGM 的必要性吧。

1.1 關係型資料

關係型資料具備下述兩個特性：

• 細粒度資料本身，提供了部分特徵，可以用於細粒度資料的分類
• 細粒度資料之間，存在的概率依賴關係，可以輔助（甚至是關鍵要素）細粒度資料的分類

例如：

• NLP 中的 POS、NER 任務，針對細粒度資料——字元——直接分類顯然不合理，考慮字元間的依賴關係，通常將細粒度資料組合為粗粒度資料——語句，然後用模型來捕捉細粒度資料之間的依賴關係
• 影象處理中的邊緣檢測任務，為利用細粒度資料——畫素——之間的相鄰資訊，通常基於粗粒度資料——影象——進行建模
• 網頁分類任務中，除了網頁內文字可以提供特徵外，網頁間的超連結關係也可以提供分類表現

現在，處理關係型資料，大家可能都習慣了使用自動化的 DL 模型，諸如 CNN 利用劃窗累積的方式 model 資料間的關係。

而，PGM 提供了一種不是那麼自動化的，處理關係型資料的強大框架。

1.2 概率模型

很多大牛推崇機器學習的概率論視角，比如 Murphy 那本 MLAPP、Uber 的 Zoubin Ghahramani 等。當然，概率模型和非概率模型之間的界限也並不是涇渭分明的，例如，SVM、KNN、Ensemble 類模型都屬於非概率模型，NB、HMM 屬於概率模型，但決策樹、LR、MEM、CRF 既可以看做非概率模型也可以看做概率模型。

但，PGM 用圖結構來視覺化資料間的概率分佈關係，是一種更直觀精緻的解釋方式。

通常認為 DL 是 PGM 的一種實現方式，由於後者具備完善的理論基礎，兩者的結合也是目前研究的一個方向，早期的成果包括 DBN、DBM 等，其中主流方式就是利用 DL 做感知，PGM 做推斷。

可見，深入淺出的瞭解下 PGM 還是很有必要的。

2 What is PGM

2.1 概率圖模型

PGM，在形式上是由圖結構組成的。圖的每個節點 node 都關聯了一個隨機變數，圖的邊 edge 則用於編碼這些隨機變數之間的關係。

圖上隨機變數的依賴關係可以是單向的也可以是雙向的，從而可以將 PGM 分類為有向無環圖模型（即貝葉斯網路），無向圖模型（即馬爾科夫網路）

所謂圖模型視角就是，可以將大量隨機變數的概率分佈，分解為 local func 的乘積形式，而每個 local func 僅依賴於少量隨機變數。

具體介紹之前，引入幾個基本概念：

• $X$ 為輸入變數集合，$Y$ 為輸出變數集合，$V=X \cup Y$ 為所有隨機變數集合，共 $K$ 個，$V_k \in V$ 為其中一個隨機變數，$v$ 為 $V$ 的一個取值，$v_k$ 為 $V_k$ 的一個取值
• 圖表示為 $G=(V,E)$ ，其中，$E$ 為邊的集合，邊在有向圖中表示兩個變數之間的因果關係
• 有向圖中，$\pi(V_k)$ 為變數 $V_k$ 在圖中所有的父節點構成的變數集合
• 無向圖中，$C$ 表示圖中的一個最大團，$V_C$ 表示其對應的隨機變數集合，其一個取值為 $v_C \in V_C$

2.2 有向圖模型（貝葉斯網路）

有向圖中，依賴關係僅存在於父子節點之間，概率分佈可分解為： $p(v)=\prod_{k=1}^{K}{p(v_k \mid \pi(v_k))}$

無向圖模型（馬爾科夫網路）

無向圖中，依賴關係通常基於全連通子圖來分割，利用 H-C 定理給出概率分解形式為： $p(v)= \frac{1}{Z} \prod_C{\psi_C(v_C)}$ 其中，partition func $Z=\sum_v{\prod_C{\psi_C(v_C)}}$ 為歸一化因子，保證概率和為1，potential func $\psi_C$ 為定義在最大團 $C$ 上的嚴格正函式。

• potential func 通常定義為 $\psi_C(v_C \mid \omega_C)=exp(\omega_C f_C(v_C))=exp{\sum_i{\omega_{Ci}} f_{Ci}(v_C)}$，其中，$f_C(v_C)$ 為定義在 $V_C$ 上的特徵向量，$\omega_C$ 為對應的權重向量，$f_{Ci}$ 為特徵函式
• partition func 的計算複雜度是指數級的，大部分演算法都是採用的近似計算

利用特徵向量，無向圖也可以表示為： $p(v)= \frac{1}{Z} exp(\sum_C {\omega_Cf_C(v_C)})$

2.3 聯絡

• 無向圖可以表示有向圖無法表示的一些依賴關係，比如迴圈依賴
• 有向圖可以表示無向圖無法表示的一些關係，比如因果關係
• 前面說的 local func，在有向圖中為可解釋的 $p(v_k \mid \pi(v_k))$，在無向圖中為沒有直接解釋的 $\psi_C(v_C)$
• 有向圖通常用來建模生成模型，無向圖通常用來建模生成模型，前者 $p(v)$ 即為 $p(x,y)$，後者通常為 $p(y \mid x)$

2.4 因子圖模型

factor graph，是一個雙向圖，表示為 $G=(V,F,E)$，其中，$\psi_C \in F$ 表示因子節點，如果變數節點 $V_k \in V$ 是 $\psi_C$ 的引數，則存在邊 $E_i \in E$ 連線兩者。

通常，無向圖和有向圖都可以更精確的表示為因子圖模型。 具體後面會舉例。

3. Examples

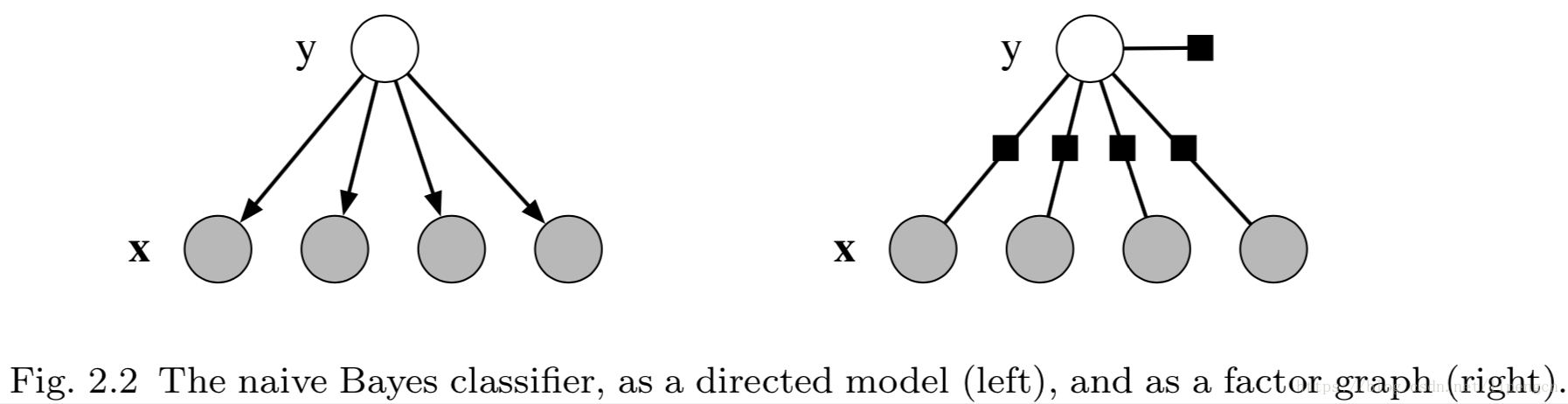
3.1 NB

NB 作為生成模型，先學習聯合概率模型，然後利用貝葉斯公式進行分類： $p(Y \mid X)=\frac{p(X,Y)}{p(X)}=\frac{p(Y)p(X|Y)}{\sum_Y{p(Y)p(X|Y)}}$

其中，聯合概率分佈形式為 $p(x,y)=p(y)\prod_i{p(x_i \mid y)}$，可以對應到有向圖模型，如下圖左圖所示。

同時，如果定義一個因子 $\psi(y)=p(y)$，針對每個特徵 $x_i$ 定義一個因子 $\psi_k(y,x_i)=p(x_i \mid y)$，就可以表示為因子圖模型了，如下圖右圖所示。

3.2 LR

LR 作為判別模型，不必去學聯合概率分佈。LR 可以理解為每個 class 的對數概率，即 $log{p(y|x)}$，是特徵向量 $x$ 的線性函式，也可以理解為條件概率分佈的形式為引數化的邏輯斯蒂分佈的概率模型，形式都為： $p(y \mid x) = \frac{1}{Z(x)}{exp(\sum_i{\omega_{{y}i}x_i})}$

引入特徵函式 $f_{y'i}(y,x)=1(y'=y)x_i$