今天要寫的部落格說簡單也簡單，是大家熟悉的線性模型，但是我們通過線性模型的不足，我們匯出嶺迴歸，下面是部落格的結構。
    1.線性模型
    2.線性模型出現的問題
    3.改進線性模型—->嶺迴歸的匯入

1.線性模型

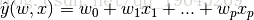
    上面的公式是大家再熟悉不過的公式了，通過優化損失函式

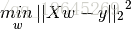
從而可以得到引數w的值。實際上上面優化的公式就相當於求解

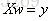
2.線性模型出現的問題
2.1 出現的問題
    你有沒有考慮過一個問題，當你選取的特徵如果存在共線性，或者逼近存在共線性的時候，會出現什麼情況呢？
    問題：普通的線性模型對噪聲非常的敏感

2.2 噪聲敏感的例子
    給大家舉個例子什麼叫對噪聲比較敏感。

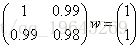
通過求解方程Aw=y可以很容易得到解

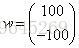
    下面給X和y都加點噪聲，對係數舉證加個擾動，然後對右端項加擾動得到方程

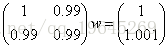
    看到沒有，只是將X和y加了一點點噪聲，和之前的方程變化並不大，但是最後的解會讓你大吃一驚。

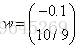
從而可以看出來普通的線性模型對於模型非常的敏感。
    這裡面實際上牽扯到的是矩陣論中非常重要的一章的內容那就是對矩陣擾動的分析。那麼怎麼樣去判斷一個矩陣對噪聲是不是很敏感呢，下面通過一個簡單的推導，如果想具體看推導的過程可以參照戴華老師的矩陣論。
    下面假設只對y進行很小的擾動
    定理：

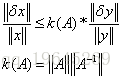
對y進行小小的擾動,不等式左側表示的是x經過y擾動後的變化情況，從不等式可以看出，當k(A)非常的時候表示，對噪聲越明顯。
    那麼為什麼上面的情況k(A)非常的大呢。
    假設我們用無窮範數來進行衡量k(A)，那麼上面的例子中，

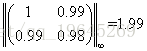
    從而可以求出k(A)=3.96*10^4,可以看出k(A)非常的大，所以對噪聲特別的敏感。
    那麼怎麼樣對A進行處理，使k(A)變小呢？

2.2 解決方式
    上面講到k(A)非常的大：對擾動非常的敏感，可以通過對A加上一個

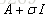
通過上方式可以降低k(A)的值
驗證：假設對上面的問題通過加上0.001E得到

從而可以算出

可以得到k(A+0.001I) = 2.089*10^3,可以看出k(A)明顯降低，當然如果將係數加大，那麼敏感度會進一步降低。

3. 改進線性模型—->嶺迴歸的匯入
那麼上面扯了那麼多，和嶺迴歸有毛關係呢。請看嶺迴歸的損失函式

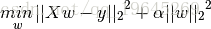
對上面的損失函式對w進行求導

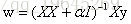
看到沒有，這樣的處理方式和上面降低敏感度的處理方式是一樣的，說明嶺迴歸模型對噪聲可以起到魯棒的作用。
    所以嶺迴歸在損失函式後面加上正則化項有以下作用：
    A: 使模型簡單。
    B:對噪聲魯棒