Problem Description

我們稱一個有向圖G是傳遞的，當且僅當對任意三個不同的頂點a,若G中有 一條邊從a到b且有一條邊從b到c ,則G中同樣有一條邊從a到c。 我們稱圖G是一個競賽圖，當且僅當它是一個有向圖且它的基圖是完全圖。換句 話說，將完全圖每條邊定向將得到一個競賽圖。 下圖展示的是一個有4個頂點的競賽圖。 現在，給你兩個有向圖P = (V,Ep)和Q = (V,Ee)，滿足: \1. EP與Ee沒有公共邊； \2. (V,Ep⋃Ee)是一個競賽圖。 你的任務是：判定是否P，Q同時為傳遞的。

Input

包含至多20組測試資料。 第一行有一個正整數，表示資料的組數。 對於每組資料，第一行有一個正整數n。接下來n行，每行為連續的n個字元，每 個字元只可能是’-’,’P’,’Q’中的一種。 ∙如果第i行的第j個字元為’P’，表示有向圖P中有一條邊從i到j; ∙如果第i行的第j個字元為’Q’，表示有向圖Q中有一條邊從i到j; ∙否則表示兩個圖中均沒有邊從i到j。 保證1 <= n <= 2016，一個測試點中的多組資料中的n的和不超過16000。保證輸入的圖一定滿足給出的限制條件。

Output

對每個資料，你需要輸出一行。如果P! Q都是傳遞的，那麼請輸出’T’。否則， 請輸出’N’ (均不包括引號)。

Sample Input

4
4
-PPP
--PQ
---Q
----
4
-P-P
--PQ
P--Q
----
4
-PPP
--QQ
----
--Q-
4
-PPP
--PQ
----
--Q-

Sample Output

T
N
T
N

Hint

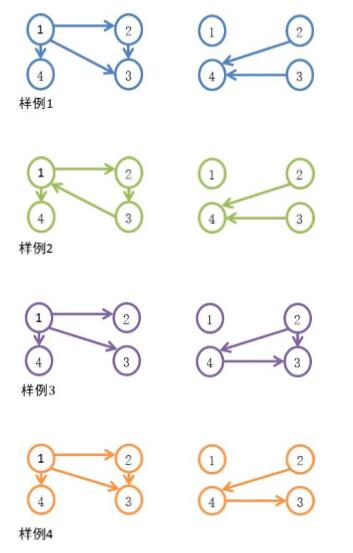
在下面的示意圖中，左圖為圖為Q。

注：在樣例2中，P不是傳遞的。在樣例4中，Q不是傳遞的。

思路

題目已經給出如何判斷一個圖是傳遞的.

當這個圖為傳遞的，兩個子圖要滿足兩個條件:

• P+Q的合圖無環
• P+Q的反圖(即Q圖重的方向改成反向)的合圖無環

使用拓撲排序判環即可

程式碼

#include <bits/stdc++.h>
using namespace std;
#define mem(a, b) memset(a, b, sizeof(a))
const int N = 2020;
vector<int> e1[N];
vector<int> e2[N];
char s[N][N];
int vis[N], n;
bool dfs1(int u)
{
    vis[u] = -1;
    for (auto v : e1[u])
    {
        if
 
 (vis[v] < 0)
            return false;
        else if (!vis[v] && !dfs1(v))
            return false;
    }
    vis[u] = 1;
    return true;
}
bool dfs2(int u)
{
    vis[u] = -1;
    for (auto v : e2[u])
    {
        if (vis[v] < 0)
            return false;
        else if (!vis[v] && !dfs2(v))
            return false;
    }
    vis[u] = 1;

    return true;
}
bool topsort1()
{

    mem(vis, 0);
    for (int u = 1; u <= n; u++)
        if (!vis[u])
            if (!dfs1(u))
                return false;
    return true;
}
bool topsort2()
{

    mem(vis, 0);
    for (int u = 1; u <= n; u++)
        if (!vis[u])
            if (!dfs2(u))
                return false;
    return true;
}
void solve()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        e1[i].clear();
        e2[i].clear();
    }
    for (int i = 1; i <= n; i++)
    {
        scanf("%s", s[i] + 1);
        for (int j = 1; j <= n; j++)
        {
            if (s[i][j] == 'P')
            {
                //puts("!!!");
                e1[i].push_back(j);
                e2[i].push_back(j);
            }
            else if (s[i][j] == 'Q')
            {
                e1[i].push_back(j);
                e2[j].push_back(i);
            }
        }
    }
    int f1 = topsort1(), f2 = topsort2();
    if (topsort1() && topsort2())
        puts("T");
    else
        puts("N");
}
int main()
{
    // freopen("in.txt", "r", stdin);
    int t;
    scanf("%d", &t);
    while (t--)
        solve();
    return 0;
}