最小生成樹問題:演算法分析 & Java 實現
一、簡介
1. 什麼是最小生成樹
將一個有權圖中的 所以頂點 都連線起來,並保證連線的邊的 總權重最小,即最小生成樹(mini spanning tree)問題。 例如,電子電路設計中,將所有元件的針腳連線在一起,且希望所使用的連線長度最短。
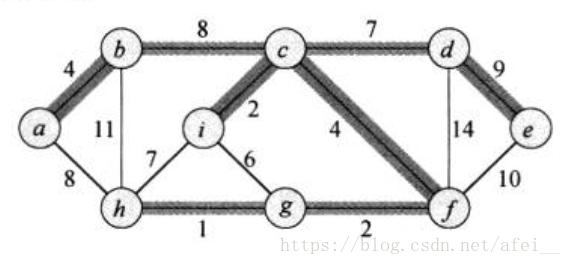
2. 圖示
二、演算法分析
1. 怎麼求解
解決最小生成樹的問題通常有兩種解法:Kruskal 演算法和 Prim 演算法。它們都屬於 貪婪演算法
2. Kruskal 演算法
第一步,我們找出 權重最短 的邊,並將邊的頂點合併到一顆樹中,例如 (g, h); 第二步,在剩餘邊中繼續找出 權重最短 的邊,並將邊的頂點合併到一顆樹中,例如 (c, i); 重複第二步,直到所有的頂點都合併到同一顆樹中。
注意,如果某條邊的兩個頂點已經在同一顆樹中了,則跳過該邊,因為加入該邊將導致閉環(它的兩個頂點已經在同一顆樹中連線了,沒必要再加這條邊了)。
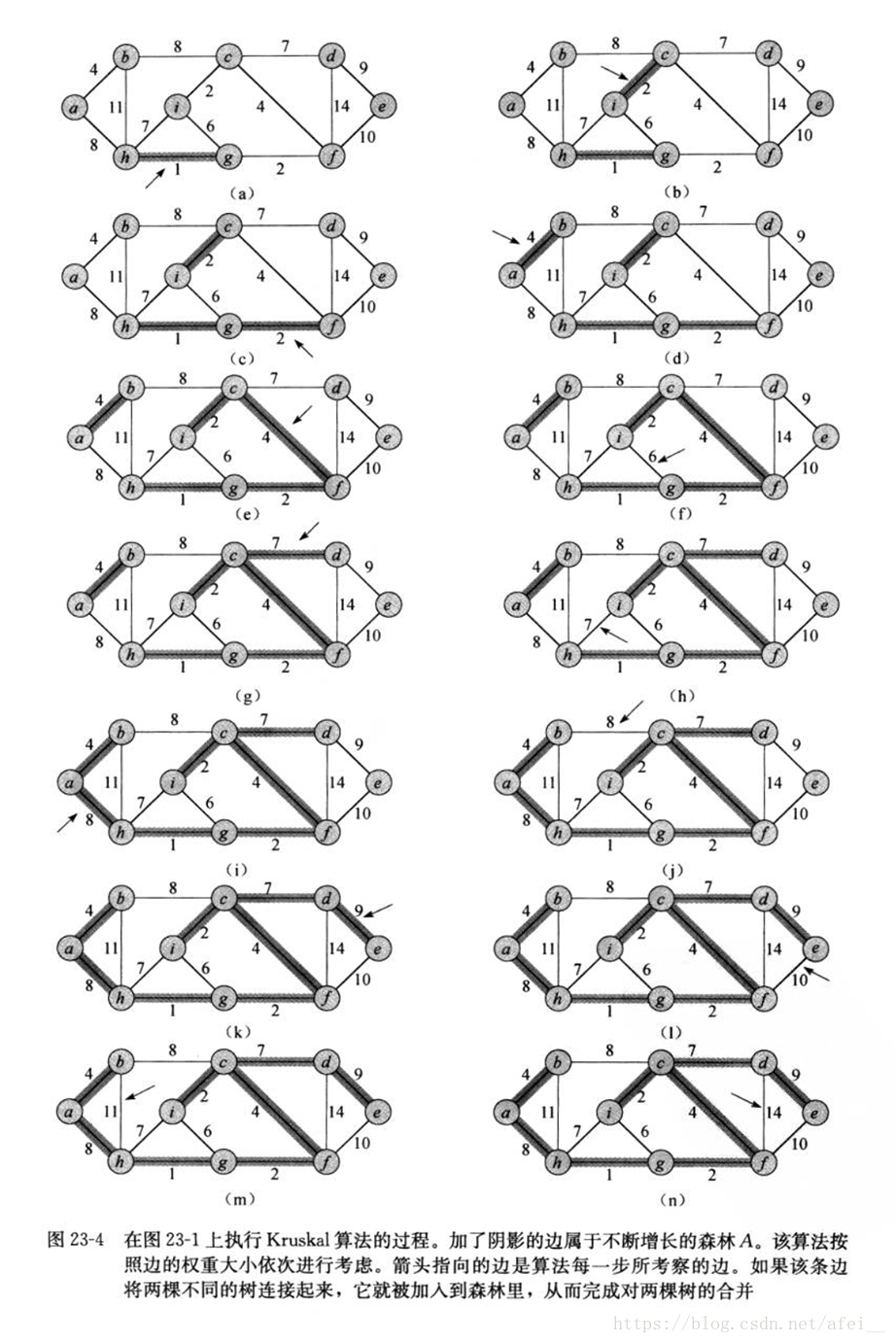
3. 過程圖解
根據上述過程,我們始終找尋當前滿足要求且權重最小的邊:
三、程式碼實現
好了,理論說了這麼多看著也乏味,關鍵是程式碼要怎麼寫呢?
1. Edge 類
我們演算法最後返回的結果其實就是一個 “邊” 的集合。我們很容易想到我們需要一個類來表示圖的邊,它應該包含兩個頂點和權重這些資訊,且之後我們需要根據邊的權重從小到大排序,所以 Edge 類還應該實現 Comparable 介面。
public class Edge implements Comparable<Edge> {
private Vertex start;
private Vertex end;
private int weight; // 權重
public Edge(Vertex start, Vertex end, 2. Vertex 類
上面 Edge 類裡有兩個頂點,這個頂點類當然也是需要的。由於演算法之後需要判斷兩個頂點是否在同一個樹中,那麼最簡單的方式就是判斷頂點目前所在的樹的根結點是否相同即可。
所以我們需要通過 Vertex 類找到樹的根結點,可以建立一個 TreeNode 類表示樹的結點,然後 Vertex 類繼承 TreeNode 類,因為頂點可以看作就是樹中的一個葉子結點。
public class Vertex extends TreeNode {
private char value; // 頂點的值
public Vertex(char value) {
this.value = value;
}
public char getValue() {
return value;
}
public TreeNode getRoot() {
TreeNode root = this;
while (root.getParent() != null) {
root = root.getParent();
}
return root;
}
public void setRoot(TreeNode treeNode) {
getRoot().setParent(treeNode);
}
}
其父類為:
public class TreeNode {
protected TreeNode parent;
public TreeNode getParent() {
return parent;
}
public void setParent(TreeNode parent) {
this.parent = parent;
}
}
3. 場景類
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Main {
public static void main(String[] args) {
List<Edge> edges = getTestData(); // 獲取測試資料
List<Edge> result = miniSpanningTree(edges); // 得到最小生成樹
printEdges(result); // 列印最小生成樹的邊
}
public static List<Edge> miniSpanningTree(List<Edge> edges) {
ArrayList<Edge> result = new ArrayList<>();
Collections.sort(edges); // 根據邊權重從小到大排序
for (Edge edge : edges) {
Vertex u = edge.getStart();
Vertex v = edge.getEnd();
// 如果 u 和 v 已經在同一顆樹裡則跳過
if (u.getRoot() == v.getRoot()) {
continue;
}
result.add(edge);
// 將 u 和 v 放在同一顆樹裡
// 合併兩個樹最直接的辦法就是使用一個新的根結點,然後連線兩個子樹
TreeNode newRoot = new TreeNode();
u.setRoot(newRoot);
v.setRoot(newRoot);
}
return result;
}
public static List<Edge> getTestData() {
ArrayList<Edge> list = new ArrayList<>();
Vertex[] vertexes = new Vertex[9];
for (int i = 0; i < vertexes.length; i++) {
// 'a' to 'i'
vertexes[i] = new Vertex((char) (i + 97));
}
list.add(new Edge(vertexes[0], vertexes[1], 4)); // a-b
list.add(new Edge(vertexes[0], vertexes[7], 8)); // a-h
list.add(new Edge(vertexes[1], vertexes[2], 8)); // b-c
list.add(new Edge(vertexes[1], vertexes[7], 11)); // b-h
list.add(new Edge(vertexes[2], vertexes[3], 7)); // c-d
list.add(new Edge(vertexes[2], vertexes[5], 4)); // c-f
list.add(new Edge(vertexes[2], vertexes[8], 2)); // c-i
list.add(new Edge(vertexes[3], vertexes[4], 9)); // d-e
list.add(new Edge(vertexes[3], vertexes[5], 14)); // d-f
list.add(new Edge(vertexes[4], vertexes[5], 10)); // e-f
list.add(new Edge(vertexes[5], vertexes[6], 2)); // f-g
list.add(new Edge(vertexes[6], vertexes[7], 1)); // g-h
list.add(new Edge(vertexes[6], vertexes[8], 6)); // g-i
list.add(new Edge(vertexes[7], vertexes[8], 7)); // h-i
return list;
}
public static void printEdges(List<Edge> edges) {
for (int i = 0; i < edges.size(); i++) {
Edge edge = edges.get(i);
System.out.println("(" + edge.getStart().getValue() + ", " + edge.getEnd().getValue() + ")");
}
}
}
4. 執行結果
(g, h)
(c, i)
(f, g)
(a, b)
(c, f)
(c, d)
(a, h)
(d, e)
省的大家往上翻了,最後這裡也貼一下圖: