單源最短路徑的迪克斯特拉(Dijkstra)演算法
阿新 • • 發佈:2018-12-30
Dijkstra演算法
1.定義概覽
Dijkstra(迪傑斯特拉)演算法是典型的單源最短路徑演算法,用於計算一個節點(節點需為源點)到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴充套件,直到擴充套件到終點為止。Dijkstra演算法是很有代表性的最短路徑演算法,注意該演算法要求圖中不存在負權邊。
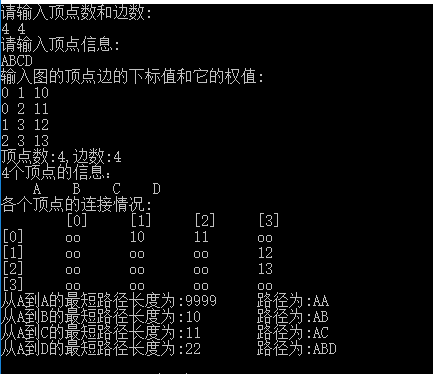
例項:假設有A,B,C,D四個城市,(這裡討論的是有向網) 它們的距離為: A->B(10),A->C(11),B->D(12),C->D(13);
所謂単源路徑就是解決從源點 A開始找出到其他城市的最短距離(除本身外的其他所有城市)。Dijkstra演算法可以求出A->B(10),A->C(11),A->D(22);
拓展2:多源最短路徑(常用Floyd演算法)是解決任意兩點間的最短路徑的一種演算法,(不侷限於從源點出發,到其他各個頂點 )可以正確處理有向圖或負權的最短路徑問題,同時也被用於計算有向圖的傳遞閉包。Floyd演算法的時間複雜度為O(N3),空間複雜度為O(N2)。
程式碼
/* @ Dijkstra演算法(単源最短路徑) */ #include<iostream> #include<cstdio> #include<cstdlib> #define MAXV 100 #define LIMITLESS 9999 //定義為無窮大,預設為節點間不存在聯絡 using namespace std; typedef struct { char info; //頂點其他資訊 }VertexType; typedef struct MGraph { int v; //頂點數 int e; //邊數 int edges[MAXV][MAXV];//鄰接矩陣的陣列表現 VertexType vexs[MAXV]; //頂點資訊 }MGraph; void creat(MGraph *G) { int i, j, k, w; int start, end; printf("請輸入頂點數和邊數:\n"); scanf("%d%d", &(G->v), &(G->e)); getchar(); printf("請輸入頂點資訊:\n"); for (i = 0; i<G->v; i++) { scanf("%c", &(G->vexs[i].info)); } for (i = 0; i<G->v; i++) { for (j = 0; j<G->v; j++) { G->edges[i][j] = LIMITLESS; } } printf("輸入圖的頂點邊的下標值和它的權值:\n"); for (k = 0; k<G->e; k++) { scanf("%d%d%d", &start, &end, &w); G->edges[start][end] = w; } } void print(MGraph *G) { int i, j; printf("頂點數:%d,邊數:%d\n", G->v, G->e); printf("%d個頂點的資訊:\n", G->v); for (i = 0; i<G->v; i++) { printf("%5c",G->vexs[i].info); } printf("\n各個頂點的連線情況:\n"); printf("\t"); for (i = 0; i<G->v; i++) { printf("[%d]\t", i); } printf("\n"); for (i = 0; i<G->v; i++) { printf("[%d]\t", i); for (j = 0; j<G->v; j++) { if (G->edges[i][j] == LIMITLESS) { printf("oo\t"); } else { printf("%d\t", G->edges[i][j]); } } printf("\n"); } } void Ppath(MGraph *g,int path[], int i, int v) //前向遞迴查詢路徑上的頂點,但不包含起點與終點的路徑值 { int k; k = path[i]; if (k == v) //無中間節點,退出 { return; } Ppath(g,path, k, v); printf("%c",g->vexs[k]); } void Dispath(MGraph *g,int dist[], int path[], int s[], int n, int v) { int i; for (i = 0; i < n; i++) { if (s[i] == 1) { printf("從%c到%c的最短路徑長度為:%d\t路徑為:", g->vexs[v], g->vexs[i], dist[i]); printf("%c",g->vexs[v]); //輸出路徑上的起點 Ppath(g,path, i, v); //輸出路徑上的中間點 printf("%c\n",g->vexs[i]); //輸出路徑上的終點 } else { printf("從%c到%c不存在路徑\n", g->vexs[v], g->vexs[i]); } } } void Dijkstra(MGraph *g, int v) { int mindis, i, j, u; int s[MAXV]; //表示這個頂點是否存入最短路線中(0表示未加入,1表示已加入) int dist[MAXV]; //表示起始點到此頂點的距離 int path[MAXV];//表示此點的上一步是哪一個頂點 for (i = 0; i < g->v; i++) { s[i] = 0; dist[i] = g->edges[v][i]; if (g->edges[v][i] < LIMITLESS) { path[i] = v; } else { path[i] = -1; } } s[v] = 1; path[v] = 0; for (i = 0; i < g->v; i++) { mindis = LIMITLESS; //mindis置最小長度初值 for (j = 0; j < g->v; j++) //選取不在s中且具有最小距離的頂點u { if (s[j] == 0 && dist[j] <mindis) { mindis = dist[j]; u = j; } } s[u] = 1; for (j = 0; j < g->v; j++) { if (s[j] == 0) { if (g->edges[u][j] < LIMITLESS&&dist[u] + g->edges[u][j] < dist[j]) { dist[j] = dist[u] + g->edges[u][j]; path[j] = u; } } } } Dispath(g ,dist, path, s, g->v, v); } int main(void) { MGraph *g; g = (MGraph *)malloc(sizeof(MGraph)); creat(g); print(g); Dijkstra(g,0); return 0; }