計數排序(counting sort)
基於比較的排序演算法的時間複雜度下限是O(nlogn),本文介紹另外一種整數排序演算法——計數排序。計數排序是一種非比較排序穩定排序演算法,它的執行效率為O(n+m),正比於數值範圍大小(n),設待排序元素個數(m),所以它只適用於n相對於m不是特別大的情況,當m>>n時尤其適合。當然對於負整數或小數以及字元排序可以進行適當的預處理將原來待排序元素對映成自然數即可。
下面看演算法:
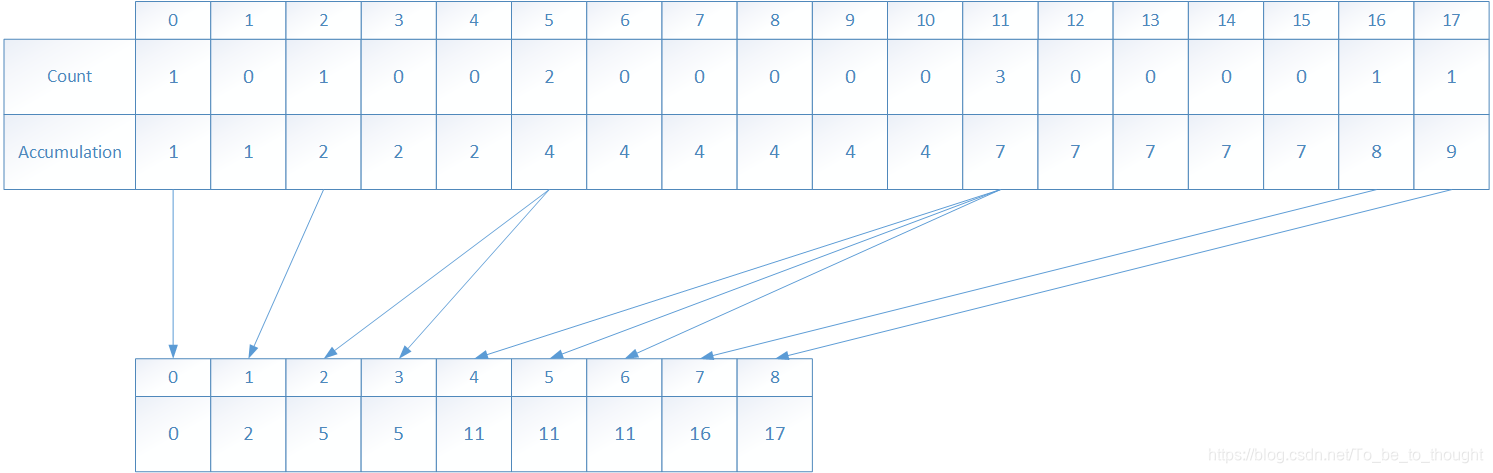
待排序元素陣列長度為9:


步驟一:計算陣列值的範圍,確定計數陣列count的長度,計數陣列的長度len=max-min+1
步驟二:遍歷原陣列,填寫計數陣列,原陣列的元素arr[i]每出現一次,以arr[i]為索引的count陣列的元素加1
步驟三:遍歷計數陣列,計算累積頻次,這個累積頻次將對應於計數陣列索引(即待排序元素)在排序後陣列中的索引位置。累積頻次(累積計數陣列元素)的意義:累積頻次(也就是該元素)總比該元素索引在排序陣列中的索引位置大1,即表示原陣列中小於等於索引值的元素數目為“累積頻次”次。
步驟四:依據計數陣列的元素值逆序填寫待排序陣列,累積計數陣列的元素值-1就是元素索引在排序陣列中的位置,將該元素放到正確位置後累積計數陣列的元素值要自減1,以便當同一元素再次出現時可以填到正確的空位上去。
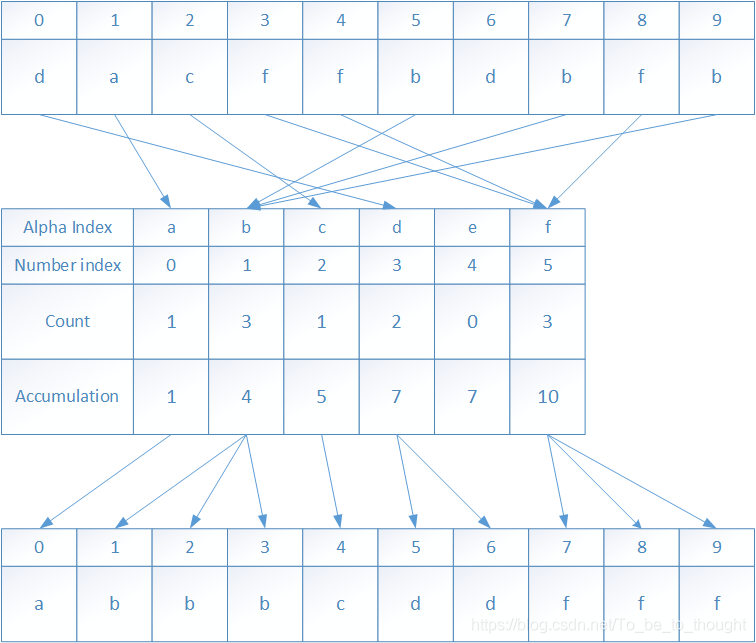
再來看一個《演算法》第四版上字元排序的例子,字串“dacffbdbfb”:

這個例子就不展開講了,主要是排序前先要進行字元到數字的對映,因為字串自身就有加減功能,所以這個對映不需要專門的函式:
下面上python程式碼:
def counting_sort(collection): if collection == []: return [] coll_len = len(collection) coll_max = max(collection) coll_min = min(collection) counting_arr_length = coll_max + 1 - coll_min counting_arr = [0] * counting_arr_length for number in collection: counting_arr[number - coll_min] += 1 for i in range(1, counting_arr_length): counting_arr[i] = counting_arr[i] + counting_arr[i-1] ordered = [0] * coll_len for i in reversed(range(0, coll_len)): ordered[counting_arr[collection[i] - coll_min]-1] = collection[i] counting_arr[collection[i] - coll_min] -= 1 return ordered
測試執行:


