Ikaros的資料結構之二叉樹(基礎概念部分)
二叉樹(Binary Tree)
在瞭解二叉樹之前你需要了解如下內容:
1.樹(Tree):是一種非線性資料結構(非線性資料結構包含樹和圖)
①樹的資料結構:

對樹狀結構的特點的總結
1.有且只有一個結點無前驅(根結點) 2.可有多個結點無後繼(葉子結點) 3.除根結點,葉子結點外:其餘結點均只有一個雙親,但可以有(包含一個)多個子女結點
接下來,我們進入正題:二叉樹
1.定義:度值最大為2的樹
2.形態:


②廣義表表示法:根節點(左子女,右子女) 仍然以Tree1為例: A(B,C) B(D,E) C(,F) D(G) E(H,I) F(J) 以上過程只是為了讀者更好的理解,接下來才是用廣義表表示法表示的結果: A(B(D(G),E(H,I)),C(,F(J))) 注:當只有左結點時,逗號可被省去;但是當只有右結點時,逗號不可省,否則會被誤以為時左結點
以上這兩種方法通常用在文件中,實際更多情況中用畫圖更多一些
4.二叉樹的性質特點 a.任意一棵非空二叉樹的葉子結點總比雙分支結點多一個 證明:(證明過程中遵循的原則:結點總個數守恆) 因為在二叉樹中,共有三類雙親結點:①有0個子女結點的雙親結點(葉子結點)②有1個子女的雙親結點③有2個子女結點的雙親結點 設有0個子女結點的雙親結點的個數為n0,有1個子女結點的雙親結點的個數為n1,有2個子女結點的雙親結點的個數為n2 若把二叉樹中的所有結點都看作雙親結點,樹中的結點總數為:n2+n1+n0
5.常見的幾種二叉樹
a.滿二叉樹
對二叉樹按層編號:0,1,2……
編號為i的層最多隻有2^i個結點(每層結點個數最大值)
若一棵h層的二叉樹的每一層的結點個數都達到最大值,則稱這棵二叉樹為滿二叉樹
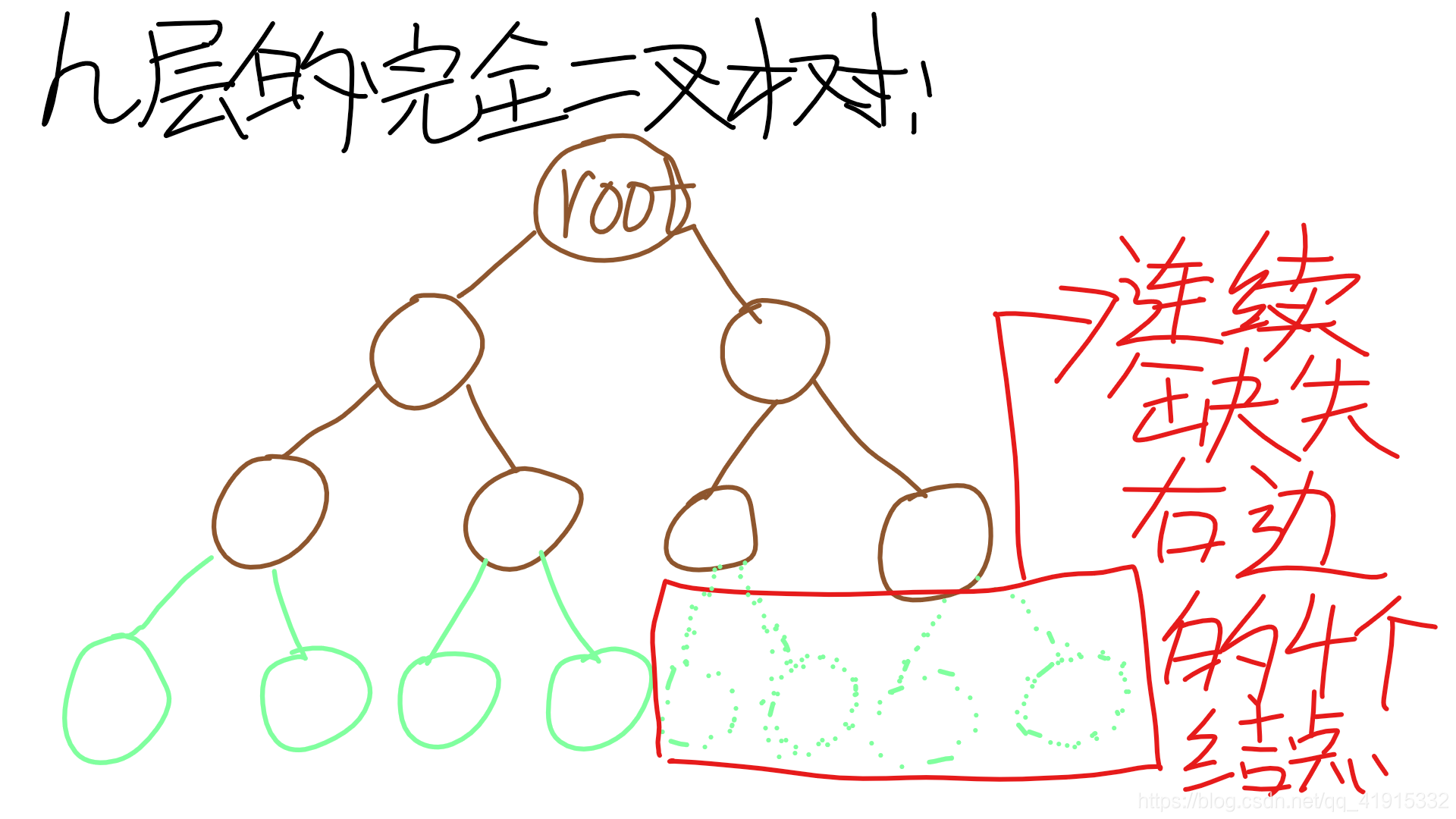
 b.完全二叉樹:一棵h層的完全二叉樹
特點:①前h-1層是滿的
②最後一層連續缺失右邊的結點(注:這裡右邊的結點並不是右子女結點,而是相對於左邊的結點而言的)
b.完全二叉樹:一棵h層的完全二叉樹
特點:①前h-1層是滿的
②最後一層連續缺失右邊的結點(注:這裡右邊的結點並不是右子女結點,而是相對於左邊的結點而言的)
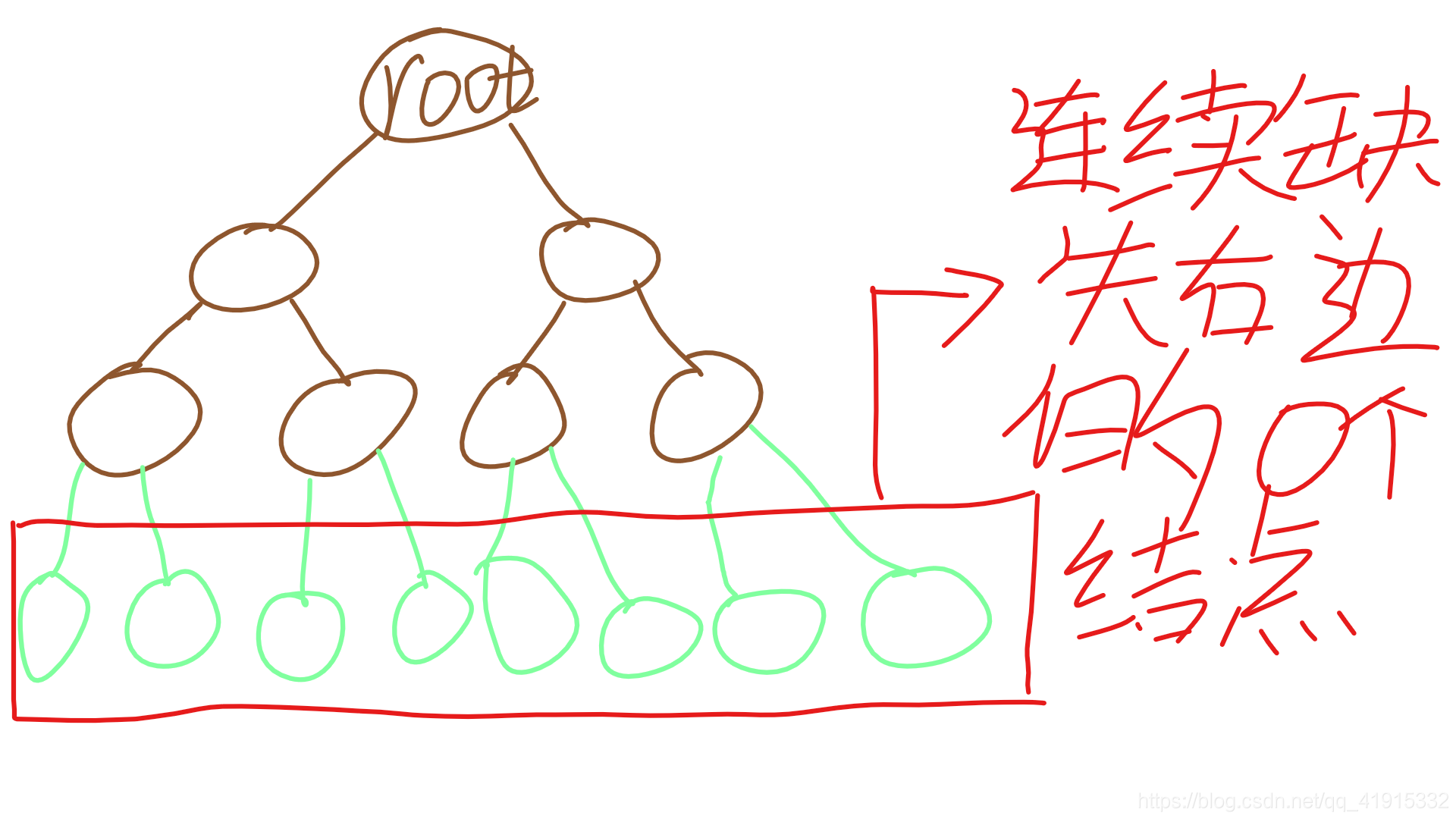
 ③ 滿二叉樹是特殊的完全二叉樹:
③ 滿二叉樹是特殊的完全二叉樹:
 ④要麼只有一個單分支結點,要麼沒有:
④要麼只有一個單分支結點,要麼沒有:
 ⑤若結點總個數為奇數,單分支結點個數為0;若n為偶數,單分支結點個數為1
⑥根據完全二叉樹的結點總個數來判斷該二叉樹的層數
設該完全二叉樹有h層,結點個數為n
則n滿足2h-1-1<n<=2h-1
即2h-1<n+1<=2h
假設該二叉樹的n=700,則210-1<700+1<=210,顯而易見,h=10,該二叉樹有10層
c.理想平衡二叉樹(理想樹)
前h-1層是滿的,最後一層隨意擺放
結論:滿二叉樹是完全二叉樹的子集,完全二叉樹為理想二叉樹的子集
d.歪斜樹:結點偏向於左邊或右邊的樹
⑤若結點總個數為奇數,單分支結點個數為0;若n為偶數,單分支結點個數為1
⑥根據完全二叉樹的結點總個數來判斷該二叉樹的層數
設該完全二叉樹有h層,結點個數為n
則n滿足2h-1-1<n<=2h-1
即2h-1<n+1<=2h
假設該二叉樹的n=700,則210-1<700+1<=210,顯而易見,h=10,該二叉樹有10層
c.理想平衡二叉樹(理想樹)
前h-1層是滿的,最後一層隨意擺放
結論:滿二叉樹是完全二叉樹的子集,完全二叉樹為理想二叉樹的子集
d.歪斜樹:結點偏向於左邊或右邊的樹
6.對任意一棵二叉樹按層從上到下,從左至右對結點進行編號(1,2,3,4,5……) 注意:對缺失的結點也要編號 則編號為i的結點若有左子女結點,那麼編號為2i;若有右子女結點,則編號為2i+1。 編號為i(i>1)的結點的雙親結點的編號為:[i/2] ([]表示對結果取整)
(。・∀・)ノ本節結束!!!
