舉一個經典的例子，社會學家經常把人按其經濟狀況分成3類：下層、中層、上層，我們用1,2,3 分別代表這三個階層。社會學家們發現決定一個人的收入階層的最重要的因素就是其父母的收入階層。如果一個人的收入屬於下層類別，那麼他的孩子屬於下層收入的概率是 0.65, 屬於中層收入的概率是 0.28, 屬於上層收入的概率是 0.07。事實上，從父代到子代，收入階層的變化的轉移概率如下

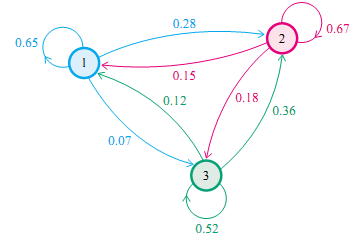
假設初始概率分佈為[0.210, 0.680, 0.110]，則我們可以計算前10代人的分佈狀況如下。

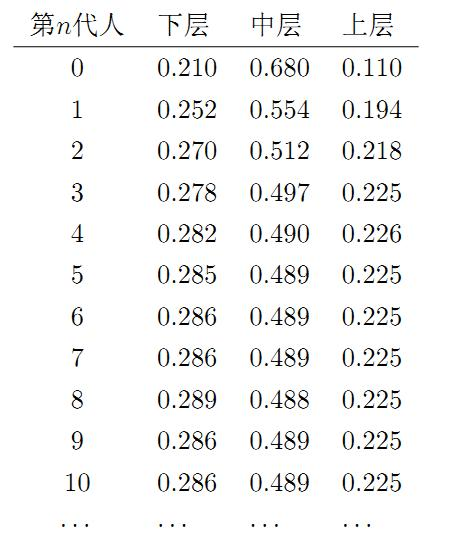
我們發現從第7代人開始，這個分佈就穩定在[0.286, 0.489, 0.225]，這個是偶然的嗎？我們換一個初始概率分佈[0.75, 0.15, 0.1]，試試看，繼續計算前代人的分佈狀況如下

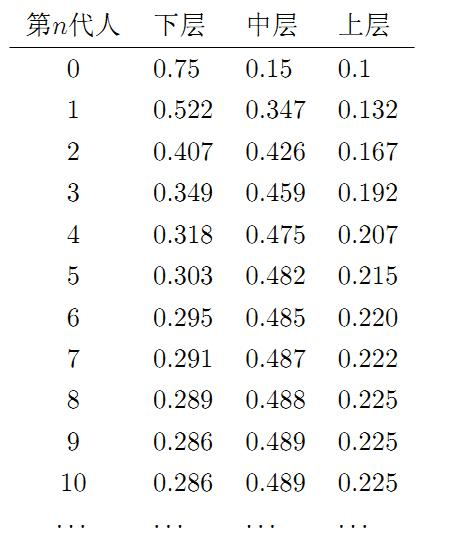
從第9代人開始，這個分佈就穩定在[0.286, 0.489, 0.225]。不管從哪一個初始分佈[0.210, 0.680, 0.110]或者[0.75, 0.15, 0.1]開始，轉移多次後就能達到平穩不變的分佈[0.286, 0.489, 0.225]。

因此，馬爾科夫的穩定分佈與初始分佈無關，只與轉移概率矩陣有關。

在轉移概率矩陣P作用下達到的平穩分佈$\pi(x)$，我們稱之為馬氏鏈平穩分佈，有如下定理：

任意兩個狀態連通並非指狀態i可以一步轉移到j，而是指狀態i可以通過有限的次數轉移到j。

1. 狀態轉移矩陣自乘多次轉移後，會得到一個穩定值

2. 馬氏鏈穩定後，所有狀態i轉移到狀態j的概率之和是穩定的

3. 一個狀態轉移矩陣只有唯一一個對應的穩定分佈$\pi(x)$

細緻平穩條件：

如果非週期馬爾科夫鏈的狀態轉移矩陣P和概率分佈$\pi(x)$對於所有的$i,j$滿足：

則稱概率分佈$\pi(x)$是狀態轉移矩陣P的平穩分佈。

證明：

$\begin{array}{l}
\sum\limits_{i = 0}^\infty {\pi (i)P(i,j)} = \sum\limits_{j = 0}^\infty {\pi (j)P(j,i)} \\
\pi (j) = \pi (j)\sum\limits_{j = 0}^\infty {P(j,i)}
\end{array}$

也就是

$\pi P = \pi $

需要注意的是這是一個充分條件，而不是必要條件，也就是說存在具有平穩分佈的馬爾科夫鏈不滿足此細緻平衡條件。