基於圖的推薦演算法及Python實現（PersonalRank）
阿新 • • 發佈：2018-12-17
使用隨機遊走演算法PersonalRank實現基於圖的推薦。
二部圖
在推薦系統中，使用者行為資料可以表示成圖的形式，具體來說是二部圖。使用者的行為資料集由一個個（u,i）二元組組成，表示為使用者u對物品i產生過行為。本文中我們認為使用者對他產生過行為的物品的興趣度是一樣的，也就是我們只考慮“感興趣”OR“不感興趣”。假設有下圖所示的行為資料集。
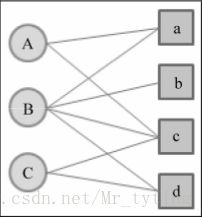
其中，users集U={A, B, C}，items集I = {a,b,c,d}。則使用者物品的二部圖為：
圖中頂點的相關度主要取決與以下因素：
1）兩個頂點之間路徑數
2）兩個頂點之間路徑長度
3）兩個頂點之間路徑經過的頂點
而相關性高的頂點一般有如下特性：
PersonalRank
假設給使用者u進行個性化推薦，從圖中使用者u對應的節點vu開始遊走，遊走到一個節點時，首先按照概率alpha決定是否繼續遊走，還是停止這次遊走並從vu節點開始重新遊走。如果決定繼續遊走，那麼就從當前節點指向的節點中按照均勻分佈隨機選擇一個節點作為下次經過的節點，這樣經過很多次的隨機遊走後，每個物品節點被訪問到的概率就會收斂到一個數。最終推薦列表中物品的權重就是物品節點的訪問概率。
將上述介紹轉換為公式得：
公式中PR(i)表示物品i的訪問概率(也即是物品i的權重)，out(i)表示物品節點i的出度。alpha決定繼續訪問的概率。
python實現（User，Item）二分圖
以下面的二分圖為例，實現PersonalRank演算法：
import time import operator def PersonalRank(G, alpha, root, max_depth): rank = dict() rank = {x : 0 for x in G.keys()} rank[root] = 1 #開始迭代 begin = time.time() for k in range(max_depth): tmp = {x : 0 for x in G.keys()} #取出節點i和他的出邊尾節點集合ri for i, ri in G.items(): #取節點i的出邊的尾節點j以及邊E(i,j)的權重wij,邊的權重都為1 for j, wij in ri.items(): #i是j的其中一條入邊的首節點，因此需要遍歷圖找到j的入邊的首節點， #這個遍歷過程就是此處的2層for迴圈，一次遍歷就是一次遊走 tmp[j] += alpha * rank[i] / (1.0 * len(ri)) #我們每次遊走都是從root節點出發，因此root節點的權重需要加上(1 - alpha) tmp[root] += (1 - alpha) rank = tmp #輸出每次迭代後各個節點的權重 print （'iter: ' + str(k) + "\t"） for key, value in rank.items(): print （"%s:%.3f, \t"%(key, value)） print('\n') end = time.time() print('use_time', end-begin) lst = sorted(rank.items(), key =operator.itemgetter(1), reverse=True) for ele in lst: print ("%s:%.3f, \t" %(ele[0],ele[1])) return rank
if __name__=='__main__':
alpha=0.8
G = {'A': {'a': 1, 'c': 1},
'B': {'a': 1, 'b': 1, 'c': 1, 'd': 1},
'C': {'c': 1, 'd': 1},
'a': {'A': 1, 'B': 1},
'b': {'B': 1},
'c': {'A': 1, 'B': 1, 'C': 1},
'd': {'B': 1, 'C': 1}}
PersonalRank(G,alpha,'b',50)
上面的程式碼是對本文一開始描述的資料集中的使用者A進行推薦。上圖給出了不同迭代次數後各節點的概率值。發現46次迭代之後，所有節點的概率值全都收斂。在這個例子中，A使用者沒有產生過行為的物品是b和d，相對於A的訪問概率分別是0.039,0.076，d的訪問概率顯然要大於b，所有給A使用者的推薦列表為{d,b}。
上面演算法在時間複雜度上有個明顯的缺陷，每次為每個使用者推薦時，都需要在整個使用者物品二分圖上進行迭代，直到整個圖上每個節點收斂。這一過程時間複雜度非常高，不僅無法提高實時推薦，甚至離線生產推薦結果也很耗時。
python實現（User，Item，Tag）三分圖
比如我利用標籤來設計基於圖的推薦演算法，資料來源結構(user,item,tag),在設計使用者物品標籤三分圖時，三分圖的結構如下：
其中A,B,C是使用者，a,b,c是物品，1,2,3是標籤。使用者和物品通過標籤相連。初始是使用者和物品的邊的權重為1，如果使用者節點和物品節點通過標籤已經相連，那麼邊的權重就加1。而上面的二分圖邊權重全是1。
基於圖的演算法中，使用者對物品的興趣公式如下：
下面是利用標籤的基於PersonalRank演算法程式碼：
import numpy as np
import pandas as pd
import math
import time
import random
def genData():
data=pd.read_csv('test1/200509',header=None,sep='\t')
data.columns=['date','user','item','label']
data.drop('date',axis=1,inplace=True)
data=data[:5000]
print "genData successed!"
return data
def getUItem_label(data):
UI_label=dict()
for i in range(len(data)):
lst=list(data.iloc[i])
user=lst[0]
item=lst[1]
label=lst[2]
addToMat(UI_label,(user,item),label)
print "UI_label successed!"
return UI_label
def addToMat(d,x,y):
d.setdefault(x,[ ]).append(y)
def SplitData(Data,M,k,seed):
'''
劃分訓練集和測試集
:param data:傳入的資料
:param M:測試集佔比
:param k:一個任意的數字，用來隨機篩選測試集和訓練集
:param seed:隨機數種子，在seed一樣的情況下，其產生的隨機數不變
:return:train:訓練集 test：測試集，都是字典，key是使用者id,value是電影id集合
'''
data=Data.keys()
test=[]
train=[]
random.seed(seed)
# 在M次實驗裡面我們需要相同的隨機數種子，這樣生成的隨機序列是相同的
for user,item in data:
if random.randint(0,M)==k:
# 相等的概率是1/M，所以M決定了測試集在所有資料中的比例
# 選用不同的k就會選定不同的訓練集和測試集
for label in Data[(user,item)]:
test.append((user,item,label))
else:
for label in Data[(user, item)]:
train.append((user,item,label))
print "splitData successed!"
return train,test
def getTU(user,test,N):
items=set()
for user1,item,tag in test:
if user1!=user:
continue
if user1==user:
items.add(item)
return list(items)
def new_getTU(user,test,N):
user_items=dict()
for user1,item,tag in test:
if user1!=user:
continue
if user1==user:
if (user,item) not in user_items:
user_items.setdefault((user,item),1)
else:
user_items[(user,item)]+=1
testN=sorted(user_items.items(), key=lambda x: x[1], reverse=True)[0:N]
items=[]
for i in range(len(testN)):
items.append(testN[i][0][1])
#if len(items)==0:print "TU is None"
return items
def Recall(train,test,G,alpha,max_depth,N,user_items):
'''
:param train: 訓練集
:param test: 測試集
:param N: TopN推薦中N數目
:param k:
:return:返回召回率
'''
hit=0# 預測準確的數目
totla=0# 所有行為總數
for user,item,tag in train:
tu=getTU(user,test,N)
rank=GetRecommendation(G,alpha,user,max_depth,N,user_items)
for item in rank:
if item in tu:
hit+=1
totla+=len(tu)
print "Recall successed!",hit/(totla*1.0)
return hit/(totla*1.0)
def Precision(train,test,G,alpha,max_depth,N,user_items):
'''
:param train:
:param test:
:param N:
:param k:
:return:
'''
hit=0
total=0
for user, item, tag in train:
tu = getTU(user, test, N)
rank = GetRecommendation(G,alpha,user,max_depth,N,user_items)
for item in rank:
if item in tu:
hit += 1
total += N
print "Precision successed!",hit / (total * 1.0)
return hit / (total * 1.0)
def Coverage(train,G,alpha,max_depth,N,user_items):
'''
計算覆蓋率
:param train:訓練集 字典user->items
:param test: 測試機 字典 user->items
:param N: topN推薦中N
:param k:
:return:覆蓋率
'''
recommend_items=set()
all_items=set()
for user, item, tag in train:
all_items.add(item)
rank=GetRecommendation(G,alpha,user,max_depth,N,user_items)
for item in rank:
recommend_items.add(item)
print "Coverage successed!",len(recommend_items)/(len(all_items)*1.0)
return len(recommend_items)/(len(all_items)*1.0)
def Popularity(train,G,alpha,max_depth,N,user_items):
'''
計算平均流行度
:param train:訓練集 字典user->items
:param test: 測試機 字典 user->items
:param N: topN推薦中N
:param k:
:return:覆蓋率
'''
item_popularity=dict()
for user, item, tag in train:
if item not in item_popularity:
item_popularity[item]=0
item_popularity[item]+=1
ret=0
n=0
for user, item, tag in train:
rank= GetRecommendation(G,alpha,user,max_depth,N,user_items)
for item in rank:
if item!=0 and item in item_popularity:
ret+=math.log(1+item_popularity[item])
n+=1
if n==0:return 0.0
ret/=n*1.0
print "Popularity successed!",ret
return ret
def CosineSim(item_tags,item_i,item_j):
ret=0
for b,wib in item_tags[item_i].items():
if b in item_tags[item_j]:
ret+=wib*item_tags[item_j][b]
ni=0
nj=0
for b,w in item_tags[item_i].items():
ni+=w*w
for b,w in item_tags[item_j].items():
nj+=w*w
if ret==0:
return 0
return ret/math.sqrt(ni*nj)
def Diversity(train,G,alpha,max_depth,N,user_items,item_tags):
ret=0.0
n=0
for user, item, tag in train:
rank = GetRecommendation(G,alpha,user,max_depth,N,user_items)
for item1 in rank:
for item2 in rank:
if item1==item2:
continue
else:
ret+=CosineSim(item_tags,item1,item2)
n+=1
print "Diversity successed!",ret /(n*1.0)
return ret /(n*1.0)
def buildGrapha(record):
graph=dict()
user_tags = dict()
tag_items = dict()
user_items = dict()
item_tags = dict()
for user, item, tag in record:
if user not in graph:
graph[user]=dict()
if item not in graph[user]:
graph[user][item]=1
else:
graph[user][item]+=1
if item not in graph:
graph[item]=dict()
if user not in graph[item]:
graph[item][user]=1
else:
graph[item][user]+=1
if user not in user_items:
user_items[user]=dict()
if item not in user_items[user]:
user_items[user][item]=1
else:
user_items[user][item]+=1
if user not in user_tags:
user_tags[user]=dict()
if tag not in user_tags[user]:
user_tags[user][tag]=1
else:
user_tags[user][tag]+=1
if tag not in tag_items:
tag_items[tag]=dict()
if item not in tag_items[tag]:
tag_items[tag][item]=1
else:
tag_items[tag][item]+=1
if item not in item_tags:
item_tags[item]=dict()
if tag not in item_tags[item]:
item_tags[item][tag]=1
else:
item_tags[item][tag]+=1
return graph,user_items,user_tags,tag_items,item_tags
def GetRecommendation(G,alpha,root,max_depth,N,user_items):
rank=dict()
rank={x:0 for x in G.keys()}
rank[root]=1
#開始迭代
for k in range(max_depth):
tmp={x:0 for x in G.keys()}
#取出節點i和他的出邊尾節點集合ri
for i,ri in G.items():
#取節點i的出邊的尾節點j以及邊E(i,j)的權重wij,邊的權重都為1，歸一化後就是1/len(ri)
for j,wij in ri.items():
tmp[j]+=alpha*rank[i]*(wij/(1.0*len(ri)))
tmp[root]+=(1-alpha)
rank=tmp
lst=sorted(rank.items(),key=lambda x:x[1],reverse=True)
items=[]
for i in range(N):
item=lst[i][0]
if '/' in item and item not in user_items[root]:
items.append(item)
return items
def evaluate(train,test,G,alpha,max_depth,N,user_items,item_tags):
##計算一系列評測標準
recall=Recall(train,test,G,alpha,max_depth,N,user_items)
precision=Precision(train,test,G,alpha,max_depth,N,user_items)
coverage=Coverage(train,G,alpha,max_depth,N,user_items)
popularity=Popularity(train,G,alpha,max_depth,N,user_items)
diversity=Diversity(train,G,alpha,max_depth,N,user_items,item_tags)
return recall,precision,coverage,popularity,diversity
if __name__=='__main__':
data=genData()
UI_label = getUItem_label(data)
(train, test) = SplitData(UI_label, 10, 5, 10)
N=20;max_depth=50;alpha=0.8
G, user_items, user_tags, tag_items, item_tags=buildGrapha(train)
recall, precision, coverage, popularity, diversity=evaluate(train,test,G,alpha,max_depth,N,user_items,item_tags)
問題來了
基於逐步迭代方式的PersonalRank演算法時間複雜度太高，運算太慢太耗時。
為了解決時間複雜度過高問題，我們有兩種方案：
方案一：減少迭代次數，在收斂前就停止迭代，雖然會對精度有影響，但影響不大。
方案二：我們可以從矩陣角度出發，personalrank經過多次的迭代遊走，使得各節點的重要度趨於穩定，實際上我們根據狀態轉移矩陣：
經過一次矩陣運算就可以直接得到系統的穩態。上面迭代公式的矩陣表示形式為：
r = (1 - alpha)r0 + alphaMT r
變形為： r = (1 - alpha)(1-alphaMT)-1r0
只需計算一次 (1-alphaMT)-1，這就相當於解線性方程組了。
因為M是稀疏矩陣，我們可以利用scipy.sparse中的gmres，csr_matrix解稀疏矩陣的線性方程組。
演算法改進後python實現（User，Item）二分圖
二分圖為例，利用PersonalRank的矩陣法求解，詳細程式碼如下：
import numpy as np
from numpy.linalg import solve
import time
from scipy.sparse.linalg import gmres,lgmres
from scipy.sparse import csr_matrix
if __name__=='__main__':
alpha=0.8
vertex=['A','B','C','a','b','c','d']
M=np.matrix([[0, 0, 0, 0.5, 0, 0.5, 0],
[0, 0, 0, 0.25, 0.25, 0.25, 0.25],
[0, 0, 0, 0, 0, 0.5, 0.5],
[0.5, 0.5, 0, 0, 0, 0, 0],
[0, 1.0, 0, 0, 0, 0, 0],
[0.333, 0.333, 0.333, 0, 0, 0, 0],
[0, 0.5, 0.5, 0, 0, 0, 0]])
r0=np.matrix([[0],[0],[0],[0],[1],[0],[0]])#從'b'開始遊走
print r0.shape
n=M.shape[0]
#直接解線性方程法
A=np.eye(n)-alpha*M.T
b=(1-alpha)*r0
begin=time.time()
r=solve(A,b)
end=time.time()
print 'user time',end-begin
rank={}
for j in xrange(n):
rank[vertex[j]]=r[j]
li=sorted(rank.items(),key=lambda x:x[1],reverse=True)
for ele in li:
print "%s:%.3f,\t" %(ele[0],ele[1])
#採用CSR法對稀疏矩陣進行壓縮儲存，然後解線性方程
data=list()
row_ind=list()
col_ind=list()
for row in xrange(n):
for col in xrange(n):
if (A[row,col]!=0):
data.append(A[row,col])
row_ind.append(row)
col_ind.append(col)
AA=csr_matrix((data,(row_ind,col_ind)),shape=(n,n))
begin=time.time()
r=gmres(AA,b,tol=1e-08,maxiter=1)[0]
end=time.time()
print "user time",end-begin
rank={}
for j in xrange(n):
rank[vertex[j]]=r[j]
li=sorted(rank.items(),key=lambda x:x[1],reverse=True)
for ele in li:
print "%s:%.3f,\t" % (ele[0], ele[1])
執行結果可知，利用稀疏矩陣的線性方程解法很快就能得出結果，不需要一步步迭代。 上面程式碼有個瑕疵，就是每次手動的寫M矩陣，很不自動化。
演算法改進後python實現（User，Item，Tag）三分圖
三分圖中，利用PersonalRank的矩陣解法求解r，資料來源和上面的三分圖一樣，邊的權重也是如上面三分圖那樣定義：詳細程式碼如下
import numpy as np
import pandas as pd
import math
import random
from scipy.sparse.linalg import gmres,lgmres
from scipy.sparse import csr_matrix
def genData():
data=pd.read_csv('test1/200509',header=None,sep='\t')
data.columns=['date','user','item','label']
data.drop('date',axis=1,inplace=True)
data=data[:10000]
print "genData successed!"
return data
def getUItem_label(data):
UI_label=dict()
for i in range(len(data)):
lst=list(data.iloc[i])
user=lst[0]
item=lst[1]
label=lst[2]
addToMat(UI_label,(user,item),label)
print "UI_label successed!"
return UI_label
def addToMat(d,x,y):
d.setdefault(x,[ ]).append(y)
def SplitData(Data,M,k,seed):
'''
劃分訓練集和測試集
:param data:傳入的資料
:param M:測試集佔比
:param k:一個任意的數字，用來隨機篩選測試集和訓練集
:param seed:隨機數種子，在seed一樣的情況下，其產生的隨機數不變
:return:train:訓練集 test：測試集，都是字典，key是使用者id,value是電影id集合
'''
data=Data.keys()
test=[]
train=[]
random.seed(seed)
# 在M次實驗裡面我們需要相同的隨機數種子，這樣生成的隨機序列是相同的
for user,item in data:
if random.randint(0,M)==k:
# 相等的概率是1/M，所以M決定了測試集在所有資料中的比例
# 選用不同的k就會選定不同的訓練集和測試集
for label in Data[(user,item)]:
test.append((user,item,label))
else:
for label in Data[(user, item)]:
train.append((user,item,label))
print "splitData successed!"
return train,test
def getTU(user,test,N):
items=set()
for user1,item,tag in test:
if user1!=user:
continue
if user1==user:
items.add(item)
return list(items)
def new_getTU(user,test,N):
for user1,item,tag in test:
if user1!=user:
continue
if user1==user:
if (user,item) not in user_items:
user_items.setdefault((user,item),1)
else:
user_items[(user,item)]+=1
testN=sorted(user_items.items(), key=lambda x: x[1], reverse=True)[0:N]
items=[]
for i in range(len(testN)):
items.append(testN[i][0][1])
#if len(items)==0:print "TU is None"
return items
def Recall(train,test,AA,M,G,alpha,N,user_items):
'''
:param train: 訓練集
:param test: 測試集
:param N: TopN推薦中N數目
:param k:
:return:返回召回率
'''
hit=0# 預測準確的數目
totla=0# 所有行為總數
for user,item,tag in train:
tu=getTU(user,test,N)
rank=GetRecommendation(AA,M,G,alpha,user,N,user_items)
for item in rank:
if item in tu:
hit+=1
totla+=len(tu)
print "Recall successed!",hit/(totla*1.0)
return hit/(totla*1.0)
def Precision(train,test,AA,M,G,alpha,N,user_items):
'''
:param train:
:param test:
:param N:
:param k:
:return:
'''
hit=0
total=0
for user, item, tag in train:
tu = getTU(user, test, N)
rank =GetRecommendation(AA,M,G,alpha,user,N,user_items)
for item in rank:
if item in tu:
hit += 1
total += N
print "Precision successed!",hit / (total * 1.0)
return hit / (total * 1.0)
def Coverage(train,AA,M,G,alpha,N,user_items):
'''
計算覆蓋率
:param train:訓練集 字典user->items
:param test: 測試機 字典 user->items
:param N: topN推薦中N
:param k:
:return:覆蓋率
'''
recommend_items=set()
all_items=set()
for user, item, tag in train:
all_items.add(item)
rank=GetRecommendation(AA,M,G,alpha,user,N,user_items)
for item in rank:
recommend_items.add(item)
print "Coverage successed!",len(recommend_items)/(len(all_items)*1.0)
return len(recommend_items)/(len(all_items)*1.0)
def Popularity(train,AA,M,G,alpha,N,user_items):
'''
計算平均流行度
:param train:訓練集 字典user->items
:param test: 測試機 字典 user->items
:param N: topN推薦中N
:param k:
:return:覆蓋率
'''
item_popularity=dict()
for user, item, tag in train:
if item not in item_popularity:
item_popularity[item]=0
item_popularity[item]+=1
ret=0
n=0
for user, item, tag in train:
rank= GetRecommendation(AA,M,G,alpha,user,N,user_items)
for item in rank:
if item!=0 and item in item_popularity:
ret+=math.log(1+item_popularity[item])
n+=1
if n==0:return 0.0
ret/=n*1.0
print "Popularity successed!",ret
return ret
def CosineSim(item_tags,item_i,item_j):
ret=0
for b,wib in item_tags[item_i].items():
if b in item_tags[item_j]:
ret+=wib*item_tags[item_j][b]
ni=0
nj=0
for b,w in item_tags[item_i].items():
ni+=w*w
for b,w in item_tags[item_j].items():
nj+=w*w
if ret==0:
return 0
return ret/math.sqrt(ni*nj)
def Diversity(train,AA,M,G,alpha,N,item_tags,user_items):
ret=0.0
n=0
for user, item, tag in train:
rank = GetRecommendation(AA,M,G,alpha,user,N,user_items)
for item1 in rank:
for item2 in rank:
if item1==item2:
continue
else:
ret+=CosineSim(item_tags,item1,item2)
n+=1
print "Diversity successed!",ret /(n*1.0)
return ret /(n*1.0)
def buildGrapha(record):
graph=dict()
user_tags = dict()
tag_items = dict()
user_items = dict()
item_tags = dict()
for user, item, tag in record:
if user not in graph:
graph[user]=dict()
if item not in graph[user]:
graph[user][item]=1
else:
graph[user][item]+=1
if item not in graph:
graph[item]=dict()
if user not in graph[item]:
graph[item][user]=1
else:
graph[item][user]+=1
if user not in user_items:
user_items[user]=dict()
if item not in user_items[user]:
user_items[user][item]=1
else:
user_items[user][item]+=1
if user not in user_tags:
user_tags[user]=dict()
if tag not in user_tags[user]:
user_tags[user][tag]=1
else:
user_tags[user][tag]+=1
if tag not in tag_items:
tag_items[tag]=dict()
if item not in tag_items[tag]:
tag_items[tag][item]=1
else:
tag_items[tag][item]+=1
if item not in item_tags:
item_tags[item]=dict()
if tag not in item_tags[item]:
item_tags[item][tag]=1
else:
item_tags[item][tag]+=1
print "buildGrapha successed!"
return graph,user_items,user_tags,tag_items,item_tags
def buildMatrix_M(G):
M=[]
for key in G.keys():
lst = []
key_out = len(G[key])
for key1 in G.keys():
if key1 in G[key]:
w=G[key][key1]
lst.append(w/(1.0*key_out))
else:
lst.append(0)
M.append(lst)
print "buildMatrix_M successed!"
return np.matrix(M)
def before_GetRec(M):
n = M.shape[0]
A = np.eye(n) - alpha * M.T
data = list()
row_ind = list()
col_ind = list()
for row in xrange(n):
for col in xrange(n):
if (A[row, col] != 0):
data.append(A[row, col])
row_ind.append(row)
col_ind.append(col)
AA = csr_matrix((data, (row_ind, col_ind)), shape=(n, n))
print "before_GetRec successed!"
return AA
def GetRecommendation(AA,M,G,alpha,root,N,user_items):
items=[]
vertex=G.keys()
index=G.keys().index(root)
n = M.shape[0]
zeros=np.zeros((n,1))
zeros[index][0]=1
r0=np.matrix(zeros)
b = (1 - alpha) * r0
r = gmres(AA, b, tol=1e-08, maxiter=1)[0]
rank = {}
for j in xrange(n):
rank[vertex[j]] = r[j]
li = sorted(rank.items(), key=lambda x: x[1], reverse=True)
for i in range(N):
item=li[i][0]
if '/' in item and item not in user_items[root]:
items.append(item)
return items
def evaluate(train,test,AA,M,G,alpha,N,item_tags,user_items):
##計算一系列評測標準
recall=Recall(train,test,AA,M,G,alpha,N,user_items)
precision=Precision(train,test,AA,M,G,alpha,N,user_items)
coverage=Coverage(train,AA,M,G,alpha,N,user_items)
popularity=Popularity(train,AA,M,G,alpha,N,user_items)
diversity=Diversity(train,AA,M,G,alpha,N,item_tags,user_items)
return recall,precision,coverage,popularity,diversity
if __name__=='__main__':
data=genData()
UI_label = getUItem_label(data)
(train, test) = SplitData(UI_label, 10, 5, 10)
N=20;max_depth=50;alpha=0.8
G, user_items, user_tags, tag_items, item_tags=buildGrapha(train)
M=buildMatrix_M(G)
AA=before_GetRec(M)
recall, precision, coverage, popularity, diversity=evaluate(train, test, AA, M, G, alpha, N, item_tags, user_items)