凸包問題的Graham-Scan演算法及python實現
阿新 • • 發佈:2018-12-26
基於 Graham-Scan 的凸包求解演算法是在列舉三角形時,採用了更精細的方式,將P_0作為極點,通過極角大小定位最右下側的三角形∆P_0 P_1 P_2,然後讓三角形繞P_0點旋轉,掃描所有輸入點,直到到最左下側為止。
首先要對點集S進行預處理,選縱座標最小的點作為P_0,其餘點在以P_0為極點、水平方向為極軸的極座標系下按極角從小到大排序。
Graham-Scan 演算法的虛擬碼如下:
Graham-Scan(S):
輸入:平面n個點的集合S,經預處理後儲存於P[0:m]
輸出:S的凸包Q
If m<=1
Then 返回“凸包為空”
將P[0]、P[1]、P[2]依次壓入棧Q
For 隨機點集S生成部分與蠻力演算法相同
對點集S的預處理中,使用氣泡排序來比較兩點極角大小,並將極角由小到大排序,在兩點的極角相等時,保留距離P_0最遠的點,刪除另一個點。實現程式碼如下所示:
#氣泡排序來比較極角大小,將極角由小到大排序
def bubble_sort(array,p0,temp):
for i in range(len(array)-1):
#current_status是用來判斷冒泡是否結束
current_status = False 接下來是演算法的主程式部分,程式碼如下:
def scan(lis,n):
starttime = datetime.datetime.now()
Q = []
lis_scan=copy.deepcopy(lis)
#集合按縱座標排序,找出y最小的點p0
lis_scan.sort(key=lambda x: x[1])
p0 = lis_scan[0]
#除去p0的其餘點集合
lis_scan.remove(p0)
#temp 存放要刪除的點
temp=[]
bubble_sort(lis_scan,p0,temp)
#print lis_scan
#print temp
#lis_scan_different存放刪除相同極角點後的集合
lis_scan_different=[]
for coordinate in lis_scan:
if coordinate not in temp:
lis_scan_different.append(coordinate)
#凸包為空
if len(lis_scan)==0:
print "null"
#p0,p1,p2壓入棧
Q.append(p0)
Q.append(lis_scan_different[0])
Q.append(lis_scan_different[1])
n=len(lis_scan_different)
for i in range(2,n):
control = True
while control:
if len(Q)<3:
break
#判斷topQ是否位於p0,pi,next_to_topQ三點構成的三角形內部
(t1, t2, t3) = isintriangle.isin(Q[-1], lis_scan_different[i], Q[-2], p0)
#topQ位於p0,pi,next_to_topQ三點構成的三角形內部,彈出topQ
if t1 >= 0 and t2 >= 0 and t3 >= 0:
Q.pop()
else:
control=False
#將pi加入棧
Q.append(lis_scan_different[i])
endtime = datetime.datetime.now()
print "grahamscan時間---",(endtime - starttime)
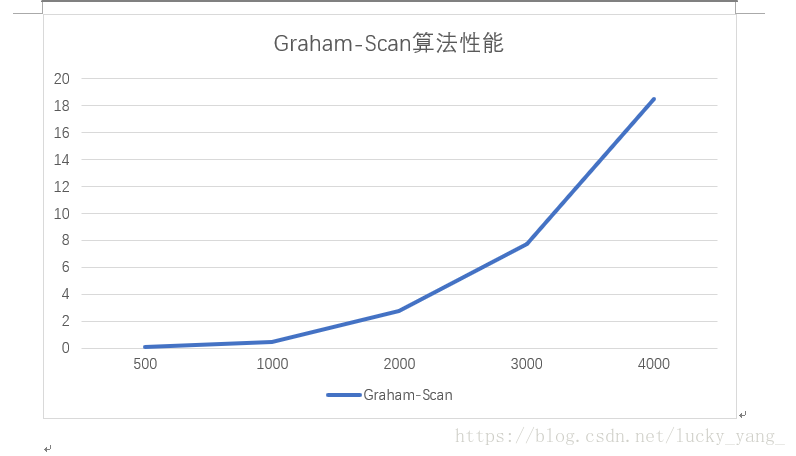
return QGraham-Scan演算法在點集數500、1000、2000、3000、4000的情況下得到演算法執行時間(秒),繪製成如下圖所示折線圖,可以看出在資料集較大的情況下,Graham-Scan演算法執行時間增長還在可以接受的範圍內, 效能也沒有降低很多。