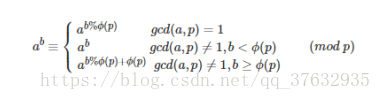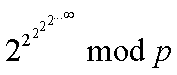一. 威爾遜定理

當p為素數時，（p-1）！= -1（mod p）

其逆定理也成立，移項得：（p-1）！+1整除p

二. 費馬小定理

當gcd（a，p）= 1且p為素數時，a ^（p-1）= 1（mod p）

而a ^ 0 = 1（mod p），因此存在長度為p-1的迴圈節，費馬鮮冪：a ^ b mod p = a ^（b mod p-1）mod p

三. 尤拉定理

當gcd（a，m）= 1時，

為小於m且與m互質數的個數，費馬小定理就是尤拉定理的一種特殊情況 

四. 裴蜀定理

對任意兩個整數a、b，設d是它們的最大公約數 

當且僅當 m 是 d 的倍數時，ax + by = m 才有整數解

擴充套件歐幾里得演算法即可求解

1）計算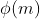值

① 先說明函式是積性函式，對於積性函式，若gcd（m，n）= 1，則 

②對於素數p，在1到p ^ k中p，2p，3p ......（p ^ k-1）p p p ^（k-1）個數與p ^ k不互質，因此

根據唯一分解定理，（pi為m的質因子），再根據上述兩點得到

2）計算1到m所有數的尤拉值（尤拉篩+積性函式）

void Get_Eular()
{
    int n = 0;
    phi[1] = 1;  
    for(int i=2;i<maxn;++i)
    {
        if(!phi[i])             //i為素數
        {
            phi[i] = i-1;       
            prime[n++] = i;
        }
        for(int j=0; j<n&&i*prime[j]<=maxn;++j)
        {
            if(i%prime[j]==0)
            {
                phi[i*prime[j]] = phi[i]*prime[j]; //i*prime[j]的素因子和i是一樣的,只相當與上文中的m擴大了
                break;
            }
            else phi[i*prime[j]] = phi[i]*phi[prime[j]];//積性函式的性質，i與prime[j]互質
        }
    }
}
 

3）尤拉因子求和

假設n的因子為d1，d2 ...... di，則尤拉函式和，F（n）也是積性函式，對於素數p，那麼p ^ k的因子就有p，p ^ 2，p ^ 3 ...... p ^ k，再結合公式②，得到，根據唯一分解定理,,有F（m）

4）互質數的和

在小於m的數中，與m互質的數的總和為： （n> 2），首先要知道若n與m互質，則mn與m互質，所以在m> 2時，與m互質的數總是一對一對的出現，且每一對的和為米，總共對

5）尤拉廣義降冪

不難發現：

當滿足gcd（A，P）= 1時， ，所以一個^ B

所以有：

注意判斷條件

四。尤拉廣義降冪應用

1. BZOJ 3884

描述：

解：

觀察上面的尤拉降冪就會發現這是一個遞迴，當披（）函式值為1時就遞迴結束，因為任何數對1取餘都等於0，而冪為無窮，恆滿足，所以：

程式碼：

#include<iostream>
using namespace std;
int Eular(int p)   //計算p的尤拉值
{
    int ans = p;
    for(int i=2;i*i<=p;++i)
    {
        if(p%i==0)
        {
            ans = ans - ans/i;
            while(p%i==0)
                p /= i;
        }
    }
    if(p>1) ans = ans - ans/p;
    return ans;
}
int quick_pow(int a,int x,int p)
{
    int ans = 1;
    while(x)
    {
        if(x&1) ans = ans*a%p;
        a = a*a%p;
        x>>=1;
    }
    return ans;
}
int cal(int p)
{
    int mod = Eular(p);
    if(mod==1) return quick_pow(2,0+1,p);
    return quick_pow(2,cal(mod)+mod,p);
}
int main()
{
    int p;
    while(cin>>p)
    {
        cout<<cal(p)<<endl;
    }
}

描述：

給定一個長度為Ñ的數列，每次查詢（L，R）

解：

和上面那題相比，此題不能直接得到冪和模的大小關係，我們依然可以一直遞迴下去，直到達r或phi（）值為1結束，但是冪和模的大小關係可以通過回溯回來的冪值和披（）來確定，

程式碼：

#include <algorithm>
#include <iostream>
#include <cstdio>
#include <map>
using namespace std;
typedef long long ll;
const int MAXN = 1e5+55;
int a[MAXN];
map <ll,ll> vis;          //記憶phi()，防止超時
ll Eular(ll n)
{
    if(vis[n]) return vis[n];
    ll ans = n;
    ll m = n;
    for(int i=2;i*i<=n;++i)
    {
        if(n%i==0)
        {
            ans = ans - ans/i;
            while(n%i==0)
                n = n/i;
        }
    }
    if(n>1) ans = ans - ans/n;
    return vis[m] = ans;
}
ll Quick_pow(ll a,ll x,ll mod)
{
    ll ans = 1;
    bool flag = false;   //標記冪(a^x)與mod的大小關係
    while(x)
    {
        if(x&1)
        {
            ans = ans*a;
            if(ans>=mod)
            {
                ans = ans%mod;
                flag = true;
            }
        }
        a = a*a;
        if(a>=mod && flag) 
        {
            a = a%mod;
        }
        x = x>>1;
    }
    return flag ? ans%mod+mod : ans;//廣義降冪的兩種情況
}
ll result(int l,int r,int m)
{
    if(l==r||m==1) return a[l]<m? a[l] : a[l]%m+m; 
    int phi = Eular(m);
    return Quick_pow(a[l],result(l+1,r,phi),m);
}
int main()
{
    int n,m,q,l,r;
    scanf("%d %d",&n,&m);
    for(int i=1;i<=n;++i)
        scanf("%d",&a[i]);
    scanf("%d",&q);
    while(q--)
    {
        scanf("%d %d",&l,&r);
        cout<<result(l,r,m)%m<<endl;
    }
    return 0;
}

看懂了上面的解法就會產生這樣一個疑問：在 ％p中，怎樣保證b ^ c與phi（p）的大小關係和b ^（回溯回來的冪）與phi（p）的大小關係一致？

證明：

回溯C時需要判斷C和   的關係，設回溯的冪為K.

1.如果，則K還是C;若b = 1，b ^ c = b ^ k，關係一致

證明b> 1時，：

如果b和p互質，由尤拉定理：，且b> 1，而phi（p）不會為0，則  ，

如果b和p不互質，令b'= b / gcd（b，p），b'和p互質，而b'<b，所以  ，得證

2.如果，則： ，即：，關係一致

五。經典例題

6.  牛客網 （裴蜀定理）

六。說明

個人認為證明過程沒必要過多糾結！