深度學習之---複雜性分析（引數量和計算次數）

阿新 • • 發佈：2018-12-18

卷積神經網路的複雜度分析

轉行修行中

在梳理CNN經典模型的過程中，我理解到其實經典模型演進中的很多創新點都與改善模型計算複雜度緊密相關，因此今天就讓我們對卷積神經網路的複雜度分析簡單總結一下下。

本文主要關注的是針對模型本身的複雜度分析（其實並不是很複雜啦～）。如果想要進一步評估模型在計算平臺上的理論計算效能，則需要了解 Roofline Model 的相關理論，歡迎閱讀本文的進階版： Roofline Model與深度學習模型的效能分析。

“複雜度分析”其實沒有那麼複雜啦~

1. 時間複雜度

即模型的運算次數，可用 $\textbf{FLOPs}$ 衡量，也就是浮點運算次數（FLoating-point OPerations）。

1.1 單個卷積層的時間複雜度

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\textbf{Time} \sim O(M^2 \cdot K^2 \cdot C_{in} \cdot C_{out})\quad\quad\quad\quad\quad\quad\quad\quad\quad$

$M$ 每個卷積核輸出特徵圖 $(Feature~\color{red}{M}ap)$ 的邊長
$K$ 每個卷積核 $(\color{red}{K}ernel)$ 的邊長
$C_{in}$ 每個卷積核的通道數，也即輸入通道數，也即上一層的輸出通道數。
$C_{out}$ 本卷積層具有的卷積核個數，也即輸出通道數。
可見，每個卷積層的時間複雜度由輸出特徵圖面積 $M^2$ 、卷積核面積 $K^2$ 、輸入 $C_{in}$ 和輸出通道數 $C_{out}$ 完全決定。
其中，輸出特徵圖尺寸本身又由輸入矩陣尺寸 $X$ 、卷積核尺寸 $K$ 、 $Padding$ 、 $Stride$ 這四個引數所決定，表示如下：

$\quad\quad\quad\quad\quad\quad\quad\quad M = (X - K + 2 * Padding) / Stride + 1 \quad\quad\quad\quad\quad\quad\quad\quad$

注1：為了簡化表示式中的變數個數，這裡統一假設輸入和卷積核的形狀都是正方形。
注2：嚴格來講每層應該還包含 1 個 $Bias$ 引數，這裡為了簡潔就省略了。

1.2 卷積神經網路整體的時間複雜度

$\quad\quad\quad\quad\quad\quad\quad\quad\quad \textbf{Time} \sim O\Bigg(\sum_{l=1}^{D} M_l^2 \cdot K_l^2 \cdot C_{l-1} \cdot C_{l}\Bigg) \quad\quad\quad\quad\quad\quad\quad\quad\quad$

$D$ 神經網路所具有的卷積層數，也即網路的深度。
$l$ 神經網路第 $l$ 個卷積層
$C_l$ 神經網路第 $l$ 個卷積層的輸出通道數 $C_{out}$ ，也即該層的卷積核個數。
對於第 $l$ 個卷積層而言，其輸入通道數 $C_{in}$ 就是第 $(l - 1)$ 個卷積層的輸出通道數。
可見，CNN整體的時間複雜度並不神祕，只是所有卷積層的時間複雜度累加而已。
簡而言之，層內連乘，層間累加。

示例：用 Numpy 手動簡單實現二維卷積

假設 Stride = 1, Padding = 0, img 和 kernel 都是 np.ndarray.

def conv2d(img, kernel):
    height, width, in_channels = img.shape
    kernel_height, kernel_width, in_channels, out_channels = kernel.shape
    out_height = height - kernel_height + 1
    out_width = width - kernel_width + 1
    feature_maps = np.zeros(shape=(out_height, out_width, out_channels))
    for oc in range(out_channels):              # Iterate out_channels (# of kernels)
        for h in range(out_height):             # Iterate out_height
            for w in range(out_width):          # Iterate out_width
                for ic in range(in_channels):   # Iterate in_channels
                    patch = img[h: h + kernel_height, w: w + kernel_width, ic]
                    feature_maps[h, w, oc] += np.sum(patch * kernel[:, :, ic, oc])

    return feature_maps

2. 空間複雜度

空間複雜度（訪存量），嚴格來講包括兩部分：總引數量 + 各層輸出特徵圖。

引數量：模型所有帶引數的層的權重引數總量（即模型體積，下式第一個求和表示式）
特徵圖：模型在實時執行過程中每層所計算出的輸出特徵圖大小（下式第二個求和表示式）

$\quad\quad\quad\quad\quad\quad\quad\quad\quad \textbf{Space} \sim O\Bigg(\sum_{l=1}^{D} K_l^2 \cdot C_{l-1} \cdot C_{l} + \sum_{l=1}^{D} M^2 \cdot C_l \Bigg) \quad\quad\quad\quad\quad\quad\quad\quad\quad$

總引數量只與卷積核的尺寸 $K$ 、通道數 $C$ 、層數 $D$ 相關，而與輸入資料的大小無關。
輸出特徵圖的空間佔用比較容易，就是其空間尺寸 $M^2$ 和通道數 $C$ 的連乘。
注：實際上有些層（例如 ReLU）其實是可以通過原位運算完成的，此時就不用統計輸出特徵圖這一項了。

3. 複雜度對模型的影響

時間複雜度決定了模型的訓練/預測時間。如果複雜度過高，則會導致模型訓練和預測耗費大量時間，既無法快速的驗證想法和改善模型，也無法做到快速的預測。
空間複雜度決定了模型的引數數量。由於維度詛咒的限制，模型的引數越多，訓練模型所需的資料量就越大，而現實生活中的資料集通常不會太大，這會導致模型的訓練更容易過擬合。
當我們需要裁剪模型時，由於卷積核的空間尺寸通常已經很小（3x3），而網路的深度又與模型的表徵能力緊密相關，不宜過多削減，因此模型裁剪通常最先下手的地方就是通道數。

4. Inception 系列模型是如何優化複雜度的

通過五個小例子說明模型的演進過程中是如何優化複雜度的。

4.1 $\textbf{InceptionV1}$ 中的 $1 \times 1$ 卷積降維同時優化時間複雜度和空間複雜度

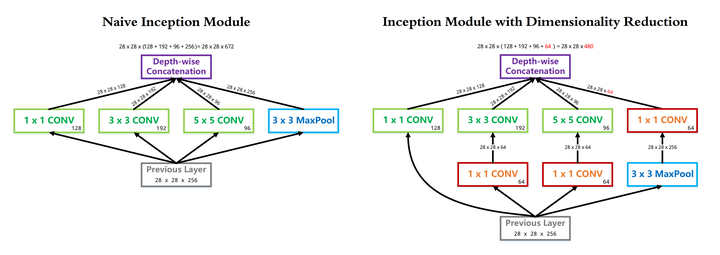
（影象被壓縮的慘不忍睹...）

InceptionV1 借鑑了 Network in Network 的思想，在一個 Inception Module 中構造了四個並行的不同尺寸的卷積/池化模組（上圖左），有效的提升了網路的寬度。但是這麼做也造成了網路的時間和空間複雜度的激增。對策就是新增 1 x 1 卷積（上圖右紅色模組）將輸入通道數先降到一個較低的值，再進行真正的卷積。
以 InceptionV1 論文中的 (3b) 模組為例（可以點選上圖看超級精美的大圖），輸入尺寸為 $28 \times 28 \times 256$ ， $1 \times 1$ 卷積核 $128$ 個， $3 \times 3$ 卷積核 $192$ 個， $5 \times 5$ 卷積核 $96$ 個，卷積核一律採用 Same Padding 確保輸出不改變尺寸。
在 $3 \times 3$ 卷積分支上加入 $64$ 個 $1 \times 1$ 卷積前後的時間複雜度對比如下式：

$\begin{aligned} \quad\quad\quad &\textbf{Before}\quad 28^2 \cdot 3^2 \cdot \color{blue}{256} \cdot \color{blue}{192} = 3.5 \times 10^8 \quad\quad\quad\\[2ex] \quad\quad\quad &\textbf{After} \quad~~ 28^2 \cdot 1^2 \cdot \color{blue}{256} \cdot \color{red}{64} + 28^2 \cdot 3^2 \cdot \color{red}{64} \cdot \color{blue}{192} = 1 \times 10^8 \quad\quad\quad \end{aligned}$

同理，在 $5 \times 5$ 卷積分支上加入 $64$ 個 $1 \times 1$ 卷積前後的時間複雜度對比如下式：

$\begin{aligned} \quad\quad\quad &\textbf{Before}\quad 28^2 \cdot 5^2 \cdot \color{blue}{256} \cdot \color{blue}{96} = 4.8 \times 10^8 \quad\quad\quad\\[2ex] \quad\quad\quad &\textbf{After} \quad~~ 28^2 \cdot 1^2 \cdot \color{blue}{256} \cdot \color{red}{64} + 28^2 \cdot 5^2 \cdot \color{red}{64} \cdot \color{blue}{96} = 1.3 \times 10^8 \quad\quad\quad \end{aligned}$

可見，使用 $1 \times 1$ 卷積降維可以降低時間複雜度3倍以上。該層完整的運算量可以在論文中查到，為 300 M，即 $3 \times 10^8$ 。
另一方面，我們同樣可以簡單分析一下這一層引數量在使用 1 x 1 卷積前後的變化。可以看到，由於 1 x 1 卷積的新增，3 x 3 和 5 x 5 卷積核的引數量得以降低 4 倍，因此本層的引數量從 1000 K 降低到 300 K 左右。

$\quad\quad\quad \textbf{Before} \begin{cases} 1^2 \cdot 256 \cdot 128 \\[1ex] 3^2 \cdot \color{red}{256} \cdot 192 \\[1ex] 5^2 \cdot \color{red}{256} \cdot 96 \end{cases} \quad\Longrightarrow\quad \textbf{After} \begin{cases} 1^2 \cdot 256 \cdot 128 \\[1ex] 1^2 \cdot 256 \cdot 64 \\[1ex] 3^2 \cdot \color{green}{64} \cdot 192 \\[1ex] 1^2 \cdot 256 \cdot 64 \\[1ex] 5^2 \cdot \color{green}{64} \cdot 96 \\[1ex] 1^2 \cdot 256 \cdot 64 \end{cases} \quad\quad\quad$

4.2 $\textbf{InceptionV1}$ 中使用 $GAP$ 代替 $Flatten$

全連線層可以視為一種特殊的卷積層，其卷積核尺寸 $K$ 與輸入矩陣尺寸 $X$ 一模一樣。每個卷積核的輸出特徵圖是一個標量點，即 $M = 1$ 。複雜度分析如下：

$\begin{aligned} &\quad\quad\quad\quad\quad\quad\quad\quad\quad\textbf{Time} \sim O(1^2 \cdot X^2 \cdot C_{in} \cdot C_{out})\quad\quad\quad\quad\quad\quad\quad\quad\quad\\[2ex] &\quad\quad\quad\quad\quad\quad\quad\quad\quad\textbf{Space} \sim O(X^2 \cdot C_{in} \cdot C_{out})\quad\quad\quad\quad\quad\quad\quad\quad\quad \end{aligned}$

可見，與真正的卷積層不同，全連線層的空間複雜度與輸入資料的尺寸密切相關。因此如果輸入影象尺寸越大，模型的體積也就會越大，這顯然是不可接受的。例如早期的VGG系列模型，其 90% 的引數都耗費在全連線層上。
InceptionV1 中使用的全域性平均池化 GAP 改善了這個問題。由於每個卷積核輸出的特徵圖在經過全域性平均池化後都會直接精煉成一個標量點，因此全連線層的複雜度不再與輸入影象尺寸有關，運算量和引數數量都得以大規模削減。複雜度分析如下：

$\begin{aligned} &\quad\quad\quad\quad\quad\quad\quad\quad\quad\textbf{Time} \sim O(C_{in} \cdot C_{out})\quad\quad\quad\quad\quad\quad\quad\quad\quad\\[2ex] &\quad\quad\quad\quad\quad\quad\quad\quad\quad\textbf{Space} \sim O(C_{in} \cdot C_{out})\quad\quad\quad\quad\quad\quad\quad\quad\quad \end{aligned}$

4.3 $\textbf{InceptionV2}$ 中使用兩個 $3 \times 3$ 卷積級聯替代 $5 \times 5$ 卷積分支

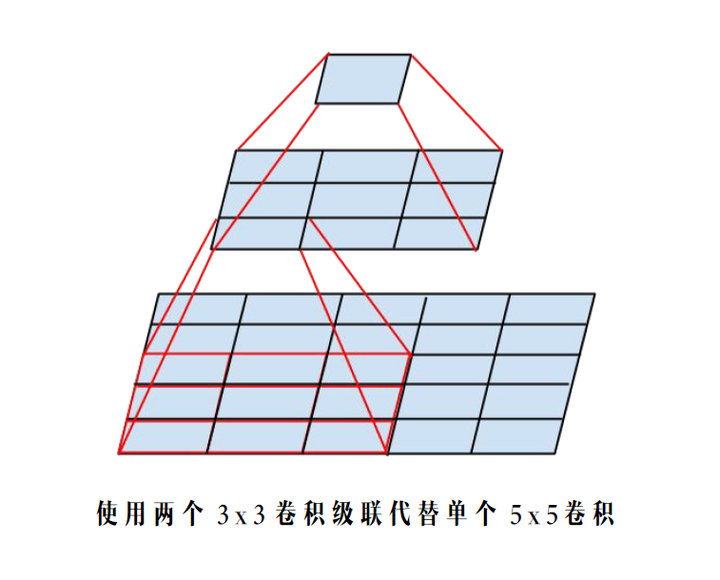
感受野不變

根據上面提到的二維卷積輸入輸出尺寸關係公式，可知：對於同一個輸入尺寸，單個 $5 \times 5$ 卷積的輸出與兩個 $3 \times 3$ 卷積級聯輸出的尺寸完全一樣，即感受野相同。
同樣根據上面提到的複雜度分析公式，可知：這種替換能夠非常有效的降低時間和空間複雜度。我們可以把辛辛苦苦省出來的這些複雜度用來提升模型的深度和寬度，使得我們的模型能夠在複雜度不變的前提下，具有更大的容量，爽爽的。
同樣以 InceptionV1 裡的 (3b) 模組為例，替換前後的 $5 \times 5$ 卷積分支複雜度如下：

$\begin{aligned} \quad\quad\quad &\textbf{Before}\quad 28^2 \cdot 1^2 \cdot 256 \cdot 64 + 28^2 \cdot \color{green}{5}^2 \cdot 64 \cdot 96 = 1.3 \times 10^8 \quad\quad\quad\\[2ex] \quad\quad\quad &\textbf{After} \quad~~ 28^2 \cdot 1^2 \cdot 256 \cdot 64 + 28^2 \cdot \color{green}{3}^2 \cdot 64 \cdot 96 \cdot \color{red}{2} = 1.0 \times 10^8 \quad\quad\quad \end{aligned}$

4.4 $\textbf{InceptionV3}$ 中使用 $N \times 1$ 與 $1 \times N$ 卷積級聯替代 $N \times N$ 卷積

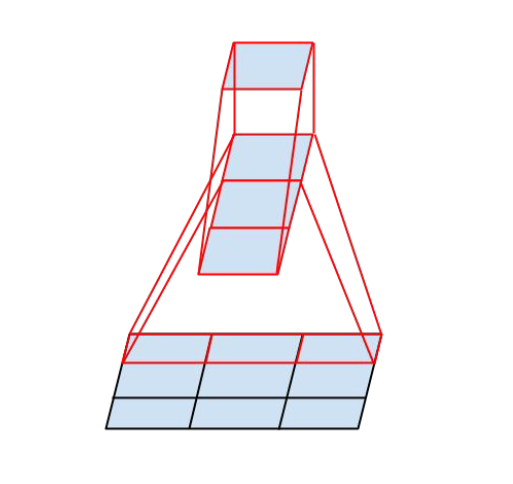
InceptionV3 中提出了卷積的 Factorization，在確保感受野不變的前提下進一步簡化。
複雜度的改善同理可得，不再贅述。

4.5 $\textbf{Xception}$ 中使用 $\textbf{Depth-wise Separable Convolution}$

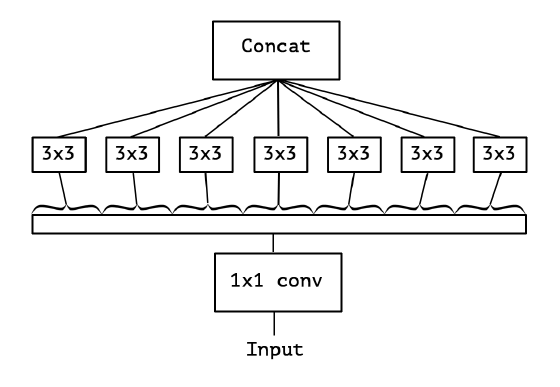
我們之前討論的都是標準卷積運算，每個卷積核都對輸入的所有通道進行卷積。
Xception 模型挑戰了這個思維定勢，它讓每個卷積核只負責輸入的某一個通道，這就是所謂的 Depth-wise Separable Convolution。
從輸入通道的視角看，標準卷積中每個輸入通道都會被所有卷積核蹂躪一遍，而 Xception 中每個輸入通道只會被對應的一個卷積核掃描，降低了模型的冗餘度。
標準卷積與可分離卷積的時間複雜度對比：可以看到本質上是把連乘轉化成為相加。

$\begin{aligned} \textbf{Standard Convolution} \quad {Time} &\sim O\Big(M^2 \cdot K^2 \cdot C_{in} \cdot C_{out}\Big)\\[3ex] \textbf{Depth-wise Separable Convolution} \quad {Time} &\sim O\Big(M^2 \cdot K^2 \cdot C_{in} + M^2 \cdot C_{in} \cdot C_{out}\Big) \end{aligned}$

5. 總結

通過上面的推導和經典模型的案例分析，我們可以清楚的看到其實很多創新點都是圍繞模型複雜度的優化展開的，其基本邏輯就是乘變加。模型的優化換來了更少的運算次數和更少的引數數量，一方面促使我們能夠構建更輕更快的模型（例如MobileNet），一方面促使我們能夠構建更深更寬的網路（例如Xception），提升模型的容量，打敗各種大怪獸，歐耶~

深度學習之---複雜性分析（引數量和計算次數）

卷積神經網路的複雜度分析

1. 時間複雜度

2. 空間複雜度

3. 複雜度對模型的影響

4. Inception 系列模型是如何優化複雜度的

5. 總結

深度學習之---複雜性分析（引數量和計算次數）

2018年11月13日Java學習之關鍵字static（類成員和類方法），單例設計，類的成員之：初始化塊

深度學習之神經網絡（CNN/RNN/GAN）算法原理+實戰

深度學習之PyTorch實戰（3）——實戰手寫數字識別

深度學習之神經網路（CNN/RNN/GAN）演算法原理+實戰目前最新

深度學習之物體檢測（一）R-CNN

深度學習之PyTorch實戰（1）——基礎學習及搭建環境

深度學習之PyTorch實戰（2）——神經網路模型搭建和引數優化

深度學習之神經網路（CNN/RNN/GAN） (演算法原理+實戰) 完整版下載

深度學習之啟用函式（Python實現）

深度學習之神經網路（CNN/RNN/GAN） (演算法原理+實戰)完整版

深度學習之數學基礎（概率與統計）

深度學習之：查全率（召回率recall）和查準率（精確率precision）

深度學習之路：（一）Keras中mnist資料集測試

深度學習之風格遷移（三）——Deep Photo Style Transfer(Fujun Luan)

深度學習之softmax函式（一）

深度學習網路篇——ZFNet（Part3 ZFNet的實驗環節）

深度學習網路篇——ZFNet（Part2 ZFNet的訓練細節）

深度學習網路篇——ZFNet（Part1 從AlexNet到ZFNet）

【ML1】機器學習之EM演算法（含演算法詳細推導過程）

深度學習之---複雜性分析（引數量和計算次數）

卷積神經網路的複雜度分析

1. 時間複雜度

2. 空間複雜度

3. 複雜度對模型的影響

4. Inception 系列模型是如何優化複雜度的

5. 總結

相關推薦