傳送門：https://leetcode-cn.com/problems/powx-n/

一、LeetCode 50. Pow(x, n)

1、題目描述

實現 pow(x, n) ，即計算 x 的 n 次冪函式。

2、示例

示例 1:

輸入: 2.00000, 10
輸出: 1024.00000

示例 2:

輸入: 2.10000, 3
輸出: 9.26100

示例 3:

輸入: 2.00000, -2
輸出: 0.25000
解釋: 2-2 = 1/2^2 = 1/4 = 0.25

3、說明

-100.0 < x < 100.0
n 是 32 位有符號整數，其數值範圍是 [−231, 231 − 1] 。

4、分析

本題重點在於邊界條件的分析和處理

• 如果 n < 0，是不是 n = -n， x = 1 / x ，再進行遞迴就能解決了呢？
• 如果 n = Intege.MIN_VALUE，n = -n 會出現溢位，怎麼辦呢？
• 我們可以先將 n / 2 賦值給 a，再將 a = -n，就不會出現溢位問題。

5、實現

class Solution {
public:
    double myPow(double x, int n) {
        if(n == 0)
            return 1;
        int a = n/2;
        if
 
(n < 0)
        {
            a = -a;
            x = 1.0/x;
        }    
        double res = myPow(x, a);
        if(n % 2 == 0)
            return res * res;
        else
            return res * res * x;
    }
};

二、遞迴

1、定義

• 若一個物件部分的包含自己或用它自己給自己定義，則這個物件是遞迴的；
• 若一個過程直接或間接的呼叫自己，則這個過程是遞迴的。

2、思想

把問題分解為規模更小具有與原問題相同解法的子問題
==》優點：思考的方式更加簡單，程式也更加簡練。
==》缺點：增加了壓棧開銷，因此空間複雜度比較高。

3、遞迴條件

• 減小問題規模，並使子問題與原問題有相同解法。
• 設定出口，如果沒有出口那麼程式會一直遞迴下去。

三、斐波那契數列

斐波那契數列是一個非常典型的遞迴問題。

1、迴圈方法

long Fibonacci1(size_t N)
{
	long first = 1;
	long second = 1;
	long sum = 0;
	if(N < 3)
		return 1;
	else
	{
		for(size_t i = 3; i <= N; i++)
		{
			sum = first + second;
			first = second;
			second = sum;
		}
		return sum;
	}
}

==》時間複雜度：O(n)
==》空間複雜度：O(1)

2、遞迴方法1

long Fibonacci2(size_t N)
{
	if(N < 3)
		return 1;
	else
		return Fibonacci2(N-1) + Fibonacci2(N-2);
}

==》由後向前計算
==》時間複雜度：O(n²)
==》空間複雜度：O(n)

3、遞迴方法2

long Fibonacci3(long first, long second, size_t N)
{
	if(N < 3)
		return second;
	else
		return Fibonacci3(second, first + second, N - 1);
}

==》前向後計算——尾遞迴方法
==》在進行遞迴時函式只會使用第一次壓棧所開闢的棧空間，在一個棧空間內迴圈，而不會開闢別的棧空間，所以這種方式時間複雜度為O(N)，空間複雜度為O(1)，是一種非常高效的遞迴方式。

4、遞迴方法3

long *Fibonacci4(size_t N)
{
	long *array = new long[N+1];
	if(N == 0)
		return NULL;
	array[0] = 1;
	array[1] = 1;
	for(size_t i = 2; i <= N; i++)
	{
		array[i] = array[i-1] + array[i-2];
	}
	return array;
}

四、遞迴函式的複雜度

在演算法的分析中，當一個演算法中包含遞迴呼叫時，其時間複雜度的分析==》一個遞迴方程的求解。

而對遞迴方程的求解，目前主流的方法：代入法，迭代法，公式法，母函式法，差分方程法。

1、代入法

• 首先要對這個問題的時間複雜度做出預測；
• 然後將預測帶入原來的遞迴方程，如果沒有出現矛盾，則是可能的解；
• 最後用數學歸納法證明。

示例
遞迴問題：T(n)=4T(n/2)+O(n)
（1）預測時間複雜度：O(n²)
（2）設T(n)=kn2（其中k為常數），將該結果帶入方程
（3）可得：左=kn2，右=4k(n/2)2+O(n)=kn2+O(n)
（4）由於n² 的階高於 n 的階，因而左右兩邊是相等的；
（5）數學歸納法進行驗證即可

2、迭代法

• 迭代的展開方程的右邊，直到沒有可以迭代的項為止；
• 這時通過對右邊的和進行估算來估計方程的解。
• 比較適用於分治問題的求解。

遞迴方程的一般形式

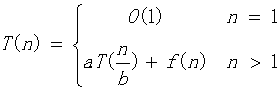
示例
（1）遞迴方程如下： $T(n) = 2T(n / 2) + n^2$

（2）迭代過程如下：
$T(n) = 2T(\frac{n}{2}) + n^2$ $= n^2 +2((\frac{n}{2})^2 + 2T(\frac{n}{4}))$ $= n^2 +2((\frac{n}{2})^2 + 2((\frac{n}{4})^2 + 2T(\frac{n}{8})))$ $= n^2 +2((\frac{n}{2})^2 + 2((\frac{n}{4})^2 +...+ 2((\frac{n}{2^i})^2 + 2T(\frac{n}{2^{i+1}}))))$

容易知道，直到 $\frac{n}{2^{i+1}}=1$ 時，遞迴過程結束，這時我們計算如下：
　 $T(n) = n^2 + 2 \frac{n^2}{2^2}+2^2\frac{n^2}{4^2}+2^2\frac{n^2}{8^2}+...$ $=n^2(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...)$ $=2n^2$
==》該演算法的時間複雜度：O(n²)

3、公式法

針對形如：T(n) = aT(n/b) + f(n)的遞迴方程
==》分治法的時間複雜度，即一個規模為n的問題被分成規模均為n/b的a個子問題，遞迴地求解這a個子問題，然後通過對這a個子問題的解的綜合，得到原問題的解。
==》公式法對於分治問題最好的解法

$ T ( n ) = { O ( n l o g b a ) , O ( n l o g b a ) &gt; O ( 相關推薦 【程式設計5】斐波那契數列 + 遞迴+LeetCode50 傳送門：https://leetcode-cn.com/problems/powx-n/ 一、LeetCode 50. Pow(x, n) 1、題目描述 實現 pow(x, n) ，即計算 x 的 n 次冪函式。 2、示例 示例 1: 輸入: 2.00000, 1 【劍指offer】斐波那契數列 遞迴 迴圈 時間 c++ 題目：大家都知道斐波那契數列，現在要求輸入一個整數n，請你輸出斐波那契數列的第n項（從0開始，第0項為0）。n<=39 思路：可以用兩種方法實現，這裡遞迴的辦法因為有太多重複的計算會超時（計算n=39，需要4s左右，題目要求1s），遂改用迴圈語句寫（經測試n=39時，完全小於1s），下面的程式碼中也給 【C語言】斐波那契數列的兩種演算法（迴圈，遞迴） #include<stdio.h> int Fabio(int n) //迴圈 { int i; int f1 = 1; int f2 = 1; int f3 = 1; for(i = 2;i<n;i++) { f3 = f1 + f Haskell 斐波那契 數列 遞迴實現 haskell let fibonacci n = if n < 3 then 1 else fibonacci (n-2) + fibonacci(n-1) Prelude> fi C++ 求斐波那契數列 遞迴法 迭代法 程式碼： /*遞迴法、迭代法求斐波那契數列*/ #include <iostream> #include <stdio.h> using namespace std; clas 斐波那契數列--遞迴與非遞迴實現 初識斐波那契數列： 斐波那契數列（Fibonacci sequence），又稱黃金分割數列、因數學家列昂納多·斐波那契（Leonardoda Fibonacci）以兔子繁殖為例子而引入，故又稱為“兔子 斐波那契數列 遞迴超時問題 斐波那契數列 在進行演算法運算時，使用遞迴運算，運算速度較慢。根據要求用陣列儲存比較快。 這次的題目中，是直接計算其餘數。 題目： Fibonacci數列的遞推公式為：Fn=Fn-1+Fn-2，其 斐波那契數列---遞迴和遞迴優化 斐波那契數列：        經典數學問題之一；斐波那契數列，又稱黃金分割數列，指的是這樣一個數列：   1、1、2、3、5、8、13、21、…… 想必看到這個數列大家很容易的就推算出來後面好幾項的值 斐波那契數列遞迴與非遞迴實現（JAVA語言描述） 斐波那契數列（Fibonacci sequence），又稱黃金分割數列、因數學家列昂納多·斐波那契（Leonardoda Fibonacci[1] ）以兔子繁殖為例子而引入，故又稱為“兔子數列”，指的是這樣一個數列：0、1、1、2、3、5、8、13、21、34 斐波那契數列遞迴與非遞迴 斐波那契數列的表示式： Fibonacci數列簡介： F(1)=1 F(2)=1 F(n)=F(n-1)+F(n-2) (n>2) 遞迴演算法程式： int f(int n) { if (n == 1 || n == 2) return 1; els 斐波那契數列遞迴演算法和非遞迴演算法以及其時間複雜度分析 1、在學習資料結構這門課的過程中，發現斐波那契數列的遞迴演算法以及非遞迴演算法，以及其時間複雜度分析是一個小難點。所以特別總結一下。 斐波那契數列的表示式： Fibonacci數列簡介： F(1)= 斐波那契數列(遞迴與非遞迴) 首先來說下遞迴，遞迴的思想是大事化小。斐波那契數列：1,1,2,3,5,8,13,21........設f(n)是第n個斐波那契數，當n<=2,斐波那契數都為1；當n>2,那麼第f(n)個斐波那契數就等於前兩個斐波那契數之和。遞迴的程式碼實現：#include&l 斐波那契數列——遞迴實現 #if 0 /*斐波那契數列： 題目：寫一個函式，輸入n，求斐波那契（Fibonacci)數列的第n項，斐波那契數列的定義如下： f(n) = 0 【洛谷P1962 斐波那契數列】矩陣快速冪+數學推導 公式 lin esp inline i++ out cin def res 來提供兩個正確的做法： 斐波那契數列雙倍項的做法（附加證明） 矩陣快速冪 一、雙倍項做法 在偶然之中，在百度中翻到了有關於斐波那契數列的詞條（傳送門），那麽我們可以發現一個這個規律$ \fra 【演算法 in python | DP】斐波那契數列vs卡塔蘭數列 1. 斐波那契數列 公式： 應用：爬樓梯 假設你正在爬樓梯。需要 n 階你才能到達樓頂。每次你可以爬 1 或 2 個臺階。你有多少種不同的方法可以爬到樓頂呢？ class Solution: def climbStairs(self, n): 【劍指offer】斐波那契數列非遞迴求解第N項 public class Solution {    public int Fibonacci(int n) {       //錯誤輸入處理       if 【劍指offer】斐波那契數列非遞歸求解第N項 非遞歸 acc 斐波那契 錯誤 bsp fibonacci 更新 off for public class Solution { public int Fibonacci(int n) { //錯誤輸入處理 if(n<0) return 【劍指offer第七題】斐波那契數列 題目描述 大家都知道斐波那契數列，現在要求輸入一個整數n，請你輸出斐波那契數列的第n項（從0開始，第0項為0）。 n<=39 剛開始覺得輸入為一個數，然後找到這個數在斐波那契數列中的位置 【劍指offer{7-10}】斐波那契數列、跳臺階、變態跳臺階、矩形覆蓋 斐波那契數列、跳臺階、變態跳臺階、矩形覆蓋題目描述C++程式碼跳臺階題目描述C++程式碼變態跳臺階題目描述C++程式碼矩形覆蓋題目描述C++程式碼 注：思路均是動態規劃，用中間陣列dp存放計算值，如果 【2018/10/08測試T1】【SOJ 2175】斐波那契 【題目】 題目描述： 斐波那契數列又稱兔子數列，可以通過以下方式產生：一開始只有一隻兔子，一個月之後這隻兔子每個月會繁殖出另一隻兔子。之後每隻兔子出生後都按照以上規則繁殖。我們把每個月的兔子的數量作為數列中的數就可以得到斐波那契數列。 現在草原上有 nnn 只兔 $