文章目錄

• 一、二叉樹的層次遍歷
• 1、題目描述——LeetCode.102
• 2、分析
• 3、實現
• 二、二叉樹(Binary Tree)
• 1、相關概念
• 二叉樹
• 滿二叉樹
• 完全二叉樹
• 區分
• 2、二叉樹的表示(儲存)
• （1）鏈式儲存法
• （2）順序儲存法
• （3）分析
• 3、二叉樹遍歷
• （1）方法
• （2）實現

一、二叉樹的層次遍歷

1、題目描述——LeetCode.102

給定一個二叉樹，返回其按層次遍歷的節點值。 （即逐層地，從左到右訪問所有節點）。

給定二叉樹: [3,9,20,null,null,15,7],

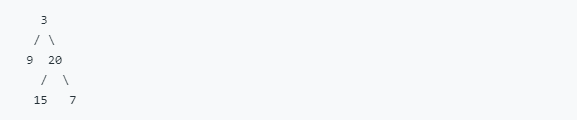
返回其層次遍歷結果：

2、分析

• 從輸出的結果來看，將根節點到葉子節點每層作為一個向量的二維向量中；
• 一般的遍歷：將節點儲存在佇列中，每次從隊首輸出一個節點並將其左右子節點插入到佇列中。
• 此題需要標記每層個數從而可以區分具體是哪層的節點==》nowcount、nextcount

3、實現

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        // 定義二維向量，儲存結果
 

        vector<vector<int>> res;
        if(root == NULL)
            return res;
        
        // 定義佇列 my_queue，儲存需要訪問的節點
        queue<TreeNode*> my_queue;
        my_queue.push(root);
        
        TreeNode *temp;
        
        vector<int> lev;
        lev.push_back(root->val);
        res.push_back(lev);
        
        // nowcount 用於標記本層還有幾個未遍歷的節點
        // nextcount 用於標記下一層的節點的個數
        int nowcount = 1, nextcount = 0;
        while(!my_queue.empty())
        {
            vector<int> lev;
            while(nowcount > 0){
                temp = my_queue.front();
                if(temp->left != NULL){
                    my_queue.push(temp->left);
                    nextcount++;
                    lev.push_back(temp->left->val);
                }
                if(temp->right != NULL){
                    my_queue.push(temp->right);
                    nextcount++;
                    lev.push_back(temp->right->val);
                }
                my_queue.pop();
                nowcount--;
            }
            if(!lev.empty())
                res.push_back(lev);
            nowcount = nextcount;
            nextcount = 0;
        }
        return res;
    }
};

二、二叉樹(Binary Tree)

1、相關概念

二叉樹

每個節點最多有兩個子節點（左子結點、右子節點）。

滿二叉樹

葉子節點全都在最底層，除葉子節點外，每個結點都有左右兩個子節點。

完全二叉樹

葉子節點都在最底下兩層，最後一層的葉子節點都靠左排列，並且除了最後一層，其他層的節點個數都要達到最大。

區分

2、二叉樹的表示(儲存)

兩種儲存方法：
①基於指標或引用的二叉鏈式儲存法——常用
②基於陣列的順序儲存方法。

（1）鏈式儲存法

每個節點有三個欄位，分別儲存：資料、指向左右子節點的指標。
==》只要通過根節點，就可以通過左右節點的指標，將整棵樹串起來。

（2）順序儲存法

一般情況下，為了方便計運算元節點，根節點會儲存在下標為 1 的位置。

• 將根節點儲存在下標 i = 1 的位置，其左節點儲存在下標 2 * i = 2 的位置，右子節點儲存在 2 * i + 1 = 3的位置。
• 依次類推：
  • 若結點 X 儲存在陣列中下標為 i 的位置，
  • 其左節點下標： 2 * i
  • 其右節點下標： 2 * i + 1
  • 其父節點下標：i / 2

（3）分析

若二叉樹為完全二叉樹，則陣列儲存是最節省記憶體的一種方式（不需要儲存額外的左右子節點的指標）

3、二叉樹遍歷

（1）方法

三種方法：前序遍歷、中序遍歷、後序遍歷
==》節點與它的左右子樹節點遍歷的先後順序：中代表該節點，左代表其左子樹，右代表其右子樹。

• 前序遍歷：中、左、右
• 中序遍歷：左、中、右
• 後序遍歷：左、右、中

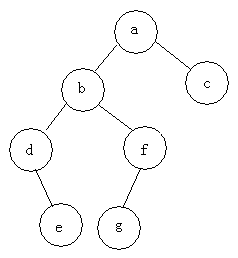
• 前序遍歷：abdefgc
• 中序遍歷：debgfac
• 後序遍歷：edgfbca

（2）實現

#include<iostream>
#include<string>
#include<stack>
#include<vector>
#include<queue>
using namespace std;

class BiNode{
public:
    char data;
    BiNode *lchild,*rchild;
};

// 對於二叉樹來說，只需要存放指向樹根節點的指標
class BiTree{
private:
    BiNode * root;
    int height;
    void pre_Order(BiNode *t);
    void in_Order(BiNode *t);
    void post_Order(BiNode *t);
    BiNode * create(string &s, int &ops);
    void get_Height(BiNode *t, int h);
public:
    BiTree()
    {
        root = NULL;
        height = 0;
    }
    // 按照前序遍歷序列建立二叉樹
    void createBiTree(string s);
    // 前序遍歷二叉樹
    void preOrder();
    // 中序遍歷二叉樹
    void inOrder();
    // 後序遍歷二叉樹（遞迴方法）
    void postOrder();
    // 後序遍歷二叉樹（使用棧的非遞迴方法）
    void postOrder1();
    // 層序遍歷二叉樹
    void levelOrder();
    // 二叉樹的高度
    int getHeight();
    // 求兩個節點的最大公共祖先
    void ancestor(char A, char B);
};

// 遞迴建立二叉樹，如果是#表示空節點
// 應用字串s建立二叉樹
BiNode * BiTree::create(string &s, int &pos)
{
    ++pos;
    BiNode *t;
    if((unsigned)pos >= s.size())
        return NULL;
    else{
        if(s[pos] == '#')
            t = NULL;
        else{
            t = new BiNode;
            t->data = s[pos];
            t->lchild = create(s, pos);
            t->rchild = create(s, pos);
        }
        return t;
    }
}

// 按照前序遍歷序列建立二叉樹
void BiTree::createBiTree(string s){
    int pos = -1;
    root = create(s, pos);
}

// 前序遍歷二叉樹
void BiTree::preOrder(){
    pre_Order(root);
    cout<<endl;
}
void BiTree::pre_Order(BiNode *t){
    if(t != NULL){
        cout<<t->data<<" ";
        pre_Order(t->lchild);
        pre_Order(t->rchild);
    }
}

// 中序遍歷二叉樹
void BiTree::inOrder(){
    in_Order(root);
    cout<<endl;
}
void BiTree::in_Order(BiNode *t){
    if(t != NULL)
    {
        in_Order(t->lchild);
        cout<<t->data<<" ";
        in_Order(t->rchild);
    }
}

// 後序遍歷二叉樹(遞迴方法)
void BiTree::postOrder()
{
    post_Order(root);
    cout<<endl;
}
void BiTree::post_Order(BiNode *t){
    if(t != NULL)
    {
        post_Order(t->lchild);
        post_Order(t->rchild);
        cout<<t->data<<" ";
    }
}

// 後序遍歷二叉樹(使用棧的非遞迴方法)
// 用r記錄右子樹是否遍歷，若沒有遍歷，則遍歷右子樹
void BiTree::postOrder1(){
    // p表示當前樹節點指標
    // r表示最近訪問的樹節點指標
    BiNode *p, *r;
    r = NULL;
    p = root;
    stack<BiNode*> my_stack;
    while(p!=NULL || !my_stack.empty())
    {
        if(p)
        {
            // 一直走到樹的最左邊
            my_stack.push(p);
            p = p->lchild;
        }
        else
        {
            p = my_stack.top();
            // 如果右子樹沒有遍歷，遍歷右子樹
            if(p->rchild != NULL && p->rchild != r)
            {
                p = p->rchild;
                my_stack.push(p);
                // 需要向左轉，否則將會遍歷右子樹節點兩邊
                p = p->lchild;
            }
            // 否則遍歷根節點
            else
            {
                p = my_stack.top();
                my_stack.pop();
                cout<<p->data<<" ";
                // 更新最近遍歷的節點
                r = p;
                // 將遍歷後的節點設為NULL，進行下一個節點的遍歷
                p = NULL;
            }
        }
    }
    cout<<endl;
}

// 使用佇列進行層序遍歷二叉樹
void BiTree::levelOrder()
{
    if(root == NULL)
        return;
    queue<BiNode*> my_queue;
    my_queue.push(root);
    while(!my_queue.empty()){
        BiNode *t;
        t = my_queue.front();
        my_queue.pop();
        cout<<t->data<<" ";
        if(t->lchild != NULL)
            my_queue.push(t->lchild);
        if(t->rchild != NULL)
            my_queue.push(t->rchild);
    }
    cout<<endl;
}

int BiTree::getHeight()
{
    get_Height(root,0);
    return height;
}
void BiTree::get_Height(BiNode *t, int h)
{
    if(t != NULL){
        ++h;
        if(h > height)
            height = h;
        get_Height(t->lchild, h);
        get_Height(t->rchild, h);
    }
}

int main(int argc, char const *argv[])
{
    BiTree a;
    string s;
    s = "ABD##E#F##C##";
    a.createBiTree(s);
    cout<<"前序遍歷: "<<endl;
    a.preOrder();
    cout<<"中序遍歷: "<<endl;
    a.inOrder();
    cout<<"後序遍歷1: "<<endl;
    a.postOrder();
    cout<<"後序遍歷2: "<<endl;
    a.postOrder1();
    cout<<"層序遍歷: "<<endl;
    a.levelOrder();
    cout<<"樹高:";
    cout<<a.getHeight()<<endl;
    return 0;
}