上一節我們詳細的介紹了嶺迴歸演算法和lasso演算法的來歷和使用，不過還沒有詳解lasso的計算方式，本節將進行全面的詳解，在詳解之前，希望大家都理解了嶺迴歸和lasso 的來歷，他們的區別以及使用的範圍。下面將開始詳解求解過程：

一樣的，講解之前先把本節需要的基礎知識和大家講講，這樣更容易理解：

本節需要大家理解方差、協方差以及相關係數，下面我們逐一來看一下，如果方差、協方差、相關係數的意義不理解的建議停下來好好學一學，不是隻看公式，要學習公式背後的意義，這才是重點，你只有懂了深層意義，你才知道如何使用它，切記。

方差：

根據上面定義，大家知道，E(x)是均值的意思，那麼X-E(x),就是衡量變數x偏離平均值的程度，但是呢X-E(x)可能為正可能為負，而且正負都可以代表偏離程度，關鍵是X-E(x)無法整體衡量變數x偏離中心的程度，因此就出現了

的平方項，為了求整體的偏離度，因此對求均值（資料與均值相減求和在求均值）即可: 這就是方差了，因為前面為了防止正負抵消加了平方項，這裡也要開方，開方後就是標準差了即資料平均偏離中心的程度了，因此方差是衡量資料（變數x）平均偏離中心的的程度的指標。

更深入詳細的理解建議看概率論相關的書籍，上面是一維變數x 的方差的定義，那如果是二維的呢？他們的方差如何定義？這些大家自己看看。

協方差：

在這裡預設大家都熟悉概率論了，我們知道在二維中，如果兩個隨機變數x,y相互獨立，那麼他麼的方差,那麼如果x，y不獨立呢？因此協方差的定義就出來了：

協方差的理解和方差差不多，區別在於，這裡的方差代表的是兩個變數共同決定偏離中心的程度，上面同時也給出了相關係數，就是協方差除以標準差，為什麼是需要除以各自的標準差呢？其實本質原因是消除兩個變數的幅值帶來的差異，因為相關係數是衡量兩個變數的變化趨勢的，和本身變化的多少沒關係，而本身的變化多少其實就是各自的方差了，大家仔細琢磨一下就明白了。

換個角度進行解：

相關係數也可以看成協方差：一種剔除了兩個變數量綱影響、標準化後的特殊協方差。

既然是一種特殊的協方差，那它：

1、也可以反映兩個變數變化時是同向還是反向，如果同向變化就為正，反向變化就為負。

2、由於它是標準化後的協方差，因此更重要的特性來了：它消除了兩個變數變化幅度的影響，而只是單純反應兩個變數每單位變化時的相似程度。

總結一下相關係數：衡量多個變數之間變化趨勢的量，和各自的變化多少沒關係，只和變化趨勢相關，因此：

當他們的相關係數為1時，說明兩個變數變化時的正向相似度最大，即，你變大一倍，我也變大一倍；你變小一倍，我也變小一倍。也即是完全正相關（以X、Y為橫縱座標軸，可以畫出一條斜率為正數的直線，所以X、Y是線性關係的）。

隨著他們相關係數減小，兩個變數變化時的相似度也變小，當相關係數為0時，兩個變數的變化過程沒有任何相似度，也即兩個變數無關。

當相關係數繼續變小，小於0時，兩個變數開始出現反向的相似度，隨著相關係數繼續變小，反向相似度會逐漸變大。

當相關係數為－1時，說明兩個變數變化的反向相似度最大，即，你變大一倍，我變小一倍；你變小一倍，我變大一倍。也即是完全負相關（以X、Y為橫縱座標軸，可以畫出一條斜率為負數的直線，所以X、Y也是線性關係的）。

我們知道了什麼是協方差，以及協方差的定義，那麼如果有一集合的樣本x，y，我們去中心化，標準化後，此時的均值為0，方差為1，那麼相關係數的定義就可以寫成：

                                         

這是根據上面的定義寫的，對E(xy)=xy這一步是因為上面進行了去中心化和標準化,後面會發現相關係數就是XY的內積，而內積的物理意義大家都知道了把，我在這篇文章詳細講解了設麼是內積，這點很重要，我們發現兩個變數的相關性和變數的內積有一定的關係，那麼相關性越大，內積的絕對值就越大，當內積為0時說明兩個變數不相關，同時說明兩個向量是垂直的，如果高度相關，說明兩個向量是共線的，大家需要理解，好到這裡基礎就講完了，下面我們開始今天的主角LAR解決lasso：

首先需要說明的是LAR(最小角迴歸)和lasso是兩個不同的演算法，但是二者在某些方面具有驚人的相識，然而lasso 的計算相當複雜，但是LAR的計算是很簡單的（這裡又體現了，很複雜的數學計算一般可以通過很簡單的數學計算得出，只是這個簡單的數學計算沒那麼容易想到而已），有多簡單呢？我們下面會詳說，因此人們就使用LAR近似的對lasso求解，雖然說是近似，但是和真實沒什麼區別了，下面先從LAR進行詳解：

LAR（最小角迴歸）

LAR(Least Angel Regression),Efron於2004年提出的一種變數選擇的方法，類似於向前逐步迴歸(ForwardStepwise)的形式，是lasso regression的一種高效解法。向前逐步迴歸(Forward Stepwise)不同點在於，Forward Stepwise每次都是根據選擇的變數子集，完全擬合出線性模型，計算出RSS，再設計統計量（如AIC）對較高的模型複雜度作出懲罰，而LAR是每次先找出和因變數相關度最高的那個變數, 再沿著LSE的方向一點點調整這個predictor的係數，在這個過程中，這個變數和殘差的相關係數會逐漸減小，等到這個相關性沒那麼顯著的時候，就要選進新的相關性最高的變數，然後重新沿著LSE的方向進行變動。而到最後，所有變數都被選中，就和LSE相同了。

下面我們詳解一下，先講解一下一點基礎知識：

這個圖大家不陌生生吧，在上一篇裡我詳細的講過，不知道的請看我的這篇文章，我們知道y是真實值，而就是擬合值了，而的就是在x1和x2確定的平面內，找到一點是的yy^最小的迴歸係數，此時就是最優解了，因為此時的誤差最小，那麼我們聯絡下上面的基礎可知，如果兩個向量相關性為0則說明兩個向量是正交的（垂直），我們還知道，距離最短時，一定是同時垂直x1和x2，這個不用解釋了吧，那麼如果推向多個變數的情況下也應該是這樣既應該垂直所有的時才是最優的，這裡大家一定要深入理解了，好，到這裡所有基礎都準備好了，下面正式引入LAR演算法：

什麼是最小角迴歸？最小角體現在哪裡？：

在這裡首先以二維講解，然後推向高維 ，如圖，二維x1和x2張成了一張平面（看不懂的看這篇文章），那麼就是在這個平面內找到最優值，其實就是找到垂直這個平面的，這個很好理解但是計算起來並不容易，現在有一種可行的方法，即我先計算所有的和的相關係數，然後排好序，找到相關係數最大的那個x，假如上圖就是x1和y的相關性最大，那麼我們要找的這一點先從x1和y交點處開始，此時先關性是最大的，那麼我沿著x1的方向移動那一點，上圖的黃線，此時相關性的計算相當於那個黃線的向量和x1的相關性，相關性從最大逐漸減小，在減小的過程中，在某一點，一定會和第二個向量的相關性相等，上圖以x2為第二個相關性，某一點就是黃線和虛線的交點，在這一點時，yx1的相關性和yx2的相關性是相等的（虛線就是x2，和先平行），此時我做條x1和x2的角平分線，然後黃線沿著角平分線繼續遊走，如下圖；

此時大家知道，因為沿著角平分線走，會發現黃線和x1和x2的相關性會同樣的變化，因為是內積，所以相等（平面中角平分線上的點到兩邊的距離相等） ，好此時我們加入的x2的相關性也一起減小了，同理減小到第三個量即x3和y的相關性相等，此時把第三個變數也加入，就這樣不停的遊走，直到加入所有的x，最後使相關性係數遊走到零這一點，而這一點就是最優點，相關係數為零說明，內積為零，內積為零說明相互垂直，因此此時的點對所有的x都是垂直的，這也點也就是我們一直說的最優點，因此就找到了，最小角就體現在角平分線的角，因為每次改變的方向就改變角，如果是高維的情況，則說明每次改變的會更小，因此是最小角迴歸，這個大家需要好好理解。

好，我們總結一下最小角迴歸：

首先計算所有的相關性，排序，剛開始最大的加入點就是y本身，相關性為1，然後選擇最大的相關性為第一個加入點，然後遊走，不停的計算相關係數，當減小到等於第二個相關係數時，把第二個變數加入，然後按照這兩個角平分線繼續遊走，以此類推加入第三個，第四個，直到全部加入，然後遊走到相關係數為0,這一點就是最優點了，以上就是最小角迴歸了，幾何意義很清晰，能想到這樣的解決方法都是牛叉之人，佩服。下面給出虛擬碼：

   1. 對資料進行去中心化和標準化，計算殘差：

   2.計算所有的和的相關係數，並選出最大的那個相關係數

   3. 最小二乘係數從0開始移動，並時刻計算 （相關係數）,直到和最大的相關係數相等，此時加入進來

   4.然後沿著共同決定的方向繼續前進，直到和下一個x相關係數相等，然後加入

    5.按照第3,4兩步。直到完全加入所有的變數x，

    6.加入完以後繼續遊走使其相關係數為零，此時的值就是最優值。

下面我們看看圖：

其中L1是每次加入變數後改變的弧長的累加和 詳解如下：

好我們來看看上圖，上圖橫軸為弧長，縱軸是相關係數，我們發現v2出的相關係數最大即水藍色，即先沿著v2減小，直到在v6時和藍線相等，然後根據角平分線繼續遊走減小，在v4時由加入一個，以此類推 一直加完所有的變數，然後是最後的相關係數走到0的點，此時就是最優點，從圖中我們還可以發現隨著不停的遊走，變數的相關係數在不停的變化，這個大家應該都能理解吧，所以每遊走一步都需要計算相關係數，而計算相關係數很簡單就是內積就可以了，以上就是最小角迴歸的工作原理，下面我們看看他和lasso有什麼關係：

大家看看，他們是不是很相似，只是某些細節不一樣，如果我們在矯正一下是不是就是一樣的呀，先給出矯正方式：

如果非零係數達到零，將其變數從活動變數集合中刪除，並重新計算當前最小二乘方向。

為什麼這兩個演算法如此相似呢？怎麼回事呢？下面我們來看到底為什麼他們那麼像。

先說明就是那本書對這解釋也是不清楚的，看的暈暈的，不過LAR容易解釋，但是lasso的那個過0時產生跳躍沒有講清楚，在這裡我根據我自己的理解說一下，如果哪位大神看到這裡，看出眉目了，知道到底是什麼原因一定要和我說呀，我也是太想知道了，好，下面開始：

LAR:

      對於最小角迴歸我們知道，他是根據誤差向量和新增的xi進行內積的，一旦內積完成在遊走時，符號（正負號）一般不會變，只會改變內積的大小，因此遊走表示式可以寫成下式：

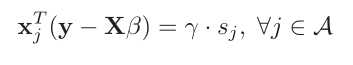
 A就是加入遊走的特徵向量集了，就是就是符號函式（大於0等於1，小於零等於-1），而就是內積的絕對值了，他有一個條件：

這個大家應該可以理解，就是沒加入遊走的特徵的內積一定小於 ，因為內積就是相關係數啊，遊走的順序是先從大的相關係數開始，逐漸減小到0的，因此還沒加入的特徵肯定小於的，這個大家可以理解對吧，那麼加入符號函式的目的是因為特徵向量可能是相反的即相關係數可能為負的，這個也容易理解，根據這個圖來看，沒有什麼特殊的點不滿足條件，因此是連續的，那麼我看看lasso ：

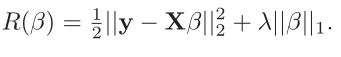
這個是我們最初優化的那個式子即誤差平方和，只是假如了一階的懲罰函式也就是lasso了 。通過這個式子我們需要解出，那就需要求導，因為加了絕對值，因此需要分情況討論，需要找到滿足所有駐點的關係式，於是經過大量的數學推倒找到了這個滿足所有駐點的方程式：

我們發現和lar很像，不同的是符號函式的情況，這也是導致差異的原因 ，我們知道得到這個式子的前提是對上式的求導，但是大家想想，這裡都滿足可導嗎？請看下圖：

我們發現除了約束條件的四個頂點不可導以外，其他均可導，不可導的情況就是某一個 為0，這也是是解釋了為什麼產生跳躍的原因，當然這是我的理解，仔細想想還是有點不對，但是那本書講的更簡略，他說是因為不滿足下面這個條件:

為了大神能看到，我把原文貼上來：

其中3.23時就是我們最初的迴歸表示式：

有搞明白的請留言，謝謝，或者加我微信zsffuture。

本篇就到此結束，基本上線性迴歸的理論就結束了，後面就是根據機器學習實戰進行實現了，後面的就不難了，如果理解到這裡你的思路還是很清晰說明你已經徹底的理解了，好，本節結束