上次我們留了個兩個問題沒有仔細說明，一個是區域性加權線性迴歸，另一個是嶺迴歸。今天依次對這兩種演算法進行說明。

一、區域性加權線性迴歸

　　欠擬合這種問題是僅僅憑藉一條直線來對資料點進行擬合的線性迴歸演算法所無法避免的，而解決這種欠擬合問題的方法中，有一種最為簡便，稱之為區域性加權線性迴歸。顧名思義，區域性加權線性迴歸就是指給被預測點周圍的資料點賦以不同的權重，讓預測更加註重區域性上的趨勢而不是整體上的趨勢，這樣的操作一旦不注意就會造成過擬合，所以應用的時候要特別注意。
　　該演算法對應的迴歸係數矩陣計算方法如下：
　　
　　　　　　　　　　　　　　　　θ=(XTWX)−

　　其中W為權重矩陣，它是一個m∗m的對角矩陣，訓練集中的樣本xi所對應的權重儲存在W(i,i)中。 為n∗m的矩陣， XTW仍舊為n∗m的矩陣，不同之處在於每個樣本都被賦予了不同的權重。
　　權重的計算方式有很多種，其主要目標就是賦予待遇測點周圍的資料點相對更高的權重，一般採用高斯核函式來實現這個目標，高斯核函式的形式如下：
　　
　　　　　　　　　　　　　　　　W(i,i)=exp(|xi−x|−2k2)

　
　　
　　我們可以注意到，k的取值越小，權重衰減的越快，僅僅在要預測的點附近很有限的資料點才可以對迴歸係數的學習起到作用，其他的資料點權重為0無法參與到迴歸係數的學習過程當中。
　　
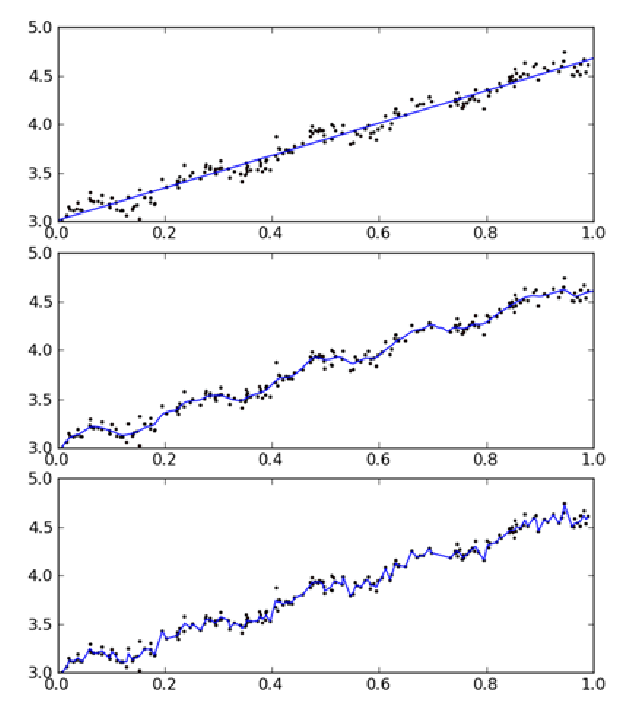
　　這種方法有助於避免簡單線性迴歸所帶來的欠擬合的問題，然而它可能會帶來過擬合的問題，如下圖所示：
　　　　　　　　

二、嶺迴歸

　　使用線性迴歸的一個前提是矩陣XTX為滿秩，這是因為若XTX 奇異則無法求逆，式θ=(XTX)−1XTy 無解。那麼什麼情況下矩陣XTX會出現無法求逆或者很難求逆的情況呢？當所有變數之間有較強的線性相關性時，或者變數之間的資料變化比較小或者部分變數之間有線性相關性時，矩陣X

TX的行列式比較小，甚至趨近於0，這時矩陣XTX很難求逆，簡單的線性迴歸方法無法適應這種情況。
　　在這種情況下，我們引入嶺迴歸，迴歸係數的計算公式變為：
　　　　　　　　　　　　　　　θ=(XTX+λI)−1XTy
　　嶺迴歸演算法通過引入λI來使得矩陣非奇異，可以求逆。嶺迴歸中的“嶺”就是指單位陣I的對角線像一條山嶺一樣。不過這種表達還是不夠直觀，我們從原始的目標函式來看，嶺迴歸的目標函式如下所示：
　　minw∑i=0n(yi−xTiθ)2+λ||θ||2
　　可以看到，嶺迴歸是在簡單線性迴歸的目標函式後面加了一個二範數懲罰項，其目的在於限制迴歸係數矩陣的取值，減少不必要的引數。顯然，對於不同的λ，迴歸係數向量θ會有不同的取值，反映θ隨λ變化的影象稱為嶺跡圖，如下所示：

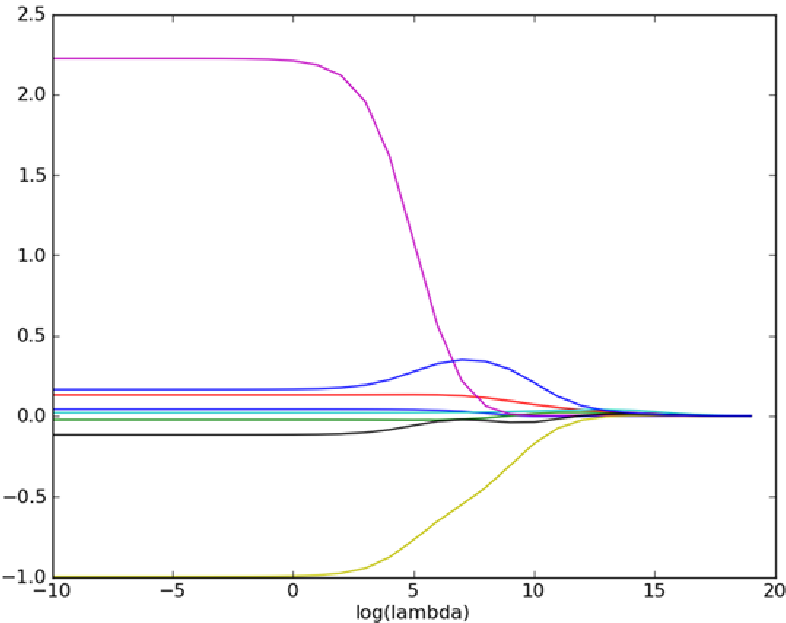
　　可以看到當λ取值很小時，迴歸係數矩陣並沒有什麼變化，隨著λ取值的逐漸增大，迴歸係數矩陣逐漸歸於0。另外我們還可以根據嶺跡圖看出哪一個特徵對最後的預測貢獻最大（資料要歸一化）。比如在上圖中最上面的一條線，迴歸係數最大，對最後預測的貢獻也就是最大。
簡而言之，嶺迴歸用於處理自變數之間高度相關的情形。線性迴歸的計算用的是最小二乘估計法，當自變數之間高度相關時，最小二乘迴歸估計的引數估計值會不穩定，這時如果在公式里加點東西，讓它變得穩定，那就解決了這一問題了。嶺迴歸就是這個思想。