AdaBoost 演算法-分析波士頓房價資料集
阿新 • • 發佈:2020-12-17
> **公號:碼農充電站pro**
> **主頁:**
在機器學習演算法中,有一種演算法叫做**整合演算法**,**AdaBoost 演算法**是整合演算法的一種。我們先來看下什麼是整合演算法。
### 1,整合演算法
通常,一個 **Boss** 在做一項決定之前,會聽取多個 **Leader** 的意見。**整合演算法**就是這個意思,它的基本含義就是**集眾演算法之所長**。
前面已經介紹過許多演算法,每種演算法都有**優缺點**。那麼是否可以將這些演算法**組合**起來,共同做一項決定呢?答案是肯定的。這就誕生了**整合演算法**(*Ensemble Methods*)。
整合演算法的基本架構如下:
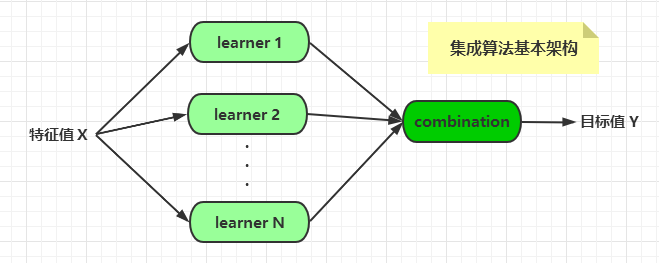
演算法的組合有多種形式,比如將不同的演算法整合起來,或者將同一種演算法以不同的形式整合起來。
常見的整合演算法有四大類:
- **bagging**:裝袋法,代表演算法為 [RandomForest](https://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm)(隨機森林)。
- **boosting**:提升法,代表演算法有 **AdaBoost**,**XGBoost** 等。
- **stacking**:堆疊法。
- **blending**:混合法。
多個演算法以不同的方式可以組合成**整合演算法**,如果再深入探究的話,不同的整合方法也可以組合起來:
- 如果將 **boosting** 演算法的輸出作為**bagging** 演算法的基學習器,得到的是 **MultiBoosting** 演算法;
- 如果將 **bagging** 演算法的輸出作為**boosting** 演算法的基學習器,得到的是 **IterativBagging** 演算法。
對於**整合演算法**的整合,這裡不再過多介紹。
### 2,bagging 與 boosting 演算法
**bagging**和 **boosting**是兩個比較著名的整合演算法。
***bagging 演算法***
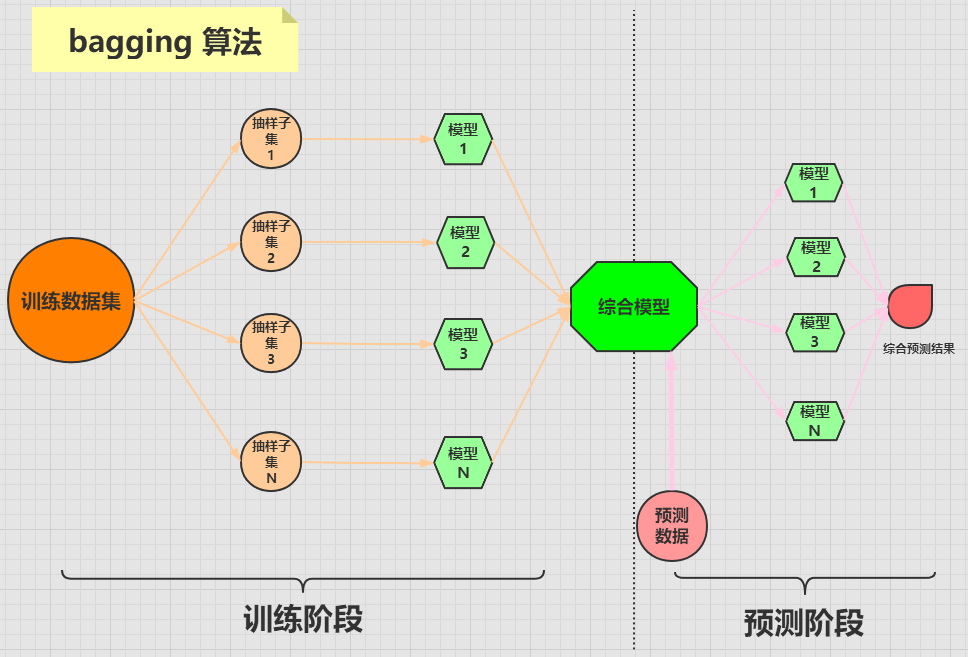
**bagging** 演算法是將一個原始資料集隨機抽樣成 **N** 個新的資料集。然後將這**N** 個新的資料集作用於**同一個**機器學習演算法,從而得到 **N** 個模型,最終整合一個**綜合模型**。
在對新的資料進行預測時,需要經過這 **N** 個模型(每個模型互不依賴干擾)的預測(投票),最終綜合 **N** 個投票結果,來形成最後的預測結果。
***boosting 演算法***
**boosting 演算法**的含義為**提升學習**,它將多個**弱分類器**組合起來形成一個**強分類器**。
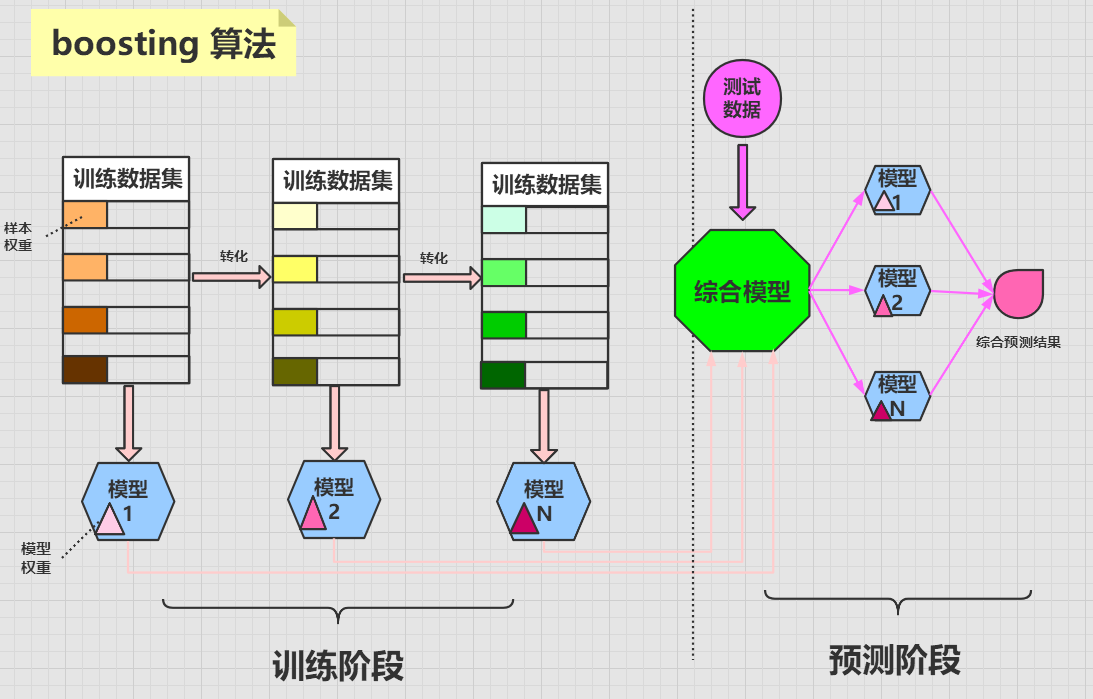
**boosting 演算法**是將一個原始資料集使用同一個演算法迭代學習 N 次,每次迭代會給資料集中的樣本分配不同的權重。
分類正確的樣本會在下一次迭代中降低權重,而分類錯誤的樣本會在下一次迭代中提高權重,這樣做的目的是,使得演算法能夠對其**不擅長(分類錯誤)的資料**不斷的**加強提升**學習,最終使得演算法的成功率越來越高。
每次迭代都會訓練出一個新的**帶有權重的模型**,迭代到一定的次數或者最終模型的錯誤率足夠低時,迭代停止。最終整合一個強大的**綜合模型**。
在對新的資料進行預測時,需要經過這 **N** 個模型的預測,每個模型的預測結果會帶有一個權重值,最終綜合 **N** 個模型結果,來形成最後的預測結果。
**boosting 演算法**中每個模型的權重是不相等的,而**bagging 演算法**中每個模型的權重是相等的。
### 3,AdaBoost 演算法
**AdaBoost 演算法**是非常流行的一種 **boosting** 演算法,它的全稱為 **Adaptive Boosting**,即**自適應提升學習**。
**AdaBoost 演算法**由**Freund** 和 **Schapire** 於**1995** 年提出。這兩位作者寫了一篇關於[AdaBoost 的簡介論文](http://cseweb.ucsd.edu/~yfreund/papers/IntroToBoosting.pdf),這應該是關於**AdaBoost** 演算法的最權威的資料了。為了防止連結丟失,我將論文下載了,放在了[這裡](https://codeshellme.github.io/books/IntroToBoosting.pdf)。
>
