--------韋訪 20181030

1、概述

這一講，我們來看看決策樹。

2、概念

決策樹（decision tree）是一種常用的分類與迴歸方法，其模型為樹狀結構，如下圖所示，

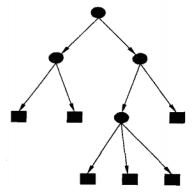
其中，最頂部的圓點為根節點，其他圓點為內部節點，方形為葉子節點。

決策樹一般分為三步：特徵選擇、生成決策樹、修剪決策樹。下面分別說明。

3、特徵選擇

特徵選擇的主要目的是選擇對訓練資料集具有最大的分類能力的特徵，以提高決策樹的學習效率，降低複雜度。

熵（entropy）：

怎麼判斷特徵選擇的分類能力呢？總得有個衡量標準吧？這個標準就是---熵

熵是表示隨機變數不確定性的度量。公式為：

圖形如下圖所示，

 由上圖可知，當P=0或者P=1時，H(X)=0，熵值為0，即事件為確定事件。 當P=0.5時，H(X)=1，熵值為1，此時隨機變數的不確定性最大。 舉個簡單的例子，有下面兩個集合， A集合：[1, 1, 1, 1, 1, 1, 1, 1, 2, 2] B集合：[1, 2, 3, 4, 5, 6, 7, 8, 9, 0] A集合比B集合相對穩定，所以熵也比B集合低。不確定性越大，熵值也就越大。 資訊增益（information gain）： 資訊增益表示特徵X使得類Y的不確定性減少的程度，資訊增益越大的特徵，表示其具有更強的分類能力。公式為，

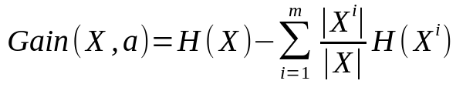
下面會舉個例子說明這個式子怎麼用的。

4、生成決策樹

為了方便講解，舉個例子說明，給出如下圖所示的14天的打球的資料，4種環境變化（outlook、temperature、humidity、windy）作為特徵，生成決策樹。

 按上面的資料，我們列出四種可能的劃分方式，如下圖所示，

那麼，應該選誰當根節點呢？上面說到，誰的資訊增益越大，誰的分類能力就越強，就該選誰作為節點。那麼，現在就分別計算它們的資訊增益。

14天中，有9天打球，5天不打球，那麼，熵為，

對於Outlook特徵:

Outlook=sunny時，熵值為，

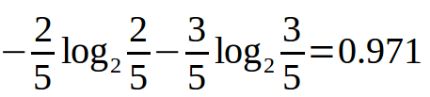
Outlook=overcast時，全都是yes，則熵值為0.

Outlook=rainy時，熵值為，

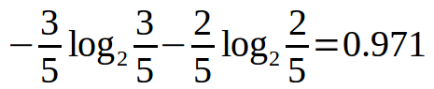
上面的根據資料表可得，Outlook分別為sunny、overcast、rainy的概率為5/14、4/14、5/14。則熵值為,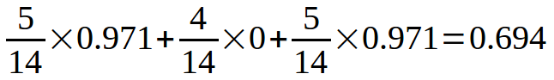 

 則Outlook的資訊增益為，

對於Temperature特徵:

Temperature=hot時，熵值為，

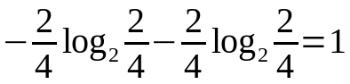
Temperature=mild時，熵值為， 

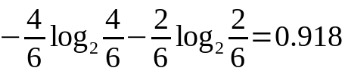
Temperature=cool時，熵值為， 

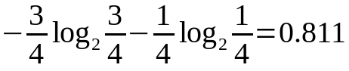
上面的根據資料表可得，Temperature分別為hot、mild、cool的概率為4/14、6/14、4/14。則熵值為,

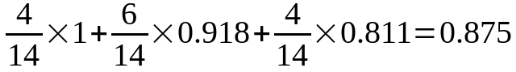
則Outlook的資訊增益為，

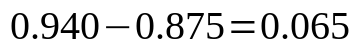
溼度和風就不算了，以此類推即可。

上面的演算法成為ID3演算法，ID3演算法根據信增益評估和選擇特徵。

但ID3演算法有個缺陷，比如，在上面的資料中，新增一個ID屬性，每一行的ID資料分別為1到14，那這個ID的熵為0，資訊增益是最大的，但是顯然這個ID對我們最終的結果是沒有任何影響的，所以就有了根據資訊增益率來選擇特徵的C4.5演算法。

資訊增益率的公式如下：

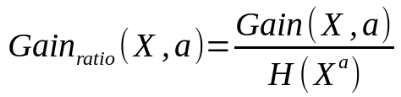
說白了，資訊增益率就是資訊增益除以自身熵。

CART決策樹：

CART決策樹使用基尼指數（Gini index）來選擇劃分屬性。公式如下，

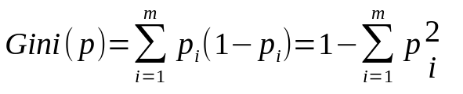
Gini係數用來衡量資料集的純度，反應了從資料集中隨機抽取兩個樣本，其標記列別不一致的概率，Gini係數越小，則資料集純度越高。它和熵的衡量標準類似，只是計算方式不同而已。

5、剪枝（prunning）

剪枝是為了防止決策樹演算法過擬合的主要手段，通過去掉一些分支來降低過擬合的風險。

剪枝是指將一顆子樹的子節點去掉，根節點作為葉子節點，如下圖，

剪枝策略一般分兩種：預剪枝、後剪枝。

預剪枝是邊建立決策樹邊進行剪枝操作。後剪枝是建立完決策樹後，再進行剪枝操作。

預剪枝有欠擬合的風險，後剪枝可以得到泛化能力更強的決策樹，但開銷會更大。

預剪枝演算法：

預剪枝策略一般為：限制深度、葉子節點個數、葉子節點樣本數、資訊增益量等。

限制深度比較好理解，如下圖所示，如果限制深度為3，那麼，第3層以下的節點都去除即可。

限制葉子節點個數如下圖，如果要葉子節點為3，則當葉子節點為3時，就不繼續建立節點了。

後剪枝演算法：

後剪枝的方法常見的有兩種，Reduced-Error Pruning（REP，錯誤率降低剪枝）、Pessimistic Error Pruning（PEP，悲觀剪枝），下面分別介紹。

錯誤率降低剪枝：

這個演算法的思路是，再用一個測試資料集來糾正完全決策樹。對於完全決策樹的每一個非葉子節點的子樹，嘗試把它替換成一個葉子節點，該葉子節點的類別，用子樹所覆蓋訓練樣本中存在最多的那個類來代替。這就得到了一個簡化決策樹，然後比較這兩個決策樹在測試資料集中的表現，如果優於原來的決策樹，則保留修改。自下而上的遍歷所有子樹，直至沒有任何子樹需要替換。

悲觀剪枝：

該演算法是用過極小化損失函式實現的，設樹T的葉節點個數為|T|，t是樹T的葉節點，該葉節點有Nt個樣本點，其中k類的樣本點有Ntk個，k=1,2...K, H(T)為葉節點t的熵，α≥0為引數，則損失函式定義為，

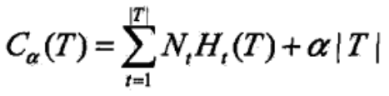
 將上式簡記為，

其中，C(T)表示決策樹與訓練資料的擬合度，|T|表示決策樹的複雜度，α控制兩者之間的影響。α越大，決策樹越簡單，α越小，決策樹越複雜。

假設輸入輸出如下：

輸入：完全樹T，引數α

輸出：修剪後的子樹Tα

則剪枝的方法如下，

(1)、計算每個節點的熵

(2)、遞迴的從樹的葉節點向上回縮。

假設一組葉節點回縮前後的樹分別為TB和TA，則其對應的損失函式值分別為Cα(TB)和Cα(TA)，如果Cα(TA)≤Cα(TB)，則剪枝，將子樹的根節點變成新的葉節點。

(3)、重複第（2）步，直到不能繼續為止。

示意圖如下，

 注：以上圖參考自李航的《統計學習方法》