一、參考

二、

線性迴歸

基本表示：

x:特徵/輸入變數/自變數

y:目標變數/觀測值

h(x):假設/模型/函式

對於特徵x，xi表示該特徵的第i個樣本輸入，xj表示在多特徵迴歸中的第j個特徵，xij表示第j個特徵的第i個樣本輸入。i<=m（樣本數）；j<=n（特徵數）。

單變量回歸模型表示：

      其中x0 = 1

該表示式基於線性迴歸方程原理，為了便於後續表達，將a的係數1用表示

多變數/特徵線性迴歸模型表示

與單變數線性迴歸模型基本一致，只是增加了特徵，並用向量表示；初始向量為列向量；=1。

損失函式表示：均方差/MSE

改表示式基於均方差原理，求各樣本輸出結果與觀察值間差距平方和，用於表示模型的準確度，在模型中，我們的最終目的是通過各種方法調整引數

損失函式求優：梯度下降/Gradient Descent

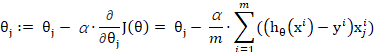
該表示式中:=代表計算機程式中的賦值，模型就是通過不斷賦值調整引數的；

表示 的梯度的一部分，梯度是一個向量，是由損失函式對、、……等n+1個引數求偏導後按序形成的n+1維向量，由於梯度的變化率最大（實在搞不懂如何證明的，姑且認為兼顧了所有維度的切向吧），每個引數減去梯度對應的部分，會使引數下降最快；

注意的是，雖然求偏導及每個更新公式只涉及單獨的，但中包括所有的，所以引數的更新要同時進行，不可以在更新完的值後，將其帶入再更新其他引數（在程式碼實現時一般用中間變數儲存各個引數，當所有引數計算完畢後再一起更新）；

其中α為學習率，代表每次沿梯度下降的幅度，雖然從整體上講，由於偏導數的存在，會使引數在接近最優解時更新變慢，但是仍然存在α設定過小，整體更新慢，α設定過大，在最優解附近徘徊，無法收斂的問題。

由於每次更新需要用到所有樣本，這個更新方法在梯度下降中也稱為批量梯度下降。