從2018年10月份，開始接觸小波變換，從網上查了很多資料，有幾個部落格講得很生動形象，學到了很多，今天在這裡總結一下。

在最一開始，最困擾我的，也是我最想去了解的，就是為什麼要用小波變換而不用傅立葉變換。

後來才知道，我們在實際應用中分析訊號的時候，不僅僅需要知道這個訊號的頻率分佈，還需要知道這個頻率所對應的時間。根據這個需求，我們才採取的小波變換，具體原因就是接下來介紹的內容。

• 在介紹小波的時候，首先先介紹一下傅立葉變換。 傅立葉變換是一種從時域到頻域的變換，通過傅立葉變換，我們可以在知道一個訊號的頻率分佈。然而，當我們拿到這個頻率分佈的時候，我們卻不能將頻率和時域對應起來。這裡打個比方：
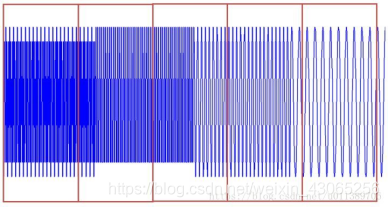
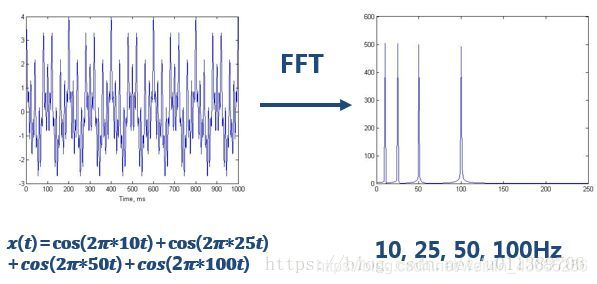  從上圖可知，這個訊號的頻率集中在10Hz,25Hz，50Hz,100Hz 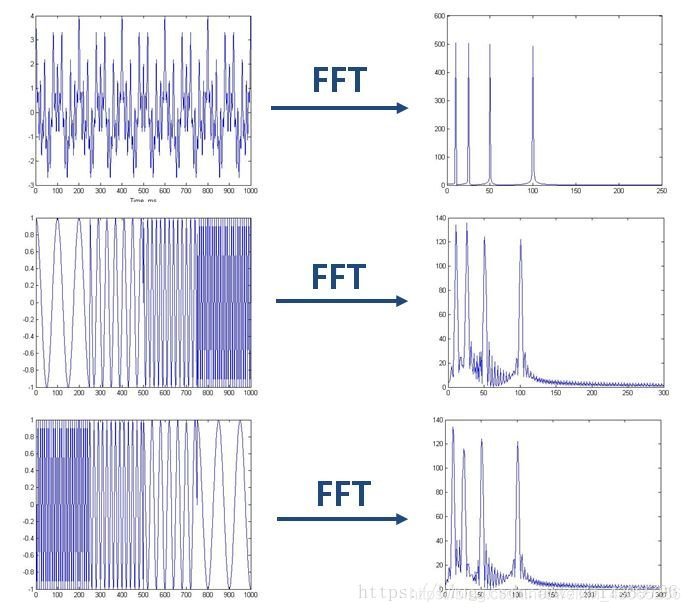而從上面這幅圖中，我們可以看到這三個訊號的頻率成分基本一樣，但他們對應頻率的訊號出現的時間卻不同。

所以，對於非平穩訊號來講，我們單純的使用傅立葉變換，是沒辦法得到頻率和時間的對應關係的。

• 其實傅立葉還有另一個弊端，就是對於突變訊號，傅立葉需要很多餘弦函式來擬合。

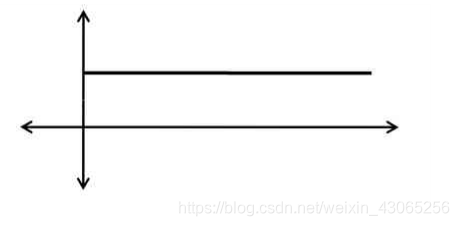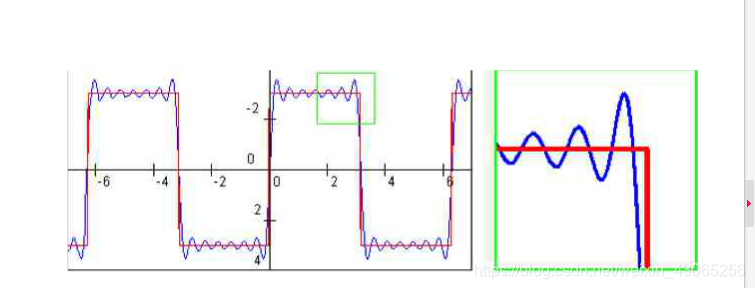
上圖訊號的頻譜，是一個衝擊函式，也就是他的頻譜可以用一個值δ來表示。 但如果是下圖這個突變訊號訊號， 他的頻譜圖確卻是一個類似反函式的圖象，也就是他需要很多很多正弦函式來擬合。 這也就導致了：1.數值過多，計算量較大。 2.第二個就是傅立葉變換的吉布斯現象，對於突變訊號，傅立葉很難擬合得過來。

• 講到這裡，有同學會響，那把訊號分成幾段，再對每一段進行傅立葉變換，這樣就能知道每一個頻率大概出現的時間段了。 這個做法叫，短時傅立葉變換。 也就是對訊號進行加窗處理。

每一個窗內是個大致平穩的過程，經短時傅立葉變換之後，我們可以得到一下一副三維圖，即每個一時間，每一個頻率，所對應的幅值。

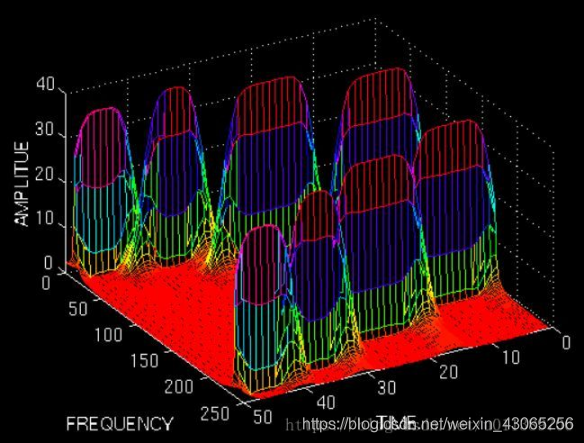但此時問題又出現了，我們怎麼去定義這個窗長呢，如果定義的太長，那就不能真正做到頻率和時間相對應，如果寬太窄，就無法分辨頻率的大小。

• 綜上弊端，我們採用的是小波變換。小波變換和傅立葉變換的不同點，就是傅立葉使用的是正弦函式，而小波變換用的是不同的波，他的波可以有很多種。

（小波(Wavelet)這一術語，顧名思義，“小波”就是小的波形。所謂“小”是指它具有衰減性；而稱之為“波”則是指它的波動性，其振幅正負相間的震盪形式。）

小波是在區間上積分等於0 的波。

簡單講了這些，我們回到最開始的問題， 對於這個突變訊號，如果傅立葉變換，我們需要用很多正餘弦函式來擬合，但如果採用小波變換呢。

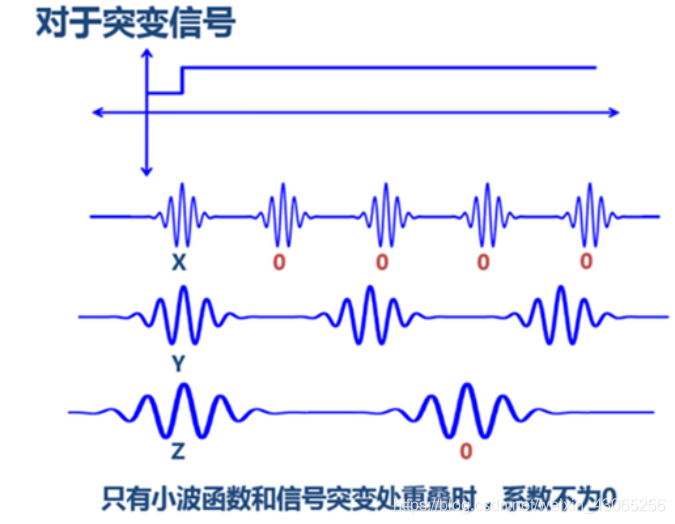
因為小波在區間上的積分為0 ，那麼乘以一個常數，他的積分也等於0 ，所以整個訊號，他其實可以只用突變訊號所積得的X,Y,Z來表達。

轉至https://blog.csdn.net/u011389706/article/details/79544358