今天我們要講的是最長上升子序列（LIS）。

【題目描述】

給定N個數，求這N個數的最長上升子序列的長度。

【樣例輸入】

7

2 5 3 4 1 7 6

【樣例輸出】

4

什麼是最長上升子序列？ 就是給你一個序列，請你在其中求出一段不斷嚴格上升的部分，它不一定要連續。

就像這樣：2,3,4,7和2,3,4,6就是序列2 5 3 4 1 7 6的兩種選取方案。最長的長度是4.

那麼，怎麼求出它的最大上升子序列長度為4呢？這裡介紹兩種方法，都是以動態規劃為基礎的。

首先，我們先介紹較慢（O（n2n2））的方法。我們記num為到這個數為止，最長上升子序列的長度。

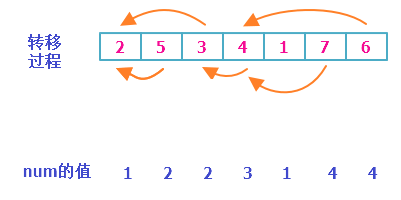
這種方法就是每一次尋找“可以接下去的”，換句話說，設原序列為a，則

當aj<ai(j<i)aj<ai(j<i)且numj+1>numinumj+1>numi時，numi=numj+1numi=numj+1。

對於每一個數，他都是在“可以接下去”的中，從前面的最優值+1轉移而來。

因此，這個演算法是可以求出正確答案的。複雜度很明顯，外層i列舉每個數，內層j列舉目前i的最優值，即O（n2n2）。

那麼，有沒有更快的方法呢？當然有。這回要用到二分。

我們回想一下，在上面O（n2n2）的程式中，哪些地方看起來比較費時？

沒錯，就是內層用於更新i的迴圈。因為每一次他都要查詢一遍，效率並不高。

回到題目，我們發現，他只要我們求長度，所以？

我們可以模擬一個棧。

所以每遇到一個比棧頂元素大的數，就放進棧裡，遇到比棧頂元素小的就二分查詢前邊的元素，找到一個“最應該被換掉的元素”，用新數去更新前邊的元素。

這個演算法不難證明也是正確的。因為前面每一次的列舉都換成了二分，內層的複雜度從nn降到了log2log2，外層不變。所以總的複雜度是O(nlog2nnlog2n)。

#include<cstdio> const int MAX=1001; int a[MAX]; int lis(int x) {     int num[MAX];     for(int i=0;i<x;i++)     {         num[i]=1;         for(int j=0;j<i;j++)         {             if(a[j]<a[i]&&num[j]+1>num[i])                    num[i]=num[j]+1;         }     }     int maxx=0;     for(int i=0;i<x;i++)         if(maxx<num[i])             maxx=num[i];     return maxx; } int main() {     int n;     scanf("%d",&n);     for(int i=0;i<n;i++)         scanf("%d",&a[i]);     return !printf("%d\n",lis(n)); }