動態規劃——陣列中最長遞減子序列
阿新 • • 發佈:2019-01-30
-----Edit by ZhuSenlin HDU
求一個數組的最長遞減子序列比如{9,4,3,2,5,4,3,2}的最長遞減子序列為{9,5,4,3,2}
分析:典型的動態規劃題目,對每一個數計算由它開始的最大遞減子序列的個數,並存放到一張對映表中。例如對陣列a[n]有

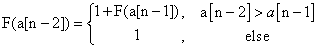
……
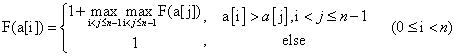
然後利用求得的對映表及最大子序列個數獲取原陣列中的元素。對於{9,4,3,2,5,4,3,2}我們求得最大子序列個數為nMaxLen=5,表為pTable={5,3,2,1,4,3,2,1}。那麼pTable中以此找出nMaxLen,nMaxLen-1,…,1對應的原陣列的值即為最大遞減子序列。對應的為{9,5,4,3,2}.複雜度為O(n2
程式碼如下
#include <iostream> #include <cstring> using namespace std; int Fun(int aIn[],int pTable[],int nLen) { int nMaxLen = 0; for(int i = nLen-1; i >= 0; --i) { int nMax = 0; for(int j = i+1; j < nLen; ++j) { if(aIn[j] < aIn[i]) { nMax = nMax < pTable[j] ? pTable[j] : nMax; } } pTable[i] = 1+nMax; nMaxLen = nMaxLen<pTable[i] ? pTable[i] : nMaxLen; } return nMaxLen; } void PrintMaxSubsequence(int aIn[], int pTable[], int nMaxLen, int nLen) { for(int i = 0,j=0; i < nLen; ++i) { if(pTable[i] == nMaxLen){ cout << aIn[i] << " "; nMaxLen--; } } cout << endl; }
測試程式碼如下:
int main() { int aIn[] = {9,4,3,2,5,4,3,2}; int nLen = sizeof(aIn)/sizeof(int); int* pTable = new int[nLen]; memset(pTable,0,nLen*sizeof(int)); int nMaxLen = Fun(aIn,pTable,nLen); cout << nMaxLen << endl; PrintMaxSubsequence(aIn,pTable,nMaxLen,nLen); delete [] pTable; return 0; }
