本章內容：

• 學習如何處理沒有快速演算法的問題（NP完全問題）。
• 學習近似演算法，使用它們找到NP問題的近似解。
• 學習貪婪策略。

(1)揹包問題

假設你是個貪婪的小偷，揹著可裝35磅重東西的揹包，在商場伺機盜竊各種可裝入揹包的商品。你力圖往揹包中裝入價值最高的商品，你會使用哪種演算法呢？你可使用貪婪策略：先盜竊可裝入揹包的最貴商品，再盜竊還可裝入揹包的最貴商品。但是此次這種貪婪策略可不好使了，例如，你可盜竊的商品有下面三種。

你的揹包可裝入35磅的東西，音響再貴，你把它給偷了，但揹包沒有空間裝其他東西了。

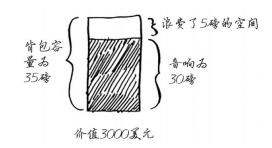
你偷到了價值3000美元的東西。且慢！如果不是偷音響，而是投膝上型電腦和吉他，總價值為3500美元！

在這裡，貪婪策略顯然不能獲得最優解，但非常接近。下一章將介紹如何找出最優解。

（2）集合覆蓋問題

假設你辦了個廣播節目，要讓全美50個州的聽眾都收聽的到。為此，你需要決定在哪些廣播臺播出。在每個廣播臺播出都需要支付費用，因此你力圖在儘可能少的廣播臺播出。現有廣播臺名單和每個廣播臺覆蓋的區域。

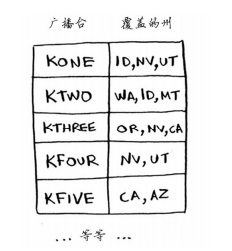
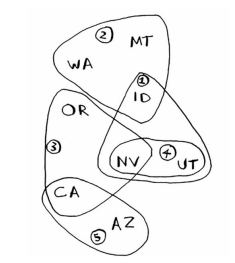
如何找出覆蓋全美50個州的最小廣播臺集合？解法為列出所有可能的集合，在這些集合中選出覆蓋全美50個州的最小集合。我們需要計算每個可能的子集需要的時間。這非常耗時。

近似解法：

1. 選出這樣一個廣播臺，即它覆蓋了最多的未覆蓋州。即便這個廣播臺覆蓋了一些已覆蓋的州，也沒有關係。
2. 重複第一步，直到覆蓋了所有的州。 

這是一種近似演算法。判斷近似演算法優劣的標準如下：

1. 速度有多快；
2. 得到的近似解與最優解的接近程度。

下面來看看解決這個問題的程式碼。

# You pass an array in, and it gets converted to a set.
states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"])

stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])

final_stations = set()

while states_needed:
  best_station = None
  states_covered = set()
  #一次for迴圈找出最佳best_station,知道states_needed為空
  for station, states in stations.items():
    covered = states_needed & states
    if len(covered) > len(states_covered):
      best_station = station
      states_covered = covered

  states_needed -= states_covered
  final_stations.add(best_station)

print(final_stations)
 

（4）NP完全問題

旅行商問題，旅行商需要前往5個不同的城市，他需要找出前往這5個城市的最短路徑。為此，必須計算每條可能的路徑。

前往5個城市時，可能的路徑有120條。這就是NP完全問題，需要計算所有可能的路徑。

如何識別NP完全問題：

NP完全問題無處不在！如果能夠判斷一個問題屬於NP完全問題，就不用去尋找完美的解決方案！而是使用近似演算法即可。以下條件可幫助判斷問題是不是NP完全問題。

• 元素較少時演算法的執行速度非常快，但隨著元素數量的增加，速度會變得非常慢。
• 涉及“所有組合”的問題通常是NP完全問題。
• 不能將問題分成小問題，必須考慮各種可能的情況。這可能是NP完全問題。
• 如果問題涉及序列（如旅行商問題中的城市序列）且難以解決，它可能就是NP完全問題。
• 如果問題涉及集合（如廣播臺集合）且難以解決，它可能就是NP完全問題。
• 如果問題可轉換為集合覆蓋問題或旅行商問題，那它肯定是NP完全問題。

（5）小結

• 貪婪演算法尋找區域性最優解，企圖以這種方式獲得全域性最優解。
• 對於NP完全問題，還沒有找到快速解決的方案。
• 面臨NP完全問題時，最佳的做法是使用近似演算法。
• 貪婪演算法易於實現，執行速度快，是不錯的近似演算法。