整理一下之前看過的內容，方便後面忘記時查詢。

談談深度學習中的 Batch_Size

Batch_Size（批尺寸）是機器學習中一個重要引數，涉及諸多矛盾，下面逐一展開。

首先，為什麼需要有 Batch_Size 這個引數？ Batch 的選擇，首先決定的是下降的方向。如果資料集比較小，完全可以採用全資料集 （Full Batch Learning ）的形式，這樣做至少有 2 個好處：其一，由全資料集確定的方向能夠更好地代表樣本總體，從而更準確地朝向極值所在的方向。其二，由於不同權重的梯度值差別巨大，因此選取一個全域性的學習率很困難。 Full Batch Learning 可以使用Rprop 只基於梯度符號並且針對性單獨更新各權值。

對於更大的資料集，以上 2 個好處又變成了 2 個壞處：其一，隨著資料集的海量增長和記憶體限制，一次性載入所有的資料進來變得越來越不可行。其二，以 Rprop 的方式迭代，會由於各個 Batch 之間的取樣差異性，各次梯度修正值相互抵消，無法修正。這才有了後來RMSProp 的妥協方案。

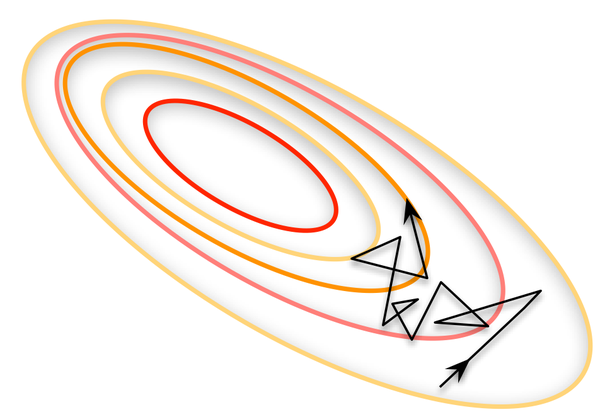
既然 Full Batch Learning 並不適用大資料集，那麼走向另一個極端怎麼樣？ 所謂另一個極端，就是每次只訓練一個樣本，即 Batch_Size = 1。這就是線上學習（Online Learning）。線性神經元在均方誤差代價函式的錯誤面是一個拋物面，橫截面是橢圓。對於多層神經元、非線性網路，在區域性依然近似是拋物面。使用線上學習，每次修正方向以各自樣本的梯度方向修正，橫衝直撞各自為政，難以達到收斂。 

可不可以選擇一個適中的 Batch_Size 值呢？ 當然可以，這就是批梯度下降法（Mini-batches Learning）。因為如果資料集足夠充分，那麼用一半（甚至少得多）的資料訓練算出來的梯度與用全部資料訓練出來的梯度是幾乎一樣的。

批訓練引入最大的好處是針對非凸損失函式（凸函式就是U型函式）來做的，畢竟非凸的情況下，全樣本就算工程上的動，也會卡在區域性最優上，批表示了全樣本的部分抽樣實現，相當於認為引入修正梯度上的取樣噪聲，使“一路不通找別路”更有可能的搜尋最優值。

在合理範圍內，增大 Batch_Size 有何好處？

• 記憶體利用率提高了，大矩陣乘法的並行化效率提高。
• 跑完一次 epoch（全資料集）所需的迭代次數減少，對於相同資料量的處理速度進一步加快。
• 在一定範圍內，一般來說 Batch_Size 越大，其確定的下降方向越準，引起訓練震盪越小。

盲目增大 Batch_Size 有何壞處？

• 記憶體利用率提高了，但是記憶體容量可能撐不住了。
• 跑完一次 epoch（全資料集）所需的迭代次數減少，要想達到相同的精度，其所花費的時間大大增加了，從而對引數的修正也就顯得更加緩慢。
• Batch_Size 增大到一定程度，其確定的下降方向已經基本不再變化。

訓練：

若全集有502張圖片，引數batch_size=30,則訓練一次全集需要跑502/32=15次，epoch是訓練全集的次數，epoch=100即訓練100次全集。

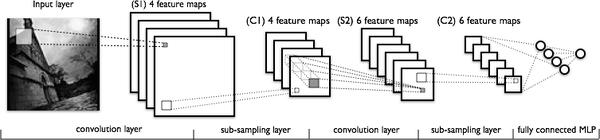
調節 Batch_Size 對訓練效果影響到底如何？ 這裡跑一個 LeNet 在 MNIST 資料集上的效果。MNIST 是一個手寫體標準庫，我使用的是 Theano 框架。這是一個 Python 的深度學習庫。安裝方便（幾行命令而已），除錯簡單（自帶 Profile），GPU / CPU 通吃，官方教程相當完備，支援模組十分豐富（除了 CNNs，更是支援 RBM / DBN / LSTM / RBM-RNN / SdA / MLPs）。在其上層有 Keras 封裝，支援 GRU / JZS1, JZS2, JZS3 等較新結構，支援 Adagrad / Adadelta / RMSprop / Adam 等優化演算法。 

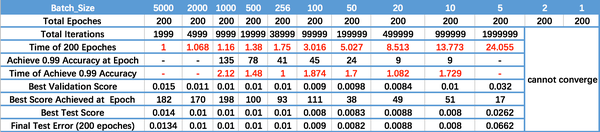
執行結果如上圖所示，其中絕對時間做了標么化處理。執行結果與上文分析相印證：

• Batch_Size 太小，演算法在 200 epoches 內不收斂。
• 隨著 Batch_Size 增大，處理相同資料量的速度越快。
• 隨著 Batch_Size 增大，達到相同精度所需要的 epoch 數量越來越多。
• 由於上述兩種因素的矛盾， Batch_Size 增大到某個時候，達到時間上的最優。
• 由於最終收斂精度會陷入不同的區域性極值，因此 Batch_Size 增大到某些時候，達到最終收斂精度上的最優。

       深度神經網路的優化是個nonconvex problem.所以基於SGD的訓練batch size不能取過大。過大的batchsize的結果是網路很容易收斂到一些不好的區域性最優點。。同樣太小的batch也存在一些問題，比如訓練速度很慢，訓練不容易收斂等。。具體的batch size的選取和訓練集的樣本數目相關。。舉個例子，比如在3小時的語音識別庫（大約108萬個樣本）訓練DNN,通常batch 取128..而在300小時的庫上會取1024.

對weight decay、momentum和normalization的一些理解

一、weight decay（權值衰減）的使用既不是為了提高收斂精確度也不是為了提高收斂速度，其最終目的是防止過擬合。在損失函式中，weight decay是放在正則項（regularization）前面的一個係數，正則項一般指示模型的複雜度，所以weight decay的作用是調節模型複雜度對損失函式的影響，若weight decay很大，則複雜的模型損失函式的值也就大。

  這個式子在下面的正則化中會詳細講解，其中就是前面說的weight decay 

二、momentum是梯度下降法中一種常用的加速技術。

對於一般的SGD，其表示式為,沿負梯度方向下降。學習率

而帶momentum項的SGD則寫生如下形式： 其中即momentum係數，通俗的理解上面式子就是，如果上一次的momentum（即）與這一次的負梯度方向是相同的，那這次下降的幅度就會加大，所以這樣做能夠達到加速收斂的過程。

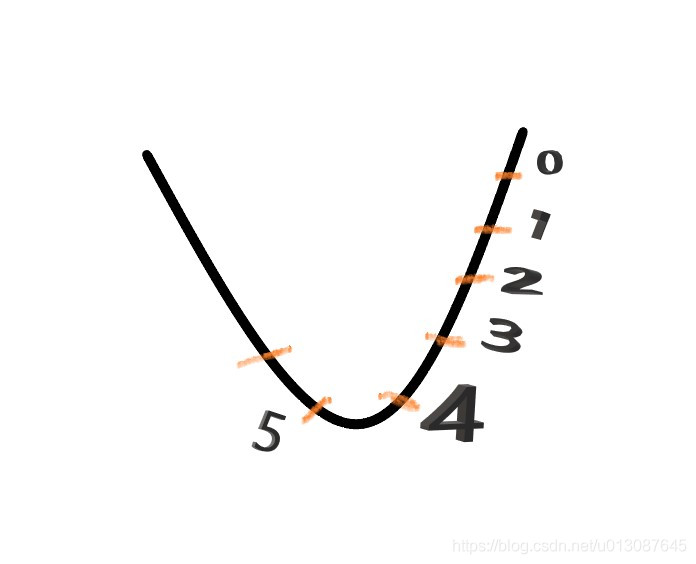
如上圖所示，在剛開始的時候為0，也就是沒有動量，從1到2時和從0到1的負梯度方向相同則這次的動量就會加大，就有可能到達3這樣就會在下降方向加快收斂。若從4到5發現動量方向和從3到4不同則到達5的時候就會減弱梯度，減小擺動加快收斂。

三、batch normalization的是指在神經網路中啟用函式的前面，將按照特徵進行normalization，這樣做的好處有三點： 1、提高梯度在網路中的流動。Normalization能夠使特徵全部縮放到[0,1]，這樣在反向傳播時候的梯度都是在1左右，避免了梯度消失現象。 2、提升學習速率。歸一化後的資料能夠快速的達到收斂。 3、減少模型訓練對初始化的依賴。

L1和L2正則化

先看一下知乎的一段解答來了解一下基本的知識

r(d)可以理解為有d的引數進行約束，或者 D 向量有d個維度。 咱們將樓主的給的凸優化結構細化一點，別搞得那麼抽象，不好解釋；

, 其中， 咱們可以令: f() = .

ok，這個先介紹到這裡，至於f(x)為什麼用多項式的方式去模擬？相信也是很多人的疑問，很簡單，大家看看高等數學當中的泰勒展開式就行了，任何函式都可以用多項式的方式去趨近，log x,lnx,等等都可以去趨近，而不同的函式曲線其實就是這些基礎函式的組合，理所當然也可以用多項式去趨近，好了，這個就先解釋到這裡了。

接下來咱們看一下擬合的基礎概念。 首先，用一個例子來理解什麼是過擬合，假設我們要根據特徵分類{男人X，女人O}。 請看下面三幅圖，x1、x2、x3；

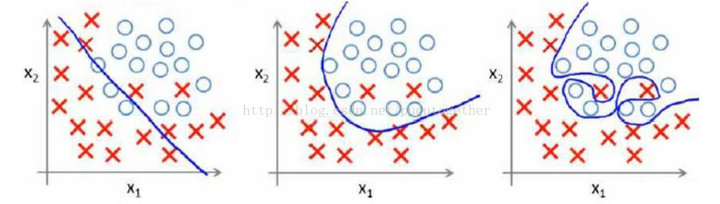
這三幅圖很容易理解： 1、 圖x1明顯分類的有點欠缺，有很多的“男人”被分類成了“女人”。 2、 圖x2雖然有兩個點分類錯誤，但是能夠理解，畢竟現實世界有噪音干擾，比如有些人男人留長髮、化妝、人妖等等。 3、 圖x3分類全部是正確的，但是看著這副圖片，明顯覺得過了，連人妖都區分的出來，可想而知，學習的時候需要更多的引數項，甚至將生殖器官的形狀、喉結的大小、有沒有鬍鬚特徵等都作為特徵取用了，總而言之f(x)多項式的N特別的大，因為需要提供的特徵多，或者提供的測試用例中我們使用到的特徵非常多(一般而言，機器學習的過程中，很多特徵是可以被丟棄掉的)。

好了，總結一下三幅圖： x1我們稱之為【欠擬合】 x2我們稱之為【分類正擬合】，隨便取的名字，反正就是容錯情況下剛好的意思。 x3我們稱之為【過擬合】，這種情況是我們不希望出現的狀況，為什麼呢？很簡單，它的分類只是適合於自己這個測試用例，對需要分類的真實樣本而言，實用性可想而知的低。

恩，知道了過擬合是怎麼回事之後，我們來看一下如何去規避這種風險。先不管什麼書上說的、老師講的、經驗之說之類的文言文。咱們就站在第一次去接觸這種分類模型的角度去看待這個問題，發散一下思維，我們應該如何去防止過擬合？顯而易見，我們應該從【過擬合】出現的特徵去判別，才能規避吧？顯而易見，我們應該、而且只能去看【過擬合】的f(x)形式吧？顯而易見，我們從【過擬合】的圖形可以看出f(x)的涉及到的特徵項一定很多吧，即等等很多吧？顯而易見，N很大的時候，是等數量增長的吧？顯而易見，w係數都是學習來的吧？

So，現在知道這些資訊之後，如何去防止過擬合，我們首先想到的就是控制N的數量吧，即讓N最小化吧，而讓N最小化，其實就是讓W向量中項的個數最小化吧？ 其中，W=()

PS: 可能有人會問，為什麼是考慮W，而不是考慮X?很簡單，你不知道下一個樣本想x輸入的是什麼，所以你怎麼知道如何去考慮x呢？相對而言，在下一次輸入,即第k個樣本之前，我們已經根據次測試樣本的輸入，計算(學習)出了W.就是這麼個道理，很簡單。

我們再來思考，如何求解“讓W向量中項的個數最小化”這個問題，學過數學的人是不是看到這個問題有點感覺？對，沒錯，這就是0範數的概念！什麼是範數，我在這裡只是給出個0-2範數定義，不做深究，以後有時間在給大家寫點文章去分析範數的有趣玩法；0範數，向量中非零元素的個數。 1範數，為絕對值之和。 2範數，就是通常意義上的模。

PS，貌似有人又會問，上面不是說求解“讓W向量中項的個數最小化”嗎？怎麼與0範數的定義有點不一樣，一句話，向量中0元素，對應的x樣本中的項我們是不需要考慮的，可以砍掉。因為沒有啥意義，說明項沒有任何權重。so，一個意思啦。

r(d) = “讓W向量中項的個數最小化” =

所以為了防止過擬合，咱們除了需要前面的相加項最小，即樓主公式當中的 =  （支出向量機的目標函式）最小，我們還需要讓r(d)=最小，所以，為了同時滿足兩項都最小化，咱們可以求解讓和r(d)之和最小，這樣不就同時滿足兩者了嗎？如果r(d) 過大，再小也沒用；相反r(d)再小，太大也失去了問題的意義。 說到這裡我覺得樓主的問題我已經回答了，那就是為什麼需要有個r(d)項，為什麼r(d)能夠防止過擬合原因了。  

書本中，或者很多機器學習的資料中，為了讓全球的機器學習人員有個通用的術語，同時讓大家便於死記硬本，給我上一段黑體字的部分的內容加上了一坨定義，例如： 我們管叫做經驗風險，管上面我們思維導圖的過程叫做正則化，所以順其自然的管r(d)叫做正則化項，然後管+r(d) 叫做結構風險，所以順其自然的正則化就是我們將結構風險最小化的過程，它們是等價的。 By the way，各位計算機界的叔叔、阿姨、伯伯、嬸嬸，經過不懈的努力，發現了這個公式很多有意思的地方，它們發現0範數比較噁心，很難求，求解的難度是個NP完全問題。然後很多腦袋瓜子聰明的叔叔、阿姨、伯伯、嬸嬸就想啊，0範數難求，咱們就求1範數唄，然後就研究出了下面的等式：

一定的條件我就不解釋了，這裡有一堆演算法，例如主成分KPCA等等，例子我就不在舉了，還是原話，以後我會盡量多寫點這些演算法生動點的推到過程，很簡單，注重過程，不要死記硬背書本上的結果就好。 上面概括而言就是一句話總結：1範數和0範數可以實現稀疏，1因具有比L0更好的優化求解特性而被廣泛應用。然後L2範數，是下面這麼理解的，我就直接查別人給的解釋好了，反正簡單，就不自己動腦子解釋了：L2範數是指向量各元素的平方和然後求平方根。我們讓L2範數的正則項||W||2最小，可以使得W的每個元素都很小，都接近於0，但與L1範數不同，它不會讓它等於0，而是接近於0，這裡是有很大的區別的哦；所以大家比起1範數，更鐘愛2範數。 所以我們就看到書籍中，一來就是，r(d)= 或者r(d)= 這種結構了，然後在機器學習當中還能看到下面的結構： min{ } ，>=0 都是這麼來的啦，萬變不離其中。

接下來看另一段解答：

噪聲，是指那些不能代表資料真實特性的資料點，它們的生成是隨機的。學習和捕捉這些資料點讓你的模型複雜度增大，有過擬合的風險。

避免過擬合的方式之一是使用交叉驗證（cross validation），這有利於估計測試集中的錯誤，同時有利於確定對模型最有效的引數。本文將重點介紹一種方法，它有助於避免過擬合併提高模型的可解釋性。

                                                             正則化

正則化是一種迴歸的形式，它將係數估計（coefficient estimate）朝零的方向進行約束、調整或縮小。也就是說，正則化可以在學習過程中降低模型複雜度和不穩定程度，從而避免過擬合的危險。

一個簡單的線性迴歸關係如下式。其中 Y 代表學習關係，β 代表對不同變數或預測因子 X 的係數估計。

Y ≈ β0 + β1X1 + β2X2 + …+ βpXp

擬合過程涉及損失函式，稱為殘差平方和（RSS）。係數選擇要使得它們能最小化損失函式。

  就是上面的預測Y

這個式子可以根據你的訓練資料調整係數。但如果訓練資料中存在噪聲，則估計的係數就不能很好地泛化到未來資料中。這正是正則化要解決的問題，它能將學習後的引數估計朝零縮小調整。

嶺迴歸

上圖展示了嶺迴歸（Ridge Regression）。這一方法通過新增收縮量調整殘差平方和。現在，係數要朝最小化上述函式的方向進行調整和估計。其中，λ 是調整因子，它決定了我們要如何對模型的複雜度進行「懲罰」。模型複雜度是由係數的增大來表現的。我們如果想最小化上述函式，這些係數就應該變小。這也就是嶺迴歸避免係數過大的方法。同時，注意我們縮小了每個變數和響應之間的估計關聯，除了截距 β0 之外——這是因為，截距是當 xi1 = xi2 = …= xip = 0 時對平均值的度量。

當 λ=0 時，懲罰項沒有作用，嶺迴歸所產生的引數估計將與最小二乘法相同。但是當 λ→∞ 時，懲罰項的收縮作用就增大了，導致嶺迴歸下的係數估計會接近於零。可以看出，選擇一個恰當的 λ 值至關重要。為此，交叉驗證派上用場了。由這種方法產生的係數估計也被稱為 L2 範數（L2 norm）。

標準的最小二乘法產生的係數是隨尺度等變的（scale equivariant）。即，如果我們將每個輸入乘以 c，那麼相應的係數需要乘以因子 1/c。因此，無論預測因子如何縮放，預測因子和係數的乘積（X{β}）保持不變。但是，嶺迴歸當中卻不是如此。因此，我們需要在使用嶺迴歸之前，對預測因子進行標準化，即將預測因子轉換到相同的尺度。用到的公式如下：

Lasso 迴歸

Lasso 是另一個變體，其中需要最小化上述函式。很明顯，這種變體只有在懲罰高係數時才有別於嶺迴歸。它使用 |β_j|（模數）代替 β 的平方作為懲罰項。在統計學中，這被稱為 L1 範數。

讓我們換個角度看看上述方法。嶺迴歸可以被認為是求解一個方程，其中係數的平方和小於等於 s。而 Lasso 可以看作係數的模數之和小於等於 s 的方程。其中，s 是一個隨收縮因子 λ 變化的常數。這些方程也被稱為約束函式。

假定在給定的問題中有 2 個引數。那麼根據上述公式，嶺迴歸的表示式為 β1² + β2² ≤ s。這意味著，在由 β1² + β2² ≤ s 給出的圓的所有點當中，嶺迴歸係數有著最小的 RSS（損失函式）。

同樣地，對 Lasso 而言，方程變為 |β1|+|β2|≤ s。這意味著在由 |β1|+|β2|≤ s 給出的菱形當中，Lasso 係數有著最小的 RSS（損失函式）。

下圖描述了這些方程。

上圖的綠色區域代表約束函式域：左側代表 Lasso，右側代表嶺迴歸。其中紅色橢圓是 RSS 的等值線，即橢圓上的點有著相同的 RSS 值。對於一個非常大的 s 值，綠色區域將會包含橢圓的中心，使得兩種迴歸方法的係數估計等於最小二乘估計。但是，上圖的結果並不是這樣。在上圖中，Lasso 和嶺迴歸係數估計是由橢圓和約束函式域的第一個交點給出的。因為嶺迴歸的約束函式域沒有尖角，所以這個交點一般不會產生在一個座標軸上，也就是說嶺迴歸的係數估計全都是非零的。然而，Lasso 約束函式域在每個軸上都有尖角，因此橢圓經常和約束函式域相交。發生這種情況時，其中一個係數就會等於 0。在高維度時（引數遠大於 2），許多係數估計值可能同時為 0。

這說明了嶺迴歸的一個明顯缺點：模型的可解釋性。它將把不重要的預測因子的係數縮小到趨近於 0，但永不達到 0。也就是說，最終的模型會包含所有的預測因子。但是，在 Lasso 中，如果將調整因子 λ 調整得足夠大，L1 範數懲罰可以迫使一些係數估計值完全等於 0。因此，Lasso 可以進行變數選擇，產生稀疏模型。

正則化有何效果？

標準的最小二乘模型常常產生方差。即對於與訓練集不同的資料集，模型可能不能很好地泛化。正則化能在不顯著增大偏差的的同時，顯著減小模型的方差。因此，正則化技術中使用的調整因子 λ，能控制對方差和偏差的影響。當 λ 的值開始上升時，它減小了係數的值，從而降低了方差。直到上升到某個值之前，λ 的增大很有利，因為它只是減少方差（避免過擬合），而不會丟失資料的任何重要特性。但是在某個特定值之後，模型就會失去重要的性質，導致偏差上升產生欠擬合。因此，要仔細選擇 λ 的值。

這就是你開始使用正則化之前所要掌握的全部基礎，正則化技術能夠幫助你提高迴歸模型的準確性。實現這些演算法的一個很流行的庫是 Scikit-Learn，它可以僅僅用 Python 中的幾行程式碼執行你的模型。

正則化項即罰函式，該項對模型向量進行“懲罰”，從而避免單純最小二乘問題的過擬合問題。正則化項本質上是一種先驗資訊，整個最優化問題從貝葉斯觀點來看是一種貝葉斯最大後驗估計，其中正則化項對應後驗估計中的先驗資訊，損失函式對應後驗估計中的似然函式，兩者的乘積即對應貝葉斯最大後驗估計的形式，如果你將這個貝葉斯最大後驗估計的形式取對數，即進行極大似然估計，你就會發現問題立馬變成了損失函式+正則化項的最優化問題形式。 好，接下來我來舉個例子，就拿Lasso來說吧：Lasso中中的目標函式即相當於如下的後驗概率：

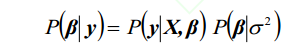
其中

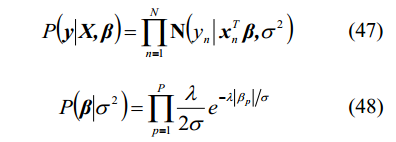
(47)是似然函式，對應於Lasso中的損失函式，(48)是先驗概率，相當於Lasso中的正則化項。可以看出，Lasso的正則化項從貝葉斯觀點來看就是以Laplace先驗資訊。 採用不同的先驗資訊，可得到不同的結果。因此，你可以設計其它的先驗資訊構成新的正則化項。