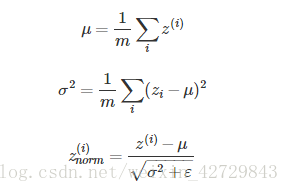目錄

1.超引數除錯

深度神經網路需要除錯的超引數（Hyperparameters）較多，包括：

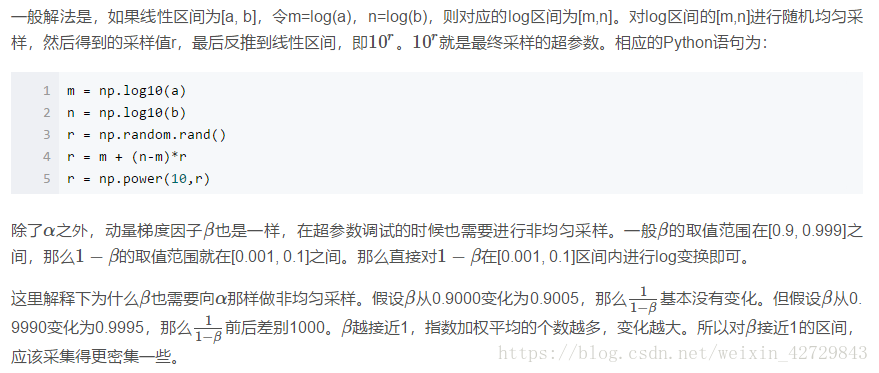
• α：學習因子

• β：動量梯度下降因子

• ：Adam演算法引數

• #layers：神經網路層數

• #hidden units：各隱藏層神經元個數

• learning rate decay：學習因子下降引數

• mini-batch size：批量訓練樣本包含的樣本個數

超引數之間也有重要性差異。通常來說，學習因子αα是最重要的超引數，也是需要重點除錯的超引數。動量梯度下降因子ββ、各隱藏層神經元個數#hidden units和mini-batch size的重要性僅次於α。然後就是神經網路層數#layers和學習因子下降引數learning rate decay。最後，Adam演算法的三個引數β1,β2,ε一般常設定為0.9，0.999和

如何選擇和除錯超引數？

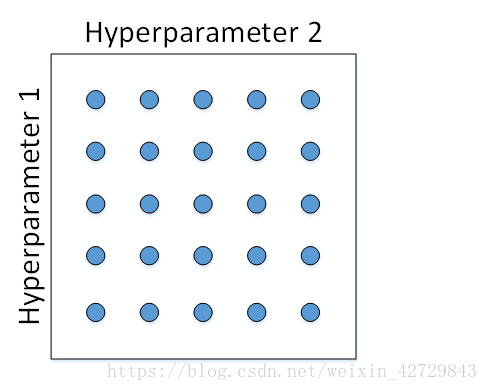
傳統的機器學習中，我們對每個引數等距離選取任意個數的點，然後，分別使用不同點對應的引數組合進行訓練，最後根據驗證集上的表現好壞，來選定最佳的引數。例如有兩個待除錯的引數，分別在每個引數上選取5個點，這樣構成了5x5=25中引數組合,如圖所示：

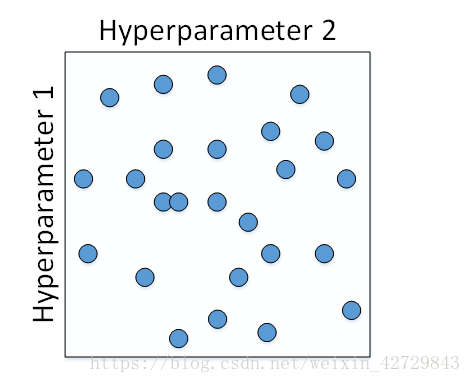
這種做法在引數比較少的時候效果較好。但是在深度神經網路模型中，我們一般不採用這種均勻間隔取點的方法，比較好的做法是使用隨機選擇。也就是說，對於上面這個例子，我們隨機選擇25個點，作為待除錯的超引數，如下圖所示：

隨機化選擇引數的目的是為了儘可能地得到更多種引數組合。還是上面的例子，如果使用均勻取樣的話，每個引數只有5種情況；而使用隨機取樣的話，每個引數有25種可能的情況，因此更有可能得到最佳的引數組合。

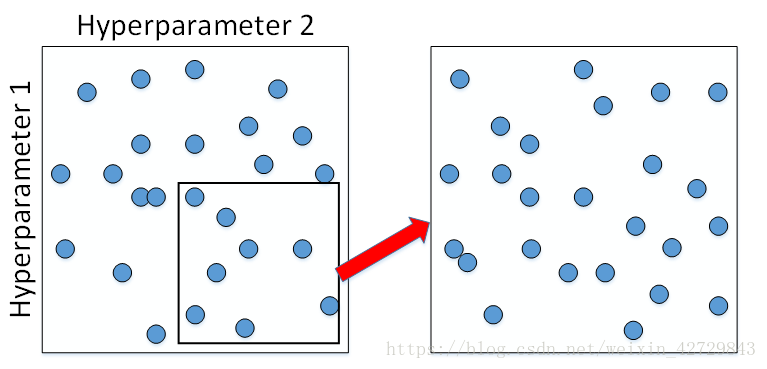
在經過隨機取樣之後，我們可能得到某些區域模型的表現較好。然而，為了得到更精確的最佳引數，我們應該繼續對選定的區域進行由粗到細的取樣（coarse to fine sampling scheme）。也就是放大表現較好的區域，再對此區域做更密集的隨機取樣。例如，對下圖中右下角的方形區域再做25點的隨機取樣，以獲得最佳引數。

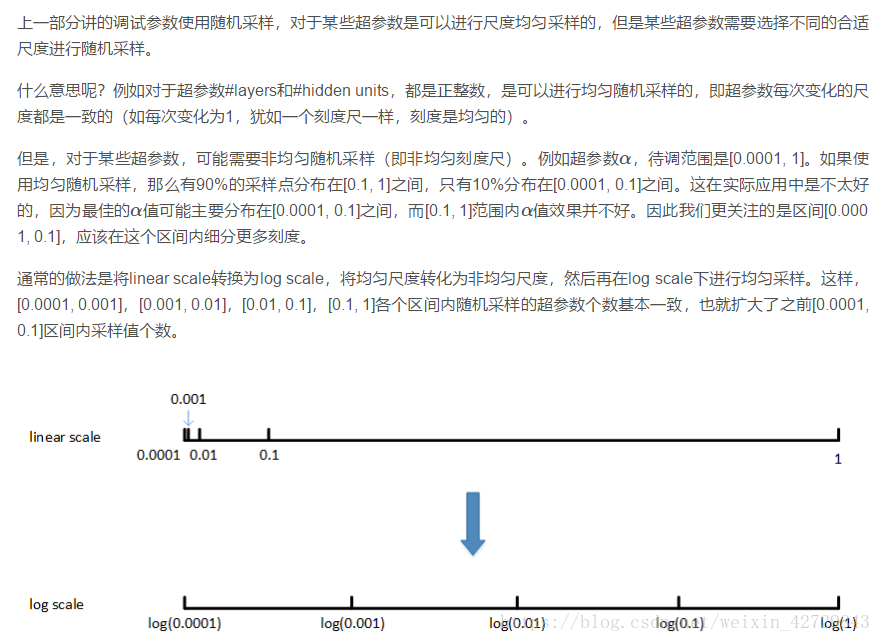
為超引數選擇合適的範圍

經過除錯選擇完最佳的超引數並不是一成不變的，一段時間之後（例如一個月），需要根據新的資料和實際情況，再次除錯超引數，以獲得實時的最佳模型。

超引數訓練的實踐

在訓練深度神經網路時有兩種訓練方式：

一種情況是受計算能力所限或資料量太大，我們只能對一個模型進行訓練，除錯不同的超引數，使得這個模型有最佳的表現。我們稱之為Babysitting one model。類比為熊貓計算Panda approach

另外一種情況是可以對多個模型同時進行訓練，每個模型上除錯不同的超引數，根據表現情況，選擇最佳的模型。我們稱之為Training many models in parallel。類比為魚卵計算Caviar approach

2.Batch 標準化

Batch Normalization不僅可以讓除錯超引數更加簡單，而且可以讓神經網路模型更加“健壯”。也就是說較好模型可接受的超引數範圍更大一些，包容性更強，使得更容易去訓練一個深度神經網路。之前的標準化輸入是對輸入資料進行處理使其均值為0方差為1，那麼對於神經網路對其輸入資料和各隱藏層的輸入進行標準化處理也會加快學習速度。神經網路隱藏層的輸入就是上一層的輸出，假設我們有m個隱藏單元（單個mini-batch中包含的樣本數），我們可以對進行如下的處理：

ε是為了防止分母為零，可取值。這樣，使得該隱藏層的所有輸入z(i)均值為0，方差為1。但是我們並不想讓所有的均值為0方差為1，因此要對進行進一步處理：

其中是用來控制均值和方差的學習引數，可以通過調整這兩個引數的值讓的方差和均值為任意值。

這樣，通過Batch Normalization，對隱藏層的各個，進行標準化處理，得到，替代。

值得注意的是，輸入的標準化處理Normalizing inputs和隱藏層的標準化處理Batch Normalization是有區別的。Normalizing inputs使所有輸入的均值為0，方差為1。而Batch Normalization可使各隱藏層輸入的均值和方差為任意值。實際上，從啟用函式的角度來說，如果各隱藏層的輸入均值在靠近0的區域即處於啟用函式的線性區域，這樣不利於訓練好的非線性神經網路，得到的模型效果也不會太好。這也解釋了為什麼需要用γ和β來對作進一步處理。

Batch Norm為什麼奏效

我們可以把輸入特徵做均值為0，方差為1的規範化處理，來加快學習速度。而Batch Norm也是對隱藏層各神經元的輸入做類似的規範化處理。總的來說，Batch Norm不僅能夠提高神經網路訓練速度，而且能讓神經網路的權重W的更新更加“穩健”，尤其在深層神經網路中更加明顯。比如神經網路很後面的W對前面的W包容性更強，即前面的W的變化對後面W造成的影響很小，整體網路更加健壯。

舉個例子來說明，假如用一個淺層神經網路（類似邏輯迴歸）來訓練識別貓的模型。如下圖所示，提供的所有貓的訓練樣本都是黑貓。然後，用這個訓練得到的模型來對各種顏色的貓樣本進行測試，測試的結果可能並不好。其原因是訓練樣本不具有一般性（即不是所有的貓都是黑貓），這種訓練樣本（黑貓）和測試樣本（貓）分佈的變化稱之為covariate shift。

對於這種情況，如果實際應用的樣本與訓練樣本分佈不同，即發生了covariate shift，則一般是要對模型重新進行訓練的。在神經網路，尤其是深度神經網路中，covariate shift會導致模型預測效果變差，重新訓練的模型各隱藏層的W[l]和B[l]均產生偏移、變化。而Batch Norm的作用恰恰是減小covariate shift的影響，讓模型變得更加健壯，魯棒性更強。Batch Norm減少了各層W[l]、B[l]之間的耦合性，讓各層更加獨立，實現自我訓練學習的效果。也就是說，如果輸入發生covariate shift，那麼因為Batch Norm的作用，對個隱藏層輸出Z[l]Z[l]進行均值和方差的歸一化處理，W[l]和B[l]更加穩定，使得原來的模型也有不錯的表現。針對上面這個黑貓的例子，如果我們使用深層神經網路，使用Batch Norm，那麼該模型對花貓的識別能力應該也是不錯的。

從另一個方面來說，Batch Norm也起到輕微的正則化（regularization）效果。具體表現在：

• 每個mini-batch都進行均值為0，方差為1的歸一化操作

• 每個mini-batch中，對各個隱藏層的Z[l]Z[l]添加了隨機噪聲，效果類似於Dropout

• mini-batch越小，正則化效果越明顯

但是，Batch Norm的正則化效果比較微弱，正則化也不是Batch Norm的主要功能。

測試時的Batch Norm

訓練過程中，Batch Norm是對單個mini-batch進行操作的，但在測試過程中，如果是單個樣本，該如何使用Batch Norm進行處理呢？

首先，回顧一下訓練過程中Batch Norm的主要過程：

其中，μ和σ2是對單個mini-batch中所有m個樣本求得的。在測試過程中，如果只有一個樣本，求其均值和方差是沒有意義的，就需要對μ和σ2進行估計。估計的方法有很多，理論上我們可以將所有訓練集放入最終的神經網路模型中，然後將每個隱藏層計算得到的μ[l]和σ2[l]直接作為測試過程的μ和σ2來使用。但是，實際應用中一般不使用這種方法，而是使用我們之前介紹過的指數加權平均（exponentially weighted average）的方法來預測測試過程單個樣本的μ和σ2。

指數加權平均的做法很簡單，對於第l層隱藏層，考慮所有mini-batch在該隱藏層下的μ[l]和σ2[l]，然後用指數加權平均的方式來預測得到當前單個樣本的μ[l]和σ2[l]。這樣就實現了對測試過程單個樣本的均值和方差估計。最後，再利用訓練過程得到的γ和β值計算出各層的值。

3.Softmax迴歸

訓練Softmax分類器

4.深度學習框架

對於複雜的模型，從零開始不太方便，選擇一個好的深度學習框架很重要

選擇框架的基本準則是;

TensorFlow框架

這裡簡單介紹一下最近幾年比較火的一個深度學習框架：TensorFlow。

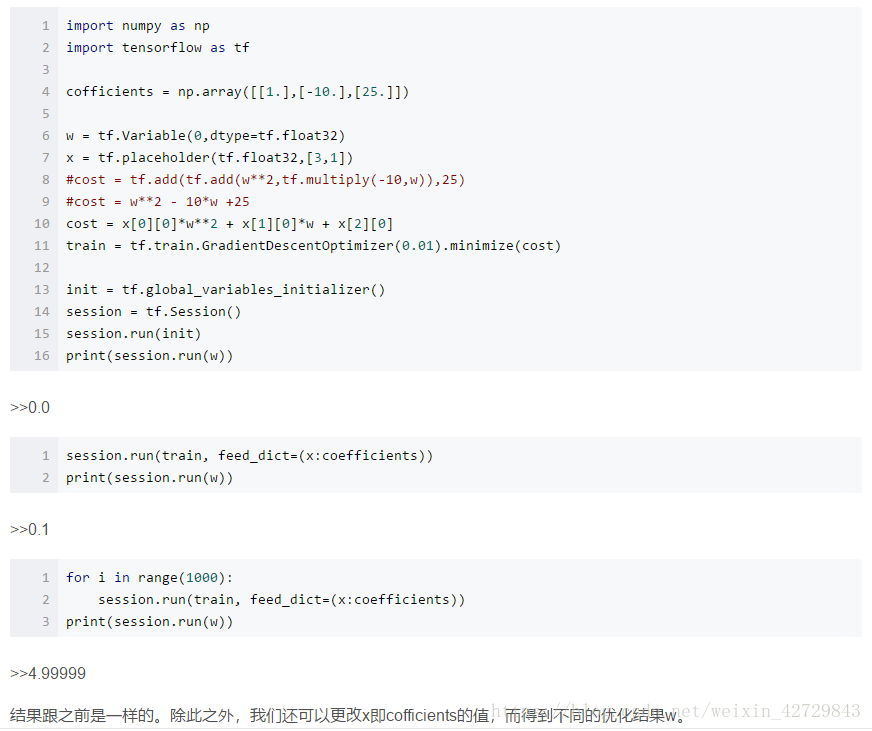
舉個例子來說明，例如cost function是引數w的函式：

如果使用TensorFlow對cost function進行優化，求出最小值對應的w，程式如下：

針對上面這個例子，如果對w前的係數用變數x來代替，程式如下：