 問題描述
現在有一個揹包，這個揹包的容積一定

• 但是現在有n個物品，每個物品都有對應的體積和價值
• 要求如何讓操作才能夠使得我們講儘可能值錢的物品放到這個揹包裡面

 解題思路與演算法思想

• 當看到這道題的時候，我們很自然地會認為這是一個搜尋問題

但是由於當n足夠大的時候,這個搜尋問題的複雜度令人髮指

• 於是我們用動態規劃問題來求這個方法

其實我們可以這個事情抽象成一個決策樹
	這個樹一共有n層，每一層的代表你對放進去還是不放進去某件物品進行決策
這樣就會最終得到2^N種結果
	之後經過觀察我們可以發現，我i們可以反向推到這個決策的過程
	
 

首先明確一點：
	我們選擇的結果和我們選擇的順序無關
		那就就可以從這個樹的最底層網上倒推
	每一個第i行的樹節點之和與相連的兩個第i+1層的樹節點相關，而最底層的樹節點是我們可以事先規定的
		那麼就可以根據公式：f(i,j) = max(f(i+1,j),f(i+1,j-v[i])+w[i]) ;

對於你到底要不要把第i件物品放進去，這和你已經放進去的東西有關

 程式模型的建運用

• 遞推的思路去儲存資訊
• 重點運用好表示式

 資料結構的選用

• 陣列
  核心演算法

 程式設計流程

• 輸入

• 資料錄入

• 進行選擇

• 輸出

 程式設計偽碼演算法

for(int i= n-1 ;i>=0 ;i--)
	{
		for(int j = 0 ;j<sumV ;j++)
		{
			a[i][j] = a[i+1][j] ;
			if(j>=V[i])
			{
					a[i][j] = max(a[i+1][j]  , a[i+1][j-V[i]]+value[i]) ;
			}
		
		}	
	}

 源程式編碼清單

 - `#include<iostream>
#include<algorithm>
#include<vector>
using namespace std ;
int main(void)
{
	vector<int>V ;
	vector<int>value ;
	int sumV ;
	scanf("%d",&sumV) ;//先輸入揹包的體積 
	int n ;
	scanf("%d",&n) ;//輸入物品的個數 
	int tem ;
	for(int i = 0 ;i<n ;i++)
	{
		
		//輸入先是體積，之後是價值 
		scanf("%d",&tem) ;
		V.push_back(tem) ;
		scanf("%d",&tem) ;
		value.push_back(tem) ; 
	}
	// 輸入完成
	
	
	//完成對於記憶陣列的處理 
	
	vector< vector<int> >a ;//總的記憶陣列
	
	vector<int>b ;
	for(int i = 0 ;i<sumV ;i++)
	{
		b.push_back(0) ;
	}
	for(int i = 0 ;i<=n ;i++)
	{
		a.push_back(b) ;
	}
	
	//cout<<a[0][0]<<endl ;
	/*a.resize(n) ;
	for(int i = 0 ;i<n ;i++)
	{
		a[i].resize(sumV) ;
	} */
	 
	 
	//先完成對於陣列的初始化
	for(int j = 0 ;j < sumV; j++)
	{
		a[n][j] = 0 ;//最底層的都是零（因為還沒有開始選擇） 
	}
	
	//之後通過狀態轉移方程得出結論 
	for(int i= n-1 ;i>=0 ;i--)
	{
		for(int j = 0 ;j<sumV ;j++)
		{
			a[i][j] = a[i+1][j] ;
			if(j>=V[i])
			{
					a[i][j] = max(a[i+1][j]  , a[i+1][j-V[i]]+value[i]) ;
			}
		
		}	
	}
	for(int i = 0 ;i<=n ;i++)
	{
		for(int j = 0 ;j<sumV ;j++)
		{
			printf("%d  ",a[i][j]) ;
		}
		printf("\n") ;
	}
		
	int bb = 0 ;
	for(int i = 0 ;i<sumV ;i++) 
	{
		if(a[0][i]>bb)
		{
			bb = a[0][i] ;
		}
	}
	printf("%d",bb) ;
		//	printf("%d",a[0][0]) ;
}`
 

 程式輸入、輸出

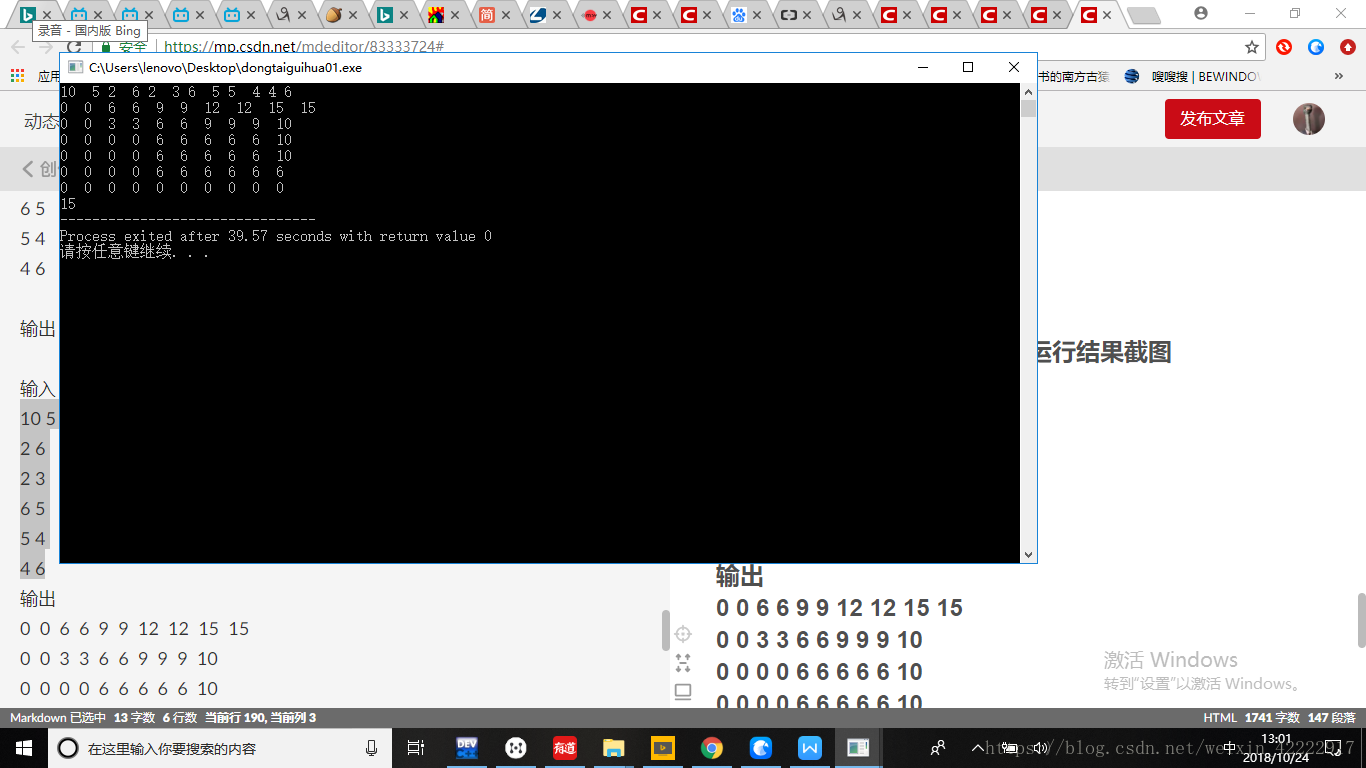
輸入：10 5
10 5
2 6
2 3
6 5
5 4
4 6

輸出：
15

輸入：輸入輸出檔案，或程式執行結果截圖

 時間與空間複雜度分
N^2
 程式使用說明

 總結與完善