LSGAN (Least Squares Generative Adversarial Networks)
1.前言
傳統GAN出現的問題: 傳統GAN, 將Discriminator當作分類器,最後一層使用Sigmoid函式,使用交叉熵函式作為代價函式,容易出現梯度消失和collapse mode等問題,具體原因參考本部落格Wasserstein GAN。
LSGAN主要解決關鍵: 使用最小二乘損失代替交叉熵損失,解決了傳統GAN生成的圖片質量不高以及訓練過程不穩定這倆個缺陷。
為什麼使用最小二乘法能夠改善傳統GAN存在的問題?
1.避免梯度消失
文章指出,傳統的GAN在使用生成的“fake”圖片(已被Discriminator分類為正樣本) 來更新Generator的引數的時候,會造成梯度消失,儘管該生成的"fake"圖片資料離真實樣本的資料還有一定的距離。當使用最小二乘來作為Discriminator的代價函式的時候,最小二乘會將生成的“fake”圖片拉向決策邊界,這裡的決策邊界穿過真實樣本,可以使得LSGANs生成的圖片更接近真實的資料。如文章中下圖所示:
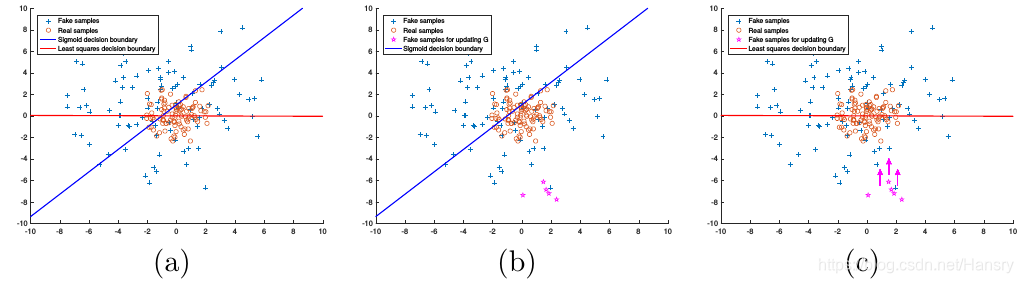
倆種不同損失函式的區別:(a)上圖藍色線代表交叉熵代價函式的Sigmoid決策邊界,紅色線代表最小二乘的決策邊界。值得注意的是,對於成功的GANs學習過程,決策邊界應該穿過真實樣本分佈,除非學習過程已經飽和了。(b)對於Sigmoid 交叉熵損失函式,當生成的“fake”圖片被歸類在決策邊界正確的一邊的時候(correct side),得到的誤差非差小以至於不能更新Generator,儘管這些資料離決策邊界很遠,也即離真實樣本很遠。©最小二乘損失函式會懲罰離決策邊界很遠的資料,使之朝著決策邊界邁進,避免了梯度消失。
2.使訓練過程更加穩定
由於GANs學習過程不穩定導致GANs訓練困難。特別的,對於傳統的由於其存在梯度消失的問題,所以很難更新Generator,造成訓練困難。而LSGANs基於離邊界的距離而對生成的樣本進行懲罰,一定程度上避免了梯度消失,減緩了訓練困難的問題。
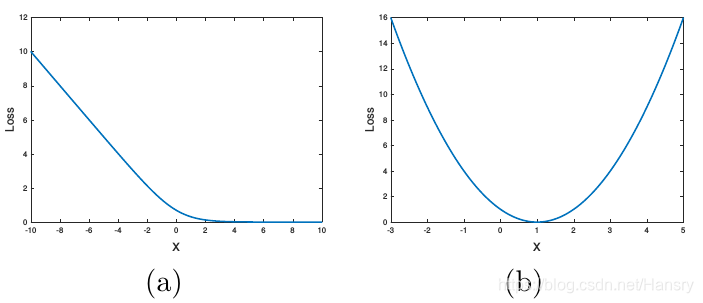
上圖中,(a) 為Sigmoid交叉熵損失函式; (b)為最小二乘損失函式
文章的貢獻:
- 提出最小二乘損失函式,在最小化LSGAN目標函式的時候也在最小化皮爾森散度(Pearson 散度)。
- 設計了倆種LSGANs, 其中一個用於圖片生成(112x112分別率),可生成高質量的圖片。另一網路用於多類別任務,文章使用了中國字作為測試。
2. 傳統的GAN
GAN的學習過程即同時訓練Discriminator (D)和Generator (G)的過程,G從高斯分佈的變數, 學習潛在變數,來產生分佈,使得該分佈與真實分佈越接近越好。因此,G學習的是一個對映過程,通過變數對映空間來產生分佈。另一方方面,D是一個分類器,來判斷G產生的分佈是否與真實樣本接近,通過變數空間判斷是否一樣,同樣的也是一個對映。傳統GAN的代價函式如下:
(公式1)
這裡稍微解釋下:
- 整個式子由兩項構成。表示真實圖片,表示輸入網路的噪聲或者高斯分佈資料,而表示網路生成的圖片。
- 表示網路判斷真實圖片是否真實的概率(因為就是真實的,所以對於來說,這個值越接近1越好)。而是網路判斷生成的圖片的是否真實的概率。
- 的目的:是網路判斷生成的圖片是否真實的概率,應該希望自己生成的圖片“越接近真實越好”。也就是說,希望儘可能得大,這時會變小。因此我們看到式子的最前面的記號是。
- 的目的:的能力越強,應該越大,應該越小。這時會變大。因此式子對於來說是求最大(max_D)
3. Least Squares Generative Adversarial Networks
LSGANs在Discriminator上使用a-b編碼策略,簡單來說就是用a來代表“fake”資料,用b來代表“real”資料。LSGANs的目標函式為:
(公式2)
其中c代表生成器為了讓判斷器認為生成的資料是真實分佈資料而定的值。在文章中作者設定。
同時在文章中,作者列出了傳統的GAN其實在優化的是JS散度,具體參考Wasserstein GAN,
(公式3)
化為JS散度為
因此當倆個分佈沒有重疊或者重疊部分可忽略的時候,, 因此此時的梯度就變為0了。
因此,對於作者提出的LSGANs, 研究了LSGANs損失函式和f散度 (f-divergence)之間的聯絡:
