線段樹 詳解
線段樹詳解
By 巖之痕
目錄:
一:綜述
二:原理
三:遞迴實現
四:非遞迴原理
五:非遞迴實現
六:線段樹解題模型
七:掃描線
八:可持久化 (主席樹)
九:練習題
一:綜述
假設有編號從1到n的n個點,每個點都存了一些資訊,用[L,R]表示下標從L到R的這些點。
線段樹的用處就是,對編號連續的一些點進行修改或者統計操作,修改和統計的複雜度都是O(log2(n)).
線段樹的原理,就是,將[1,n]分解成若干特定的子區間(數量不超過4*n),然後,將每個區間[L,R]都分解為
少量特定的子區間,通過對這些少量子區間的修改或者統計,來實現快速對[L,R]的修改或者統計。
由此看出,用線段樹統計的東西,必須符合區間加法,否則,不可能通過分成的子區間來得到[L,R]的統計結果。
符合區間加法的例子:
數字之和——總數字之和 = 左區間數字之和 + 右區間數字之和
最大公因數(GCD)——總GCD = gcd( 左區間GCD , 右區間GCD );
最大值——總最大值=max(左區間最大值,右區間最大值)
不符合區間加法的例子:
眾數——只知道左右區間的眾數,沒法求總區間的眾數
01序列的最長連續零——只知道左右區間的最長連續零,沒法知道總的最長連續零
一個問題,只要能化成對一些連續點的修改和統計問題,基本就可以用線段樹來解決了,具體怎麼轉化在第六節會講。
由於點的資訊可以千變萬化,所以線段樹是一種非常靈活的資料結構,可以做的題的型別特別多,只要會轉化。
線段樹當然是可以維護線段資訊的,因為線段資訊也是可以轉換成用點來表達的(每個點代表一條線段)。
所以在以下對結構的討論中,都是對點的討論,線段和點的對應關係在第七節掃描線中會講。
本文二到五節是講對線段樹操作的原理和實現。
六到八節介紹了線段樹解題模型,以及一些例題。
初學者可以先看這篇文章: 線段樹從零開始
二:原理
(注:由於線段樹的每個節點代表一個區間,以下敘述中不區分節點和區間,只是根據語境需要,選擇合適的詞)
線段樹本質上是維護下標為1,2,..,n的n個按順序排列的數的資訊,所以,其實是“點樹”,是維護n的點的資訊,至於每個點的資料的含義可以有很多,
在對線段操作的線段樹中,每個點代表一條線段,在用線段樹維護數列資訊的時候,每個點代表一個數,但本質上都是每個點代表一個數。以下,在討論線段樹的時候,區間[L,R]指的是下標從L到R的這(R-L+1)個數,而不是指一條連續的線段。只是有時候這些數代表實際上一條線段的統計結果而已。
線段樹是將每個區間[L,R]分解成[L,M]和[M+1,R] (其中M=(L+R)/2 這裡的除法是整數除法,即對結果下取整)直到 L==R 為止。
開始時是區間[1,n] ,通過遞迴來逐步分解,假設根的高度為1的話,樹的最大高度為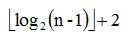
線段樹對於每個n的分解是唯一的,所以n相同的線段樹結構相同,這也是實現可持久化線段樹的基礎。
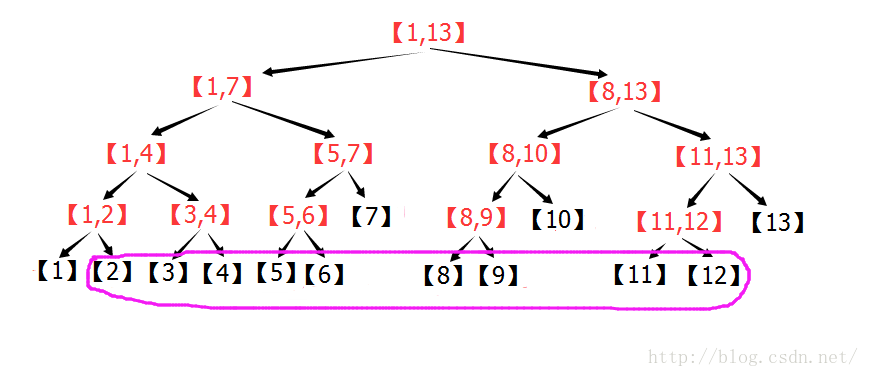
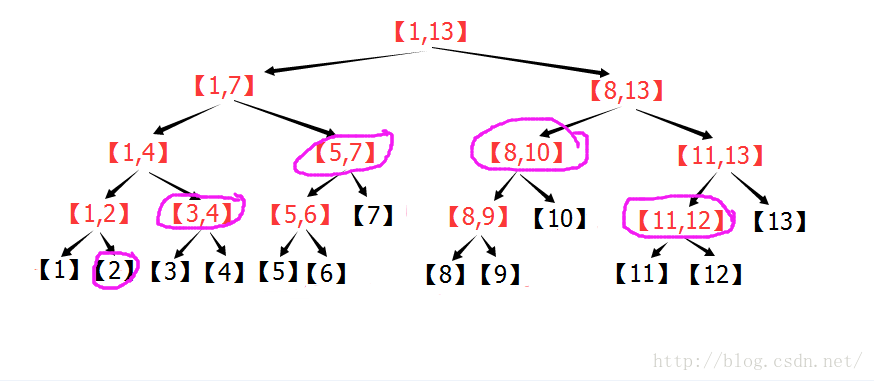
下圖展示了區間[1,13]的分解過程:
上圖中,每個區間都是一個節點,每個節點存自己對應的區間的統計資訊。
(1)線段樹的點修改:
假設要修改[5]的值,可以發現,每層只有一個節點包含[5],所以修改了[5]之後,只需要每層更新一個節點就可以線段樹每個節點的資訊都是正確的,所以修改次數的最大值為層數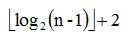
複雜度O(log2(n))
(2)線段樹的區間查詢:
線段樹能快速進行區間查詢的基礎是下面的定理:
定理:n>=3時,一個[1,n]的線段樹可以將[1,n]的任意子區間[L,R]分解為不超過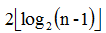
這樣,在查詢[L,R]的統計值的時候,只需要訪問不超過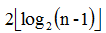
下面給出證明:
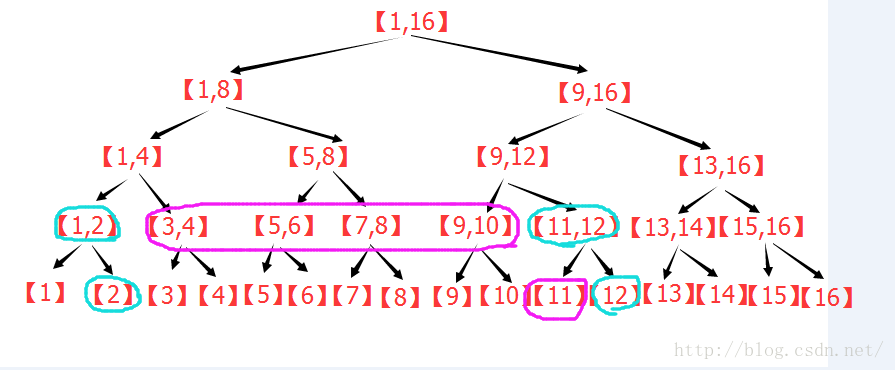
(2.1)先給出一個粗略的證明(結合下圖):
先考慮樹的最下層,將所有在區間[L,R]內的點選中,然後,若相鄰的點的直接父節點是同一個,那麼就用這個父節點代替這兩個節點(父節點在上一層)。這樣操作之後,本層最多剩下兩個節點。若最左側被選中的節點是它父節點的右子樹,那麼這個節點會被剩下。若最右側被選中的節點是它的父節點的左子樹,那麼這個節點會被剩下。中間的所有節點都被父節點取代。
對最下層處理完之後,考慮它的上一層,繼續進行同樣的處理,可以發現,每一層最多留下2個節點,其餘的節點升往上一層,這樣可以說明分割成的區間(節點)個數是大概是樹高的兩倍左右。
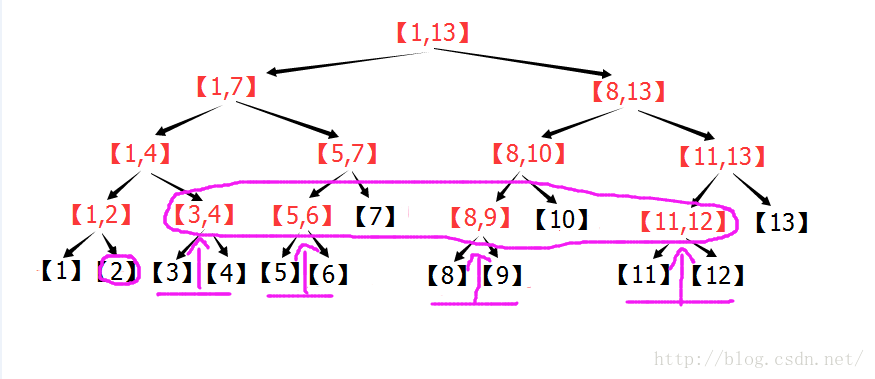
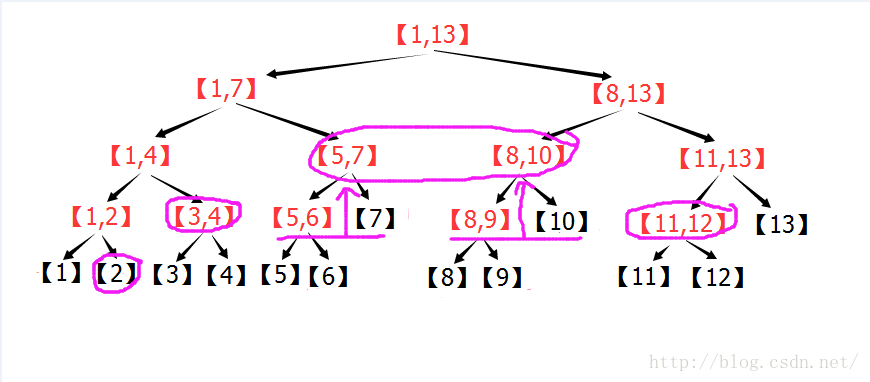
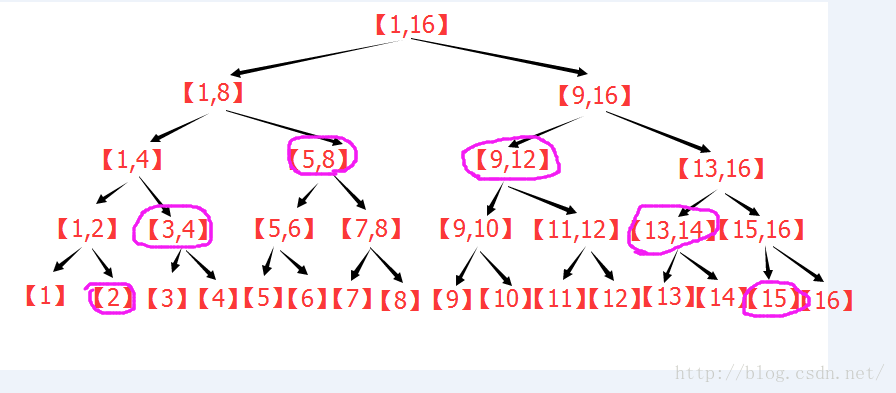
下圖為n=13的線段樹,區間[2,12],按照上面的敘述進行操作的過程圖:
由圖可以看出:在n=13的線段樹中,[2,12]=[2] + [3,4] + [5,7] + [8,10] + [11,12] 。
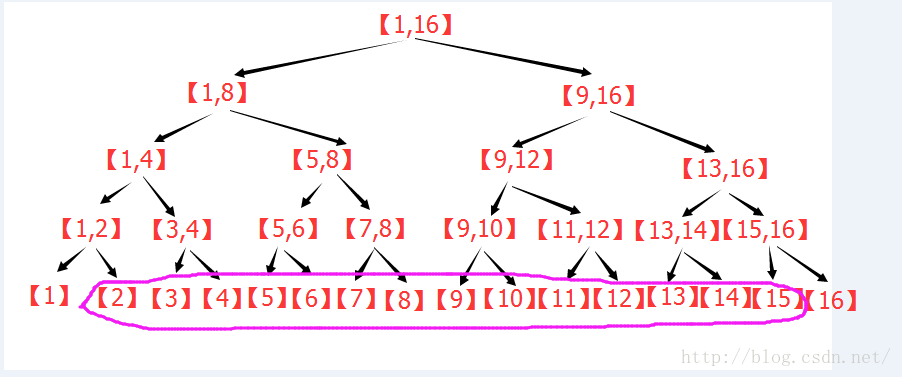
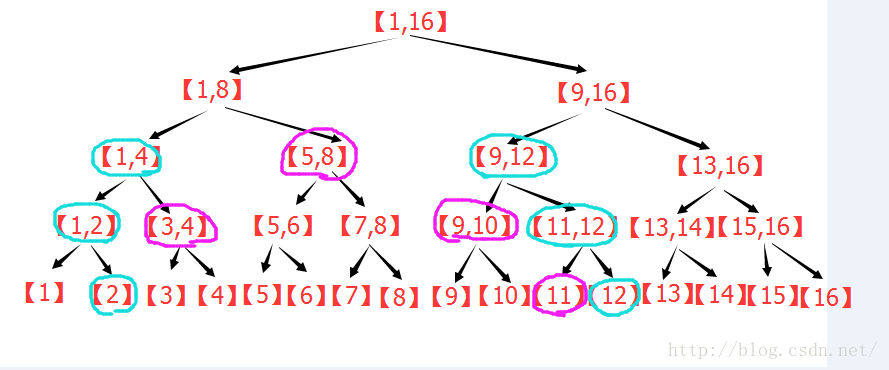
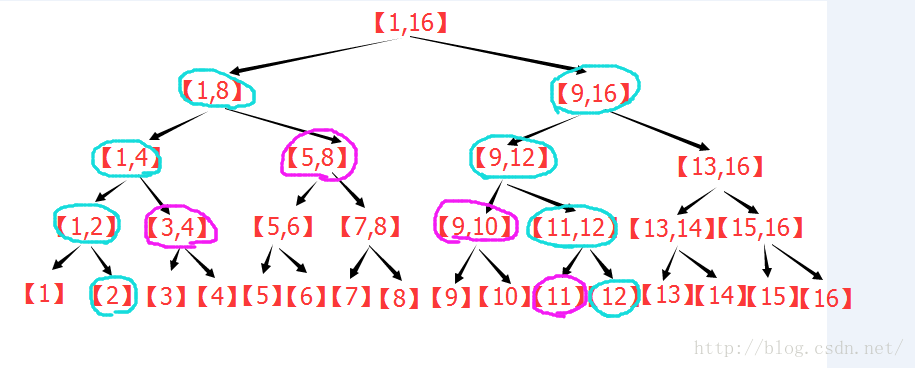
下圖是n=16 , L=2 , R=15 時的操作圖,此圖展示了達到最小上界的樹的結構。
(3)線段樹的區間修改:
線段樹的區間修改也是將區間分成子區間,但是要加一個標記,稱作懶惰標記。
標記的含義:
本節點的統計資訊已經根據標記更新過了,但是本節點的子節點仍需要進行更新。
即,如果要給一個區間的所有值都加上1,那麼,實際上並沒有給這個區間的所有值都加上1,而是打個標記,記下來,這個節點所包含的區間需要加1.打上標記後,要根據標記更新本節點的統計資訊,比如,如果本節點維護的是區間和,而本節點包含5個數,那麼,打上+1的標記之後,要給本節點維護的和+5。這是向下延遲修改,但是向上顯示的資訊是修改以後的資訊,所以查詢的時候可以得到正確的結果。有的標記之間會相互影響,所以比較簡單的做法是,每遞迴到一個區間,首先下推標記(若本節點有標記,就下推標記),然後再打上新的標記,這樣仍然每個區間操作的複雜度是O(log2(n))。
標記有相對標記和絕對標記之分:
相對標記是將區間的所有數+a之類的操作,標記之間可以共存,跟打標記的順序無關(跟順序無關才是重點)。
所以,可以在區間修改的時候不下推標記,留到查詢的時候再下推。
注意:如果區間修改時不下推標記,那麼PushUp函式中,必須考慮本節點的標記。
而如果所有操作都下推標記,那麼PushUp函式可以不考慮本節點的標記,因為本節點的標記一定已經被下推了(也就是對本節點無效了)
絕對標記是將區間的所有數變成a之類的操作,打標記的順序直接影響結果,
所以這種標記在區間修改的時候必須下推舊標記,不然會出錯。
注意,有多個標記的時候,標記下推的順序也很重要,錯誤的下推順序可能會導致錯誤。
之所以要區分兩種標記,是因為非遞迴線段樹只能維護相對標記。
因為非遞迴線段樹是自底向上直接修改分成的每個子區間,所以根本做不到在區間修改的時候下推標記。
非遞迴線段樹一般不下推標記,而是自下而上求答案的過程中,根據標記更新答案。
(4)線段樹的儲存結構:
線段樹是用陣列來模擬樹形結構,對於每一個節點R ,左子節點為 2*R (一般寫作R<<1)右子節點為 2*R+1(一般寫作R<<1|1)
然後以1為根節點,所以,整體的統計資訊是存在節點1中的。
這麼表示的原因看下圖就很明白了,左子樹的節點標號都是根節點的兩倍,右子樹的節點標號都是左子樹+1:
線段樹需要的陣列元素個數是: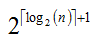
三:遞迴實現
以下以維護數列區間和的線段樹為例,演示最基本的線段樹程式碼。
(0)定義:
- #define maxn 100007 //元素總個數
- #define ls l,m,rt<<1
- #define rs m+1,r,rt<<1|1
- int Sum[maxn<<2],Add[maxn<<2];//Sum求和,Add為懶惰標記
- int A[maxn],n;//存原陣列資料下標[1,n]
(1)建樹:
- //PushUp函式更新節點資訊 ,這裡是求和
- void PushUp(int rt){Sum[rt]=Sum[rt<<1]+Sum[rt<<1|1];}
- //Build函式建樹
- void Build(int l,int r,int rt){ //l,r表示當前節點區間,rt表示當前節點編號
- if(l==r) {//若到達葉節點
- Sum[rt]=A[l];//儲存陣列值
- return;
- }
- int m=(l+r)>>1;
- //左右遞迴
- Build(l,m,rt<<1);
- Build(m+1,r,rt<<1|1);
- //更新資訊
- PushUp(rt);
- }
(2)點修改:
假設A[L]+=C:
- void Update(int L,int C,int l,int r,int rt){//l,r表示當前節點區間,rt表示當前節點編號
- if(l==r){//到葉節點,修改
- Sum[rt]+=C;
- return;
- }
- int m=(l+r)>>1;
- //根據條件判斷往左子樹呼叫還是往右
- if(L <= m) Update(L,C,l,m,rt<<1);
- else Update(L,C,m+1,r,rt<<1|1);
- PushUp(rt);//子節點更新了,所以本節點也需要更新資訊
- }
(3)區間修改:
假設A[L,R]+=C
- void Update(int L,int R,int C,int l,int r,int rt){//L,R表示操作區間,l,r表示當前節點區間,rt表示當前節點編號
- if(L <= l && r <= R){//如果本區間完全在操作區間[L,R]以內
- Sum[rt]+=C*(r-l+1);//更新數字和,向上保持正確
- Add[rt]+=C;//增加Add標記,表示本區間的Sum正確,子區間的Sum仍需要根據Add的值來調整
- return ;
- }
- int m=(l+r)>>1;
- PushDown(rt,m-l+1,r-m);//下推標記
- //這裡判斷左右子樹跟[L,R]有無交集,有交集才遞迴
- if(L <= m) Update(L,R,C,l,m,rt<<1);
- if(R > m) Update(L,R,C,m+1,r,rt<<1|1);
- PushUp(rt);//更新本節點資訊
- }
(4)區間查詢:
詢問A[L,R]的和
首先是下推標記的函式:
- void PushDown(int rt,int ln,int rn){
- //ln,rn為左子樹,右子樹的數字數量。
- if(Add[rt]){
- //下推標記
- Add[rt<<1]+=Add[rt];
- Add[rt<<1|1]+=Add[rt];
- //修改子節點的Sum使之與對應的Add相對應
- Sum[rt<<1]+=Add[rt]*ln;
- Sum[rt<<1|1]+=Add[rt]*rn;
- //清除本節點標記
- Add[rt]=0;
- }
- }
然後是區間查詢的函式:
- int Query(int L,int R,int l,int r,int rt){//L,R表示操作區間,l,r表示當前節點區間,rt表示當前節點編號
- if(L <= l && r <= R){
- //在區間內,直接返回
- return Sum[rt];
- }
- int m=(l+r)>>1;
- //下推標記,否則Sum可能不正確
- PushDown(rt,m-l+1,r-m);
- //累計答案
- int ANS=0;
- if(L <= m) ANS+=Query(L,R,l,m,rt<<1);
- if(R > m) ANS+=Query(L,R,m+1,r,rt<<1|1);
- return ANS;
- }
(5)函式呼叫:
- //建樹
- Build(1,n,1);
- //點修改
- Update(L,C,1,n,1);
- //區間修改
- Update(L,R,C,1,n,1);
- //區間查詢
- int ANS=Query(L,R,1,n,1);
感謝幾位網友指出了我的錯誤。
我說相對標記在Update時可以不下推,這一點是對的,但是原來的程式碼是錯誤的。
因為原來的程式碼中,PushUP函式是沒有考慮本節點的Add值的,如果Update時下推標記,那麼PushUp的時候,節點的Add值一定為零,所以不需要考慮Add。
但是,如果Update時暫時不下推標記的話,那麼PushUp函式就必須考慮本節點的Add值,否則會導致錯誤。
為了簡便,上面函式中,PushUp函式沒有考慮Add標記。所以無論是相對標記還是絕對標記,在更新資訊的時候,
到達的每個節點都必須呼叫PushDown函式來下推標記,另外,程式碼中,點修改函式中沒有PushDown函式,因為這裡假設只有點修改一種操作,
如果題目中是點修改和區間修改混合的話,那麼點修改中也需要PushDown。
四:非遞迴原理
非遞迴的思路很巧妙,思路以及部分程式碼實現 來自 清華大學 張昆瑋 《統計的力量》 ,有興趣可以去找來看。
非遞迴的實現,程式碼簡單(尤其是點修改和區間查詢),速度快,建樹簡單,遍歷元素簡單。總之能非遞迴就非遞迴吧。
不過,要支援區間修改的話,程式碼會變得複雜,所以區間修改的時候還是要取捨。有個特例,如果區間修改,但是隻需要
在所有操作結束之後,一次性下推所有標記,然後求結果,這樣的話,非遞迴寫起來也是很方便的。
下面先講思路,再講實現。
點修改:
非遞迴的思想總的來說就是自底向上進行各種操作。回憶遞迴線段樹的點修改,首先由根節點1向下遞迴,找到對應的葉
節點,然後,修改葉節點的值,再向上返回,在函式返回的過程中,更新路徑上的節點的統計資訊。而非遞迴線段樹的思路是,
如果可以直接找到葉節點,那麼就可以直接從葉節點向上更新,而一個節點找父節點是很容易的,編號除以2再下取整就行了。
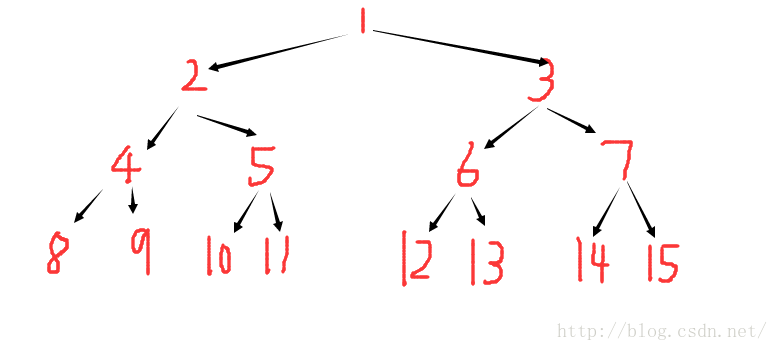
那麼,如何可以直接找到葉節點呢?非遞迴線段樹擴充了普通線段樹(假設元素數量為n),使得所有非葉結點都有兩個子結點且葉子結點都在同一層。
來觀察一下擴充後的性質:
可以注意到紅色和黑色數字的差是固定的,如果事先算出這個差值,就可以直接找到葉節點。
注意:區分3個概念:原陣列下標,線段樹中的下標和儲存下標。
原陣列下標,是指,需要維護統計資訊(比如區間求和)的陣列的下標,這裡都預設下標從1開始(一般用A陣列表示)
線段樹下標,是指,加入線段樹中某個位置的下標,比如,原陣列中的第一個數,一般會加入到線段樹中的第二個位置,
為什麼要這麼做,後面會講。
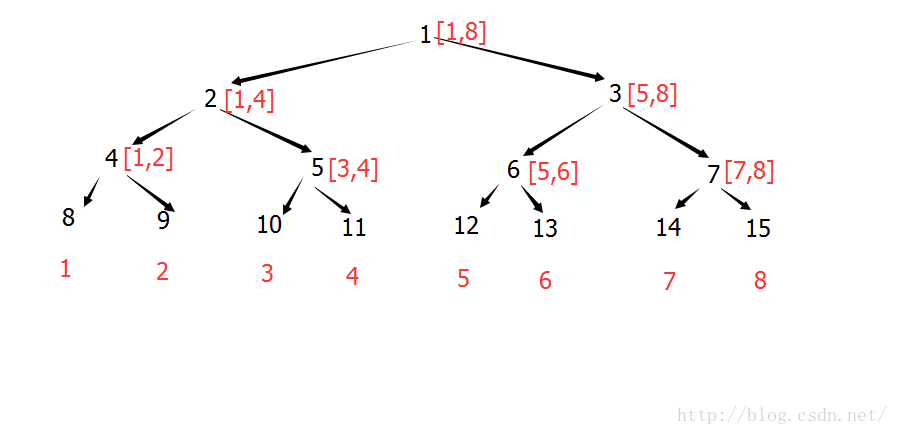
儲存下標,是指該元素所在的葉節點的編號,即實際儲存的位置。
【在上面的圖片中,紅色為原陣列下標,黑色為儲存下標】
有了這3個概念,下面開始講區間查詢。
點修改下的區間查詢:
首先,區間的劃分沒有變,現在關鍵是如何直接找到被分成的區間。原來是遞迴查詢,判斷左右子區間跟[L,R]是否有交點,
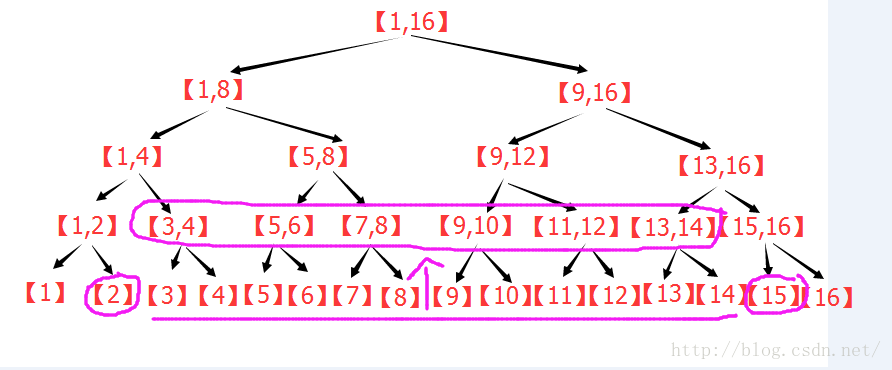
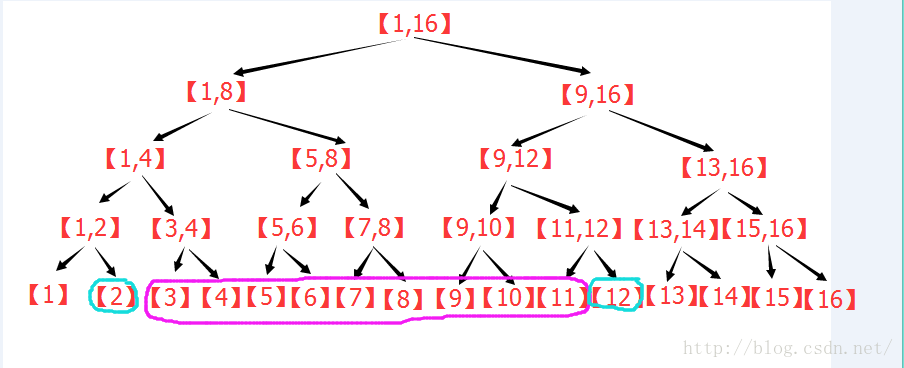
若有交點則向下遞迴。現在要非遞迴實現,這就是巧妙之處,見下圖,以查詢[3,11]為例子。
其實,容易發現,紫色部分的變化,跟原來分析線段樹的區間分解的時候是一樣的規則,圖中多的藍色是什麼意思呢?
首先注意到,藍色節點剛好在紫色節點的兩端。
回憶一下,原來線段樹在區間逐層被替代的過程中,哪些節點被留了下來?最左側的節點,若為其父節點的右子節點,則留下。
最右側的節點,若為其父節點的左子節點則留下。那麼對於包裹著紫色的藍色節點來看,剛好相反。
比如,以左側的的藍色為例,若該節點是其父節點的右子節點,就證明它右側的那個紫色節點不會留下,會被其父替代,所以沒必要在這一步計算,若該節點是其父節點的左子節點,就證明它右側的那個紫色節點會留在這一層,所以必須在此刻計算,否則以後都不會再計算這個節點了。這樣逐層上去,容易發現,對於左側的藍色節點來說,只要它是左子節點,那麼就要計算對應的右子節點。同理,對於右側的藍色節點,只要它是右子節點,就需要計算它對應的左子節點。這個計算一直持續到左右藍色節點的父親為同一個的時候,才停止。於是,區間查詢,其實就是兩個藍色節點一路向上走,在路徑上更新答案。這樣,區間修改就變成了兩條同時向根走的鏈,明顯複雜度O(log2(n))。並且可以非遞迴實現。
至此,區間查詢也解決了,可以直接找到所有分解成的區間。
但是有一個問題,如果要查詢[1,5]怎麼辦?[1]左邊可是沒地方可以放置藍色節點了。
問題的解決辦法簡單粗暴,原陣列的1到n就不存線上段樹的1到n了,而是存線上段樹的2到n+1,
而開始要建立一顆有n+2個元素的樹,空出第一個和最後一個元素的空間。
現在來講如何對線段樹進行擴充。
再來看這個二叉樹,令N=8;注意到,該樹可以存8個元素,並且[1..7]是非葉節點,[8..15]是葉節點。
也就是說,左下角為N的二叉樹,可以存N個元素,並且[1..N-1]是非葉節點,[N..2N-1]是葉節點。
並且,線段樹下標+N-1=儲存下標 (還記不記得原來對三個下標的定義)
這時,這個線段樹存在兩段座標對映:
原陣列下標+1=線段樹下標
線段樹下標+N-1=儲存下標
聯立方程得到:原陣列下標+N=儲存下標
於是從原陣列下標到儲存下標的轉換及其簡單。
下一個問題:N怎麼確定?
上面提到了,N的含義之一是,這棵樹可以存N個元素,也就是說N必須大於等於n+2
於是,N的定義,N是大於等於n+2的,某個2的次方。
區間修改下的區間查詢:
方法之一:如果題目許可,可以直接打上標記,最後一次下推所有標記,然後就可以遍歷葉節點來獲取資訊。
方法之二:如果題目查詢跟修改混在一起,那麼,採用標記永久化思想。也就是,不下推標記。
遞迴線段樹是在查詢區間的時候下推標記,使得到達每個子區間的時候,Sum已經是正確值。
非遞迴沒法這麼做,非遞迴是從下往上,遇到標記就更新答案。
這題是Add標記,一個區間Add標記表示這個區間所有元素都需要增加Add
Add含義不變,Add仍然表示本節點的Sum已經更新完畢,但是子節點的Sum仍需要更新.
現在就是如何在查詢的時候根據標記更新答案。
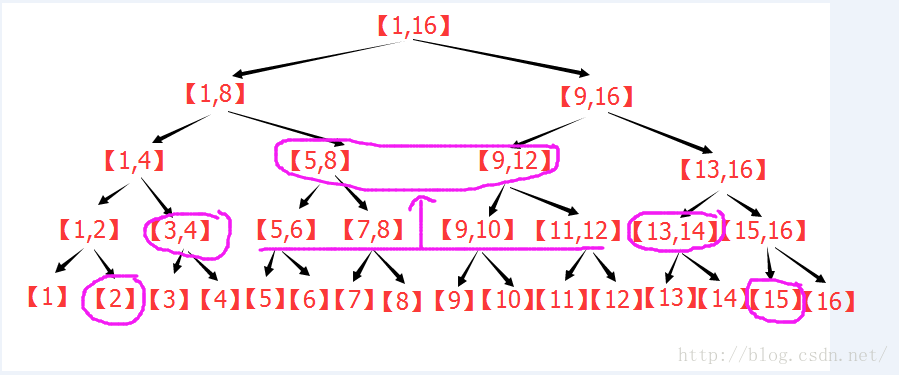
觀察下圖:
左邊的藍色節點從下往上走,在藍色節點到達[1,4]時,注意到,左邊藍色節點之前計算過的所有節點(即[3,4])都是目前藍色節點的子節點也就是說,當前藍色節點的Add是要影響這個節點已經計算過的所有數。多用一個變數來記錄這個藍色節點已經計算過多少個數,根據個數以及當前藍色節點的Add,來更新最終答案。
更新完答案之後,再加上[5,8]的答案,同時當前藍色節點計算過的個數要+4(因為[5,8]裡有4個數)
然後當這個節點到達[1,8]節點時,可以更新[1,8]的Add.
這裡,本來左右藍色節點相遇之後就不再需要計算了,但是由於有了Add標記,左右藍色節點的公共祖先上的Add標記會影響目前的所有數,所以還需要一路向上查詢到根,沿路根據Add更新答案。
區間修改:
這裡講完了查詢,再來講講修改,
修改的時候,給某個區間的Add加上了C,這個區間的子區間向上查詢時,會經過這個節點,也就是會計算這個Add,但是
如果路徑經過這個區間的父節點,就不會計算這個節點的Add,也就會出錯。這裡其實跟遞迴線段樹一樣,改了某個區間的Add
仍需要向上更新所有包含這個區間的Sum,來保持上面所有節點的正確性。
五:非遞迴實現
以下以維護數列區間和的線段樹為例,演示最基本的非遞迴線段樹程式碼。
(0)定義:
- //
- #define maxn 100007
- int A[maxn],n,N;//原陣列,n為原陣列元素個數 ,N為擴充元素個數
- int Sum[maxn<<2];//區間和
- int Add[maxn<<2];//懶惰標記
(1)建樹:
- //
- void Build(int n){
- //計算N的值
- N=1;while(N < n+2) N <<= 1;
- //更新葉節點
- for(int i=1;i<=n;++i) Sum[N+i]=A[i];//原陣列下標+N=儲存下標
- //更新非葉節點
- for(int i=N-1;i>0;--i){
- //更新所有非葉節點的統計資訊
- Sum[i]=Sum[i<<1]+Sum[i<<1|1];
- //清空所有非葉節點的Add標記
- Add[i]=0;
- }
- }
(2)點修改:
A[L]+=C
- //
- void Update(int L,int C){
- for(int s=N+L;s;s>>=1){
- Sum[s]+=C;
- }
- }
(3)點修改下的區間查詢:
求A[L..R]的和(點修改沒有使用Add所以不需要考慮)
程式碼非常簡潔,也不難理解,
s和t分別代表之前的論述中的左右藍色節點,其餘的程式碼根據之前的論述應該很容易看懂了。
s^t^1 在s和t的父親相同時值為0,終止迴圈。
兩個if是判斷s和t分別是左子節點還是右子節點,根據需要來計算Sum
- //
- int Query(int L,int R){
- int ANS=0;
- for(int s=N+L-1,t=N+R+1;s^t^1;s>>=1,t>>=1){
- if(~s&1) ANS+=Sum[s^1];
- if( t&1) ANS+=Sum[t^1];
- }
- return ANS;
- }
(4)區間修改:
A[L..R]+=C
- <span style="font-size:14px;">//
- void Update(int L,int R,int C){
- int s,t,Ln=0,Rn=0,x=1;
- //Ln: s一路走來已經包含了幾個數
- //Rn: t一路走來已經包含了幾個數
- //x: 本層每個節點包含幾個數
- for(s=N+L-1,t=N+R+1;s^t^1;s>>=1,t>>=1,x<<=1){
- //更新Sum
- Sum[s]+=C*Ln;
- Sum[t]+=C*Rn;
- //處理Add
- if(~s&1) Add[s^1]+=C,Sum[s^1]+=C*x,Ln+=x;
- if( t&1) Add[t^1]+=C,Sum[t^1]+=C*x,Rn+=x;
- }
- //更新上層Sum
- for(;s;s>>=1,t>>=1){
- Sum[s]+=C*Ln;
- Sum[t]+=C*Rn;
- }
- } </span>
(5)區間修改下的區間查詢:
求A[L..R]的和
- //
- int Query(int L,int R){
- int s,t,Ln=0,Rn=0,x=1;
- int ANS=0;
- for(s=N+L-1,t=N+R+1;s^t^1;s>>=1,t>>=1,x<<=1){
- //根據標記更新
- if(Add[s]) ANS+=Add[s]*Ln;
- if(Add[t]) ANS+=Add[t]*Rn;
- //常規求和
- if(~s&1) ANS+=Sum[s^1],Ln+=x;
- if( t&1) ANS+=Sum[t^1],Rn+=x;
- }
- //處理上層標記
- for(;s;s>>=1,t>>=1){
- ANS+=Add[s]*Ln;
- ANS+=Add[t]*Rn;
- }
- return ANS;
- }
六:線段樹解題模型
給出線段樹解題模型以及一些例題。
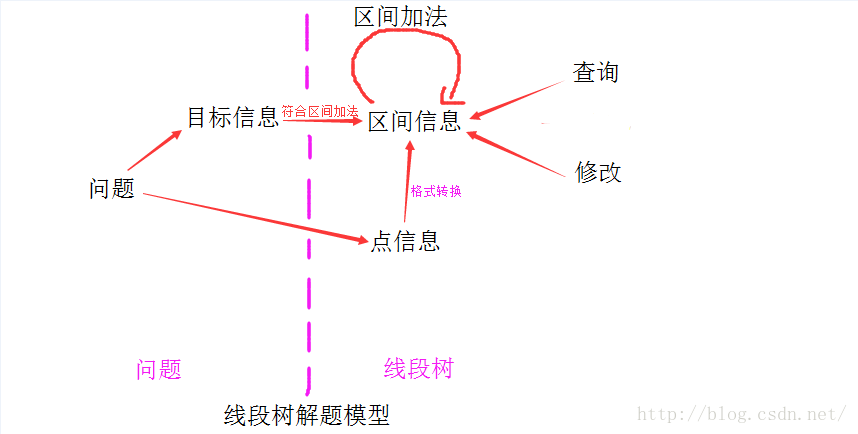
先對圖中各個名字給出定義:
問題:可能可以用線段樹解決的問題
目標資訊:由問題轉換而成的,為了解決問題而需要統計的資訊(可能不滿足區間加法)。
點資訊:每個點儲存的資訊
區間資訊:每個區間維護的資訊(線段樹節點定義) (必須滿足區間加法)
區間資訊包括 統計資訊和標記
--------統計資訊:統計節點代表的區間的資訊,一般自下而上更新
--------標記:對操作進行標記(在區間修改時需要),一般自上而下傳遞,或者不傳遞
區間加法:實現區間加法的程式碼
查詢:實現查詢操作的程式碼
修改:實現修改操作的程式碼
圖中紫線右邊是實際線段樹的實現,左邊是對問題的分析以及轉換。
一個問題,若能轉換成對一些連續點的修改或者統計,就可以考慮用線段樹解決。
首先確定目標資訊和點資訊,然後將目標資訊轉換成區間資訊(必要時,增加資訊,使之符合區間加法)。
之後就是線段樹的程式碼實現了,包括:
1.區間加法
2.建樹,點資訊到區間資訊的轉換
3.每種操作(包括查詢,修改)對區間資訊的呼叫,修改
這樣,點的資訊不同,區間資訊不同,線段樹可以維護很多種類的資訊,所以是一種非常實用的資料結構。
可以解決很多問題,下面給出幾個例子來說明。
(1):字串雜湊
題目:URAL1989 Subpalindromes 題解
給定一個字串(長度<=100000),有兩個操作。 1:改變某個字元。 2:判斷某個子串是否構成迴文串。
直接判斷會超時。這個題目,是用線段樹維護字串雜湊
對於一個字串a[0],a[1],...,a[n-1] 它對應的雜湊函式為a[0]+a[1]*K + a[2]*K^2 +...+a[n-1]*K^(n-1)
再維護一個從右往左的雜湊值:a[0]*K^(n-1) + a[1]*K^(n-2) +...+a[n-1]
若是迴文串,則左右的雜湊值會相等。而左右雜湊值相等,則很大可能這是迴文串。
若出現誤判,可以再用一個K2,進行二次雜湊判斷,可以減小誤判概率。
實現上,雜湊值最好對某個質數取餘數,這樣分佈更均勻。
解題模型:
問題經過轉換之後:
目標資訊:某個區間的左,右雜湊值
點資訊:一個字元
目標資訊已經符合區間加法,所以區間資訊=目標資訊。
所以線段樹的結構為:
區間資訊:區間雜湊值
點資訊:一個字元
程式碼主要需要注意2個部分:
1.區間加法 :(PushUp函式,Pow[a]=K^a)
2.點資訊->區間資訊:(葉節點上,區間只包含一個點,所以需要將點資訊轉換成區間資訊)
修改以及查詢,在有了區間加法的情況下,沒什麼難度了。
可以看出,上述解題過程的核心,就是找到區間資訊, 寫好區間加法。
下面是維護區間和的部分,下面的程式碼沒有取餘,也就是實際上是對2^32取餘數,這樣其實分佈不均勻,容易出現誤判:
- //
- #define K 137
- #define maxn 100001
- char str[maxn];
- int Pow[maxn];//K的各個次方
- struct Node{
- int KeyL,KeyR;
- Node():KeyL(0),KeyR(0){}
- void init(){KeyL=KeyR=0;}
- }node[maxn<<2];
- void PushUp(int L,int R,int rt){
- node[rt].KeyL=node[rt<<1].KeyL+node[rt<<1|1].KeyL*Pow[L];
- node[rt].KeyR=node[rt<<1].KeyR*Pow[R]+node[rt<<1|1].KeyR;
- }
(2):最長連續零
題目:Codeforces 527C Glass Carving 題解
題意是給定一個矩形,不停地縱向或橫向切割,問每次切割後,最大的矩形面積是多少。
最大矩形面積=最長的長*最寬的寬
這題,長寬都是10^5,所以,用01序列表示每個點是否被切割,然後,
最長的長就是長的最長連續0的數量+1
最長的寬就是寬的最長連續0的數量+1
於是用線段樹維護最長連續零
問題轉換成:
目標資訊:區間最長連續零的個數
點資訊:0 或 1
由於目標資訊不符合區間加法,所以要擴充目標資訊。
轉換後的線段樹結構:
區間資訊:從左,右開始的最長連續零,本區間是否全零,本區間最長連續零。
點資訊:0 或 1
然後還是那2個問題:
1.區間加法:
這裡,一個區間的最長連續零,需要考慮3部分:
-(1):左子區間最長連續零
-(2):右子區間最長連續零
-(3):左右子區間拼起來,而在中間生成的連續零(可能長於兩個子區間的最長連續零)
而中間拼起來的部分長度,其實是左區間從右開始的最長連續零+右區間從左開始的最長連續零。
所以每個節點需要多兩個量,來存從左右開始的最長連續零。
然而,左開始的最長連續零分兩種情況,
--(1):左區間不是全零,那麼等於左區間的左最長連續零
--(2):左區間全零,那麼等於左區間0的個數加上右區間的左最長連續零
於是,需要知道左區間是否全零,於是再多加一個變數。
最終,通過維護4個值,達到了維護區間最長連續零的效果。
2.點資訊->區間資訊 :
如果是0,那麼 最長連續零=左最長連續零=右最長連續零=1 ,全零=true。
如果是1,那麼 最長連續零=左最長連續零=右最長連續零=0, 全零=false。
至於修改和查詢,有了區間加法之後,機械地寫一下就好了。
由於這裡其實只有對整個區間的查詢,所以查詢函式是不用寫的,直接找根的統計資訊就行了。
程式碼如下:
- //
- #define maxn 200001
- using namespace std;
- int L[maxn<<2][2];//從左開始連續零個數
- int R[maxn<<2][2];//從右
- int Max[maxn<<2][2];//區間最大連續零
- bool Pure[maxn<<2][2];//是否全零
- int M[2];
- void PushUp(int rt,int k){//更新rt節點的四個資料 k來選擇兩棵線段樹
- Pure[rt][k]=Pure[rt<<1][k]&&Pure[rt<<1|1][k];
- Max[rt][k]=max(R[rt<<1][k]+L[rt<<1|1][k],max(Max[rt<<1][k],Max[rt<<1|1][k]));
- L[rt][k]=Pure[rt<<1][k]?L[rt<<1][k]+L[rt<<1|1][k]:L[rt<<1][k];
- R[rt][k]=Pure[rt<<1|1][k]?R[rt<<1|1][k]+R[rt<<1][k]:R[rt<<1|1][k];
- }
(3):計數排序
題目:Codeforces 558E A Simple Task 題解
給定一個長度不超過10^5的字串(小寫英文字母),和不超過5000個操作。
每個操作 L R K 表示給區間[L,R]的字串排序,K=1為升序,K=0為降序。
最後輸出最終的字串。
題目轉換成:
目標資訊:區間的計數排序結果
點資訊:一個字元
這裡,目標資訊是符合區間加法的,但是為了支援區間操作,還是需要擴充資訊。
轉換後的線段樹結構:
區間資訊:區間的計數排序結果,排序標記,排序種類(升,降)
點資訊:一個字元
程式碼中需要解決的四個問題(難點在於標記下推和區間修改):
1.區間加法
對應的字元數量相加即可(注意標記是不上傳的,所以區間加法不考慮標記)。
2.點資訊->區間資訊:把對應字元的數量設定成1,其餘為0,排序標記為false。
3.標記下推
明顯,排序標記是絕對標記,也就是說,標記對子節點是覆蓋式的效果,一旦被打上標記,下層節點的一切資訊都無效。
下推標記時,根據自己的排序結果,將元素分成對應的部分,分別裝入兩個子樹。
4.區間修改
這個是難點,由於要對某個區間進行排序,首先對各個子區間求和(求和之前一定要下推標記,才能保證求的和是正確的)
由於使用的計數排序,所以求和之後,新順序也就出來了。然後按照排序的順序按照每個子區間的大小來分配字元。
操作後,每個子區間都被打上了標記。
最後,在所有操作結束之後,一次下推所有標記,就可以得到最終的字元序列。
這裡只給出節點定義。
- //
- struct Node{
- int d[26];//計數排序
- int D;//總數
- bool sorted;//是否排好序
- bool Inc;//是否升序
- };
(4)總結:
總結一下,線段樹解題步驟。
一:將問題轉換成點資訊和目標資訊。
即,將問題轉換成對一些點的資訊的統計問題。
二:將目標資訊根據需要擴充成區間資訊
1.增加資訊符合區間加法。
2.增加標記支援區間操作。
三:程式碼中的主要模組:
1.區間加法
2.標記下推
3.點資訊->區間資訊
4.操作(各種操作,包括修改和查詢)
完成第一步之後,題目有了可以用線段樹解決的可能。
完成第二步之後,題目可以由線段樹解決。
第三步就是慢慢寫程式碼了。
七:掃描線
線段樹的一大應用是掃描線。
先把相關題目給出,有興趣可以去找來練習:
POJ 1177 Picture:給定若干矩形求合併之後的圖形周長 題解
HDU 1255 覆蓋的面積:給定平面上若干矩形,求出被這些矩形覆蓋過至少兩次的區域的面積. 題解
HDU 3642 Get The Treasury:給定若干空間立方體,求重疊了3次或以上的體積(這個是掃描面,每個面再掃描線)題解
再補充一道稍微需要一點模型轉換的掃描線題:
POJ 2482 Stars in your window : 給定一些星星的位置和亮度,求用W*H的矩形能夠框住的星星亮度之和最大為多少。
這題是把星星轉換成了矩形,把矩形框轉換成了點,然後再掃描線。 題解
掃描線求重疊矩形面積:
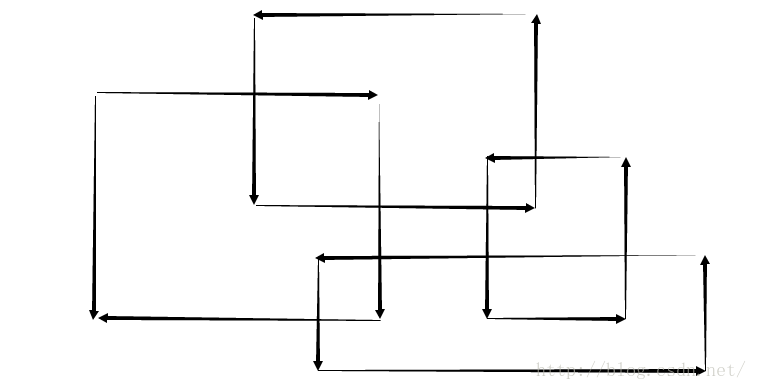
考慮下圖中的四個矩形:
觀察第三個圖:
掃描線的思路:使用一條垂直於X軸的直線,從左到右來掃描這個圖形,明顯,只有在碰到矩形的左邊界或者右邊界的時候,
這個線段所掃描到的情況才會改變,所以把所有矩形的入邊,出邊按X值排序。然後根據X值從小到大去處理,就可以
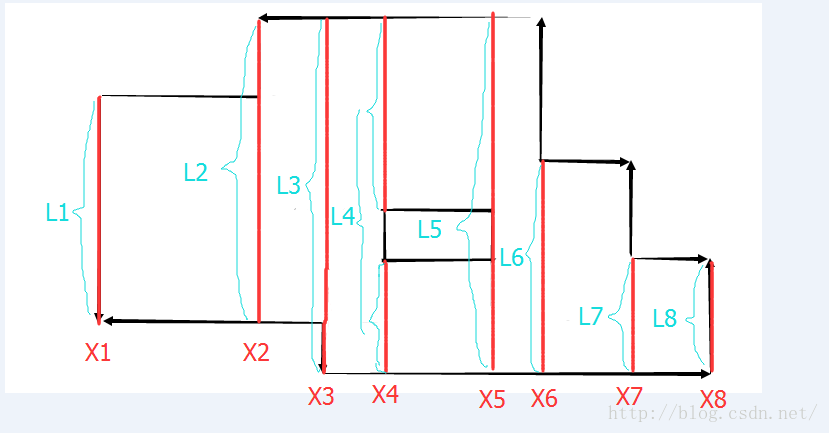
用線段樹來維護掃描到的情況。如上圖,X1到X8是所有矩形的入邊,出邊的X座標。
而紅色部分的線段,是這樣,如果碰到矩形的入邊,就把這條邊加入,如果碰到出邊,就拿走。紅色部分就是有線段覆蓋的部分。
要求面積,只需要知道圖中的L1到L8。而線段樹就是用來維護這個L1到L8的。
掃描線演算法流程:
X1:首先遇到X1,將第一條線段加入線段樹,由線段樹統計得到線段長度為L1.
X2:然後繼續掃描到X2,此時要進行兩個動作:
1.計算面積,目前掃過的面積=L1*(X2-X1)
2.更新線段。由於X2處仍然是入邊,所以往線段樹中又加了一條線段,加的這條線段可以參考3幅圖中的第一幅。
然後線段樹自動得出此時覆蓋的線段長度為L2 (注意兩條線段有重疊部分,重疊部分的長度只能算一次)
X3:繼續掃描到X3,步驟同X2
先計算 掃過的面積+=L2*(X3-X2)
再加入線段,得到L3.
X4:掃描到X4有些不一樣了。
首先還是計算 掃過的面積+=L3*(X4-X3)
然後這時遇到了第一個矩形的出邊,這時要從線段樹中刪除一條線段。
刪除之後的結果是線段樹中出現了2條線段,線段樹自動維護這兩條線段的長度之和L4
講到這裡演算法流程應該很清晰了。
首先將所有矩形的入邊,出邊都存起來,然後根據X值排序。
這裡用一個結構體,來存這些資訊,然後排序。
- //
- struct LINE{
- int x;//橫座標
- int y1,y2;//矩形縱向線段的左右端點
- bool In;//標記是入邊還是出邊
- bool operator < (const Line &B)const{return x < B.x;}
- }Line[maxn];
然後掃描的時候,需要兩個變數,一個叫PreL,存前一個x的操作結束之後的L值,和X,前一個橫座標。
假設一共有Ln條線段,線段下標從0開始,已經排好序。
那麼演算法大概是這樣:
- //
- int PreL=0;//前一個L值,剛開始是0,所以第一次計算時不會引入誤差
- int X;//X值
- int ANS=0;//存累計面積
- int I=0;//線段的下標
- while(I < Ln){
- //先計算面積
- ANS+=PreL*(Line[I].x-X);
- X=Line[I].x;//更新X值
- //對所有X相同的線段進行操作
- while(I < Ln && Line[I].x == X){
- //根據入邊還是出邊來選擇加入線段還是移除線段
- if(Line[I].In) Cover(Line[I].y1,Line[I].y2-1,1,n,1);
- else Uncover(Line[I].y1,Line[I].y2-1,1,n,1);
- ++I;
- }
- }
無論是求面積還是周長,掃描線的結構大概就是上面的樣子。
需要解決的幾個問題:
現在有兩點需要說明一下。
(1):線段樹進行線段操作時,每個點的含義(比如為什麼Cover函式中,y2後面要-1)。
(2):線段樹如何維護掃描線過程中的覆蓋線段長度。
(3):線段樹如何維護掃描線過程中線段的數量。
(1):線段樹中點的含義
線段樹如果沒有離散化,那麼線段樹下標為1,就代表線段[1,2)
線段樹下標為K的時候,代表的線段為[K,K+1) (長度為1)
所以,將上面的所有線段都化為[y1,y2)就可以理解了,線段[y1,y2)只包括線段樹下標中的y1,y1+1,...,y2-1
當y值的範圍是10^9時,就不能再按照上面的辦法按值建樹了,這時需要離散化。
下面是離散化的程式碼:
- //
- int Rank[maxn],Rn;
- void SetRank(){//呼叫前,所有y值被無序存入Rank陣列,下標為[1..Rn]
- int I=1;
- //第一步排序
- sort(Rank+1,Rank+1+Rn);
- //第二步去除重複值
- for(int i=2;i<=Rn;++i) if(Rank[i]!=Rank[i-1]) Rank[++I]=Rank[i];
- Rn=I;
- //此時,所有y值被從小到大無重複地存入Rank陣列,下標為[1..Rn]
- }
- int GetRank(int x){//給定x,求x的下標
- //二分法求下標
- int L=1,R=Rn,M;//[L,R] first >=x
- while(L!=R){
- M=(L+R)>>1;
- if(Rank[M]<x) L=M+1;
- else R=M;
- }
- return L;
- }
此時,線段樹的下標的含義就變成:如果線段樹下標為K,代表線段[ Rank[K] , Rank[K+1] )。
下標為K的線段長度為Rank[K+1]-Rank[K]
所以此時葉節點的線段長度不是1了。
這時,之前的掃描線演算法的函式呼叫部分就稍微的改變了一點:
- //
- if(Line[I].In) Cover(GetRank(Line[I].y1),GetRank(Line[I].y2)-1,1,n,1);
- else Uncover(GetRank(Line[I].y1),GetRank(Line[I].y2)-1,1,n,1);
看著有點長,其實不難理解,只是多了一步從y值到離散之後的下標的轉換。
注意一點,如果下標為K的線段長度為Rank[K+1]-Rank[K],那麼下標為Rn的線段樹的長度呢?
其實這個不用擔心,Rank[Rn]作為所有y值中的最大值,它肯定是一個線段的右端點,
而右端點求完離散之後的下標還要-1,所以上面的線段覆蓋永遠不會覆蓋到Rn。
所以線段樹其實只需要建立Rn-1個元素,因為下標為Rn的無法定義,也不會被訪問。
不過有時候留著也有好處,這個看具體實現時自己取捨。
(2):如何維護覆蓋線段長度
先提一個小技巧,一般,利用兩個子節點來更新本節點的函式寫成PushUp();
但是,對於比較複雜的子區間合併問題,在區間查詢的時候,需要合併若干個子區間。
而合併子區間是沒辦法用PushUp函式的。於是,對於比較複雜的問題,把單個節點的資訊寫成一個結構體。
在結構體內過載運算子"+",來實現區間合併。這樣,不僅在PushUp函式可以呼叫這個加法,區間詢問時也可以
呼叫這個加法,這樣更加方便。
下面給出維護線段覆蓋長度的節點定義:
- //
- struct Node{
- int Cover;//區間整體被覆蓋的次數
- int L;//Length : 所代表的區間總長度
- int CL;//Cover Length :實際覆蓋長度
- Node operator +(const Node &B)const{
- Node X;
- X.Cover=0;//因為若上級的Cover不為0,不會呼叫子區間加法函式
- X.L=L+B.L;
- X.CL=CL+B.CL;
- return X;
- }
- }K[maxn<<2];
這樣定義之後,區間的資訊更新是這樣的:
若本區間的覆蓋次數大於0,那麼令CL=L,直接為全覆蓋,不管下層是怎麼覆蓋的,反正本區間已經全被覆蓋。
若本區間的覆蓋次數等於0,那麼呼叫上面結構體中的加法函式,利用子區間的覆蓋來計算。
加入一條線段就是給每一個分解的子區間的Cover+1,刪除線段就-1,每次修改Cover之後,更新區間資訊。
這裡完全沒有下推標記的過程。
查詢的程式碼如下:
如果不把區間加法定義成結構體內部的函式,而是定義在PushUp函式內,那麼這裡幾乎就要重寫一遍區間合併。
因為PushUp在這裡用不上。
- //
- Node Query(int L,int R,int l,int r,int rt){
- if(L <= l && r <= R){
- return K[rt];
- }
- int m=(l+r)>>1;
- Node LANS,RANS;
- int X=0;
- if(L <= m) LANS=Query(L,R,ls),X+=1;
- if(R > m) RANS=Query(L,R,rs),X+=2;
- if(X==1) return LANS;
- if(X==2) return RANS;
- return LANS+RANS;
- }
維護線段覆蓋3次或以上的長度:
- //
- struct Nodes{
- int C;//Cover
- int CL[4];//CoverLength[0~3]
- //CL[i]表示被覆蓋了大於等於i次的線段長度,CL[0]其實就是線段總長
- }ST[maxn<<2];
- void PushUp(int rt){
- for(int i=1;i<=3;++i){
- if(ST[rt].C < i) ST[rt].CL[i]=ST[rt<<1].CL[i-ST[rt].C]+ST[rt<<1|1].CL[i-ST[rt].C];
- else ST[rt].CL[i]=ST[rt].CL[0];
- }
- }
這裡給出節點定義和PushUp().
更新節點資訊的思路大概就是:
假設要更新CL[3],然後發現本節點被覆蓋了2次,那麼本節點被覆蓋三次或以上的長度就等於子節點被覆蓋了1次或以上的長度之和。
而CL[0]建樹時就賦值,之後不需要修改。
(3):如何維護掃描線過程中線段的數量
- //
- struct Node{
- int cover;//完全覆蓋層數
- int lines;//分成多少個線段
- bool L,R;//左右端點是否被覆蓋
- Node operator +(const Node &B){//連續區間的合併
- Node C;
- C.cover=0;
- C.lines=lines+B.lines-(R&&B.L);
- C.L=L;C.R=B.R;
- return C;
- }
- }K[maxn<<2];
要維護被分成多少個線段,就需要記錄左右端點是否被覆蓋,知道了這個,就可以合併區間了。
左右兩個區間合併時,若左區間的最右側有線段且右區間的最左側也有線段,那麼這兩個線段會合二為一,於是匯流排段數量會少1.
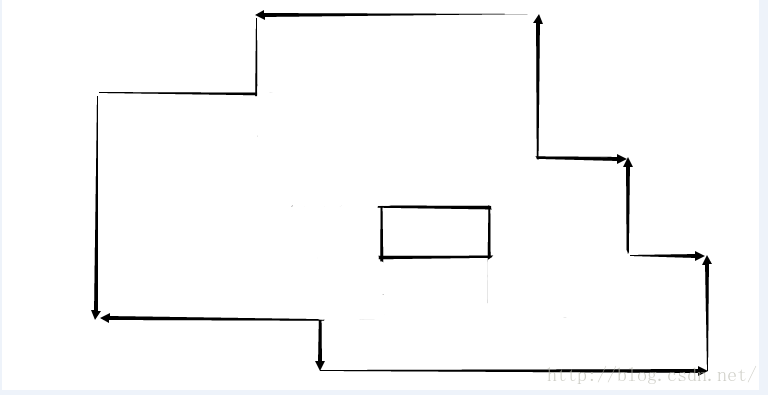
掃描線求重疊矩形周長:
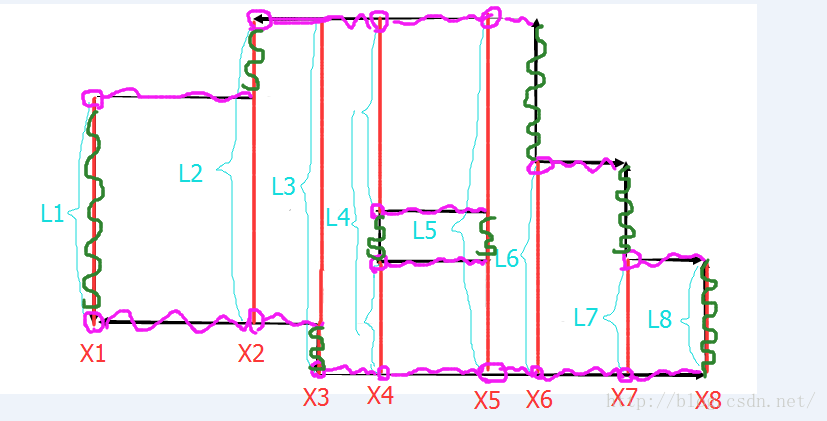
這個圖是在原來的基礎上多畫了一些東西,這次是要求周長。
所有的橫向邊都畫了紫色,所有的縱向邊畫了綠色。
先考慮綠色的邊,由圖可以觀察到,綠色邊的長度其實就是L的變化值。
比如考慮X1,本來L是0,從0變到L1,所以綠色邊長為L1.
再考慮X2,由L1變成了L2,所以綠色邊長度為L2-L1,
於是,綠色邊的長度就是L的變化值(注意上圖中令L0=0,L9=0)。
因為長度是從0開始變化,最終歸0.
再考慮紫色的邊,要計算紫色邊,其實就是計算L的線段是有幾個線段組成的,每個線段會貢獻兩個端點(紫色圓圈)
而每個端點都會向右延伸出一條紫色邊一直到下一個X值。
所以周長就是以上兩部分的和。而兩部分怎麼維護,前面都講過了,下面給出程式碼。
- //
- struct Node{
- int cover;//完全覆蓋層數
- int lines;//分成多少個線段
- bool L,R;//左右端點是否被覆蓋
- int CoverLength;//覆蓋長度
- int Length;//總長度
- Node(){}
- Node(int cover,int lines,bool L,bool R,int CoverLength):cover(cover),lines(lines),L(L),R(R),CoverLength(CoverLength){}
- Node operator +(const Node &B){//連續區間的合併
- Node C;
- C.cover=0;
- C.lines=lines+B.lines-(R&&B.L);
- C.CoverLength=CoverLength+B.CoverLength;
- C.L=L;C.R=B.R;
- C.Length=Length+B.Length;
- return C;
- }
- }K[maxn<<2];
- void PushUp(int rt){//更新非葉節點
- if(K[rt].cover){
- K[rt].CoverLength=K[rt].Length;
- K[rt].L=K[rt].R=K[rt].lines=1;
- }
- else{
- K[rt]=K[rt<<1]+K[rt<<1|1];
- }
- }
掃描的程式碼:
- int PreX=L[0].x;//前X座標
- int ANS=0;//目前累計答案
- int PreLength=0;//前線段總長
- int PreLines=0;//前線段數量
- Build(1,20001,1);
- for(int i=0;i<nL;++i){
- //操作
- if(L[i].c) Cover(L[i].y1,L[i].y2-1,1,20001,1);
- else Uncover(L[i].y1,L[i].y2-1,1,20001,1);
- //更新橫向的邊界
- ANS+=2*PreLines*(L[i].x-PreX);
- PreLines=K[1].lines;
- PreX=L[i].x;
- //更新縱向邊界
- ANS+=abs(K[1].CoverLength-PreLength);
- PreLength=K[1].CoverLength;
- }
- //輸出答案
- printf("%d\n",ANS);
求立方體重疊3次或以上的體積:
這個首先掃描面,每個面內求重疊了3次或以上的面積,然後乘以移動距離就是體積。
面內掃描線,用線段樹維護重疊了3次或以上的線段長度,然後用長度乘移動距離就是重疊了3次或以上的面積。
掃描面基本原理都跟掃描線一樣,就是嵌套了一層而已,寫的時候細心一點就沒問題了。
八:可持久化 (主席樹)
可持久化線段樹,也叫主席樹。
可持久化資料結構思想,就是保留整個操作的歷史,即,對一個線段樹進行操作之後,保留訪問操作前的線段樹的能力。
最簡單的方法,每操作一次,建立一顆新樹。這樣對空間的需求會很大。
而注意到,對於點修改,每次操作最多影響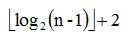
而且只有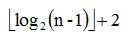
這樣,每次操作,會增加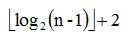
於是,這樣的線段樹,每次操作需要O(log2(n))的空間。
題目:HDU 2665 Kth number 題解
給定10萬個數,10萬個詢問。
每個詢問,問區間[L,R]中的數,從小到大排列的話,第k個數是什麼。
這個題,首先對十萬個數進行離散化,然後用線段樹來維護數字出現的次數。
每個節點都存出現次數,那麼查詢時,若左節點的數的個數>=k,就往左子樹遞迴,否則往右子樹遞迴。
一直到葉節點,就找到了第k大的數。
這題的問題是,怎麼得到一個區間的每個數出現次數。
注意到,數字的出現次數是滿足區間減法的。
於是要求區間[L,R]的數,其實就是T[R]-T[L-1] ,其中T[X]表示區間[1,X]的數形成的線段樹。
現在的問題就是,如何建立這10萬個線段樹。
由之前的分析,需要O(n log2(n))的空間
下面是程式碼:
- //主席樹
- int L[maxnn],R[maxnn],Sum[maxnn],T[maxn],TP;//左右子樹,總和,樹根,指標
- void Add(int &rt,int l,int r,int x){//建立新樹,l,r是區間, x是新加入的數字的排名
- ++TP;L[TP]=L[rt];R[TP]=R[rt];Sum[