在大多數情況下，${P_G}$和${P_{data}}$訓練到最後是不會重疊的。因為有兩點。 1.data本質：${P_G}$和${P_{data}}$是高維空間中的低維合成，這個重疊幾乎是可以忽略的。（開始訓練時） 2.從Sample角度來說，Sample兩個部分，這兩個部分交疊的部分也比較少。 當${P_G}$和${P_{data}}$沒有重疊的時候，用JS散度看它們之間的差異會在train的過程造成很大的障礙。 完全不重疊時，JS divergence=log2,下圖最後一張圖表示完全重疊。 下圖表示，一開始不重疊時，JS divergence=log2,雖然第二張圖距離近些，但仍是JS divergence=log2，而且第一張圖因為JS divergence等於常數就無法迭代到第二張圖。更無法迭代到第三張圖。 當兩者沒有重疊時，二維分類器就可以完全辨別出這兩者，最後的出來的目標函式值也會是相同的。

當很平的時候，就迭代不了了。（有點像梯度消失） 解決方法：LSGAN就是把sigmod換成linear。 positive值越接近1越好，negtive值越接近0越好。 把P這抔土移到Q的平均距離，如果P到Q的distance恆為d,那麼Earth Mover’s Distance為1。 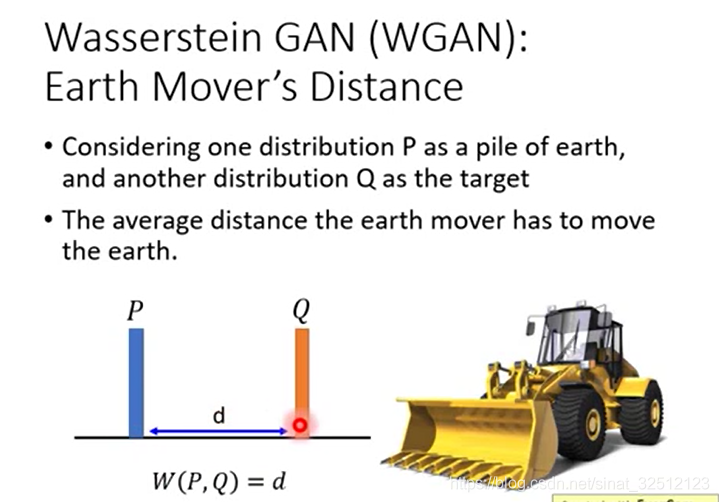但當不恆定的時候，要使兩者分佈相同，可以有不同的方法。但哪一種才是所需要的？ 窮舉出每個方法所需要的距離，最小的即為最優。 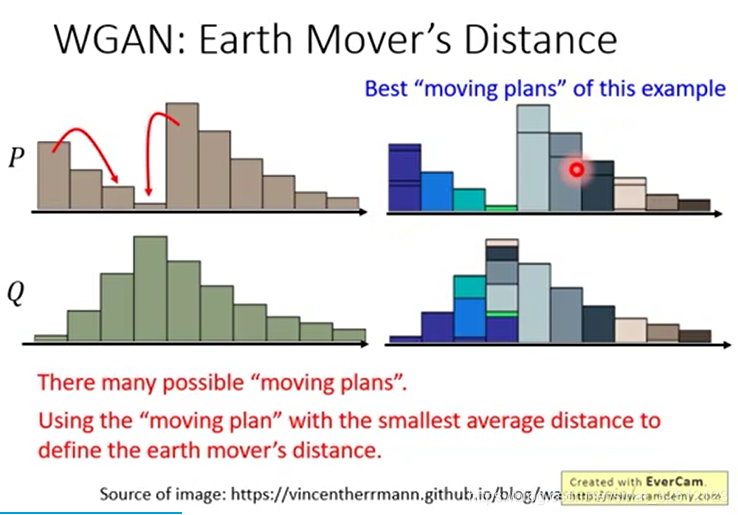更正規的表達方式如下圖 每一個方塊表示要把對應的P拿多少移到對應的Q，越亮表示移動越多。 （為什麼一行或一排合起來就是高度？） $\gamma ({x_p},{x_q})$

表示要從${x_p}$拿多少${x_q}$，$||{x_p} - {x_q}||$表示兩者間距離 窮舉$\gamma$,看哪個$\gamma$讓$W(P,Q)$最小，這個最小的距離$W(P,Q)$即為the best plan