從零開始學習PYTHON3講義(五)while迴圈和棋盤麥粒問題

《從零開始PYTHON3》第五講
上一節課重點學習了字串,並且傳遞了一個重要的理念,就是程式要對開發人員自己和使用者都足夠友好。在這個過程中,利用字串給出充分、完整、準確的提示是非常重要的一部分。
在Python可以處理的不同資料型別中,每種資料型別都有自己特色的運算方式,比如我們上一節課對比過的數字型別和字串型別的運算:
#數值的運算
>>> 123*3
369
#字串的運算
>>> "123"*3
'123123123'兩者的計算方式截然的不同,又具有自己的特點和不同的應用場景。這裡講這個例子,並不只是想讓大家複習上一講的課程。而是想讓大家思考一下計算機最擅長的工作是什麼?
沒錯,相信大多數人都想到了,計算機最擅長的,一是計算,二是重複。至於繪圖、音樂、視訊等等所謂的高階應用,不過是計算、重複的各種複雜組合。
計算在第二、第三講我們已經說過很多了,後面還會涉及到更高階的一些計算類應用。“重複”則是今天要說到的重點。
While迴圈
第三講的時候我們學過了計算機執行順序的問題。
每個Python程式都是從第一行開始,順序執行,直到程式的最後一句。其中碰到函式定義的時候,會“定義一個函式”,而不是“執行一個函式”。函式真正執行會在函式被呼叫的時候。
While迴圈則是讓計算機對某一段的程式程式碼在限定條件下重複執行的手段。我們來看一個簡單的例子來幫助我們理解:
i = 1
while i <= 999:
i = i + 1第一行,我們定義了一個變數i,併為它賦一個數字型別的值1。
第二行是while迴圈的條件部分,用於控制進入迴圈和繼續迴圈的條件。簡單說,就是當條件滿足的才開始迴圈,並且不斷迴圈下去,直到條件不再被滿足。
“<=”是條件,表示“小於等於”,同樣是因為計算機中沒有傳統用的“≤”符號,所以採用了變通的寫法。關於條件,或者說條件邏輯,我們會在後面詳細講解。
第三行是一條賦值語句,第二講我們講到變數的時候已經強調過,“=”是賦值操作符,表示把右側表示式的結果值,賦給左側的變數。
不要跟數學的等式弄混。在這裡則是把i當前值,加1的計算結果,賦值給變數i,這時候i的值變成了新的值,也是剛才的計算結果。
我們是頭一次見到這種寫法,但只要弄明白這個是賦值語句,不是等式,你就不會困惑了。
這是一個極度簡化的迴圈模型,第一行可以稱為初始值,通常這個初始值應當滿足迴圈開始的條件;
第二行稱為迴圈的條件判斷,用於控制迴圈的開始和結束;
第三行稱為迴圈體,迴圈體應當是迴圈真正工作的部分,因為簡化,在這個例子中我們看不到有意義的工作。i=i+1則讓迴圈持續,並最終能夠不再滿足迴圈繼續的條件,從而退出迴圈。否則迴圈會永無止境的繼續下去,這被稱為“死迴圈”,也是計算機軟體“崩潰”、“宕機”最常見的原因。
為了幫助理解,我們來看一個迴圈的流程圖。
流程圖是研究、分析程式結構的時候,公認非常有效的一種手段。建議你也學習畫,初學者不用糾結流程圖的樣式,而是用這種方式幫你分析程式邏輯方面的問題。
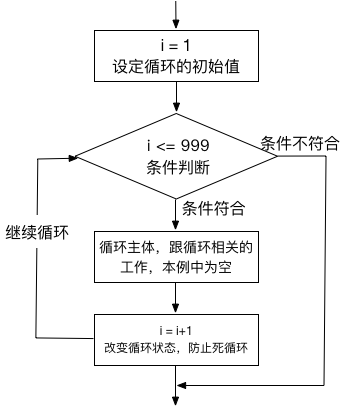
弄明白了迴圈的邏輯含義,我們再來看一下while迴圈語法上的特點,我們對比一下函式定義的語法:
#函式定義
def 函式名(引數):
函式體
#while迴圈
while 迴圈條件:
迴圈體上面這種描述程式邏輯的方法,看起來結構清楚,能反映出來想描述的程式問題,但並不能執行。這種方式叫做“虛擬碼”,是跟“程式流程圖”一樣用來分析、研究程式邏輯的方法,我們以後還會用到。
上面這個對比中,你能感覺到一些Python語法的邏輯規律。比如,都是用某個關鍵字開始,來引導整個程式塊,函式定義是用def,while迴圈是用while;接著是各自特色的東西,比如函式名、引數還有迴圈條件,相似的,都是是用冒號“:”來結尾第一行,並分割下面的函式體、迴圈體部分;後面甭管是函式體還是迴圈體,都是縮格書寫,縮格的結束代表整個程式塊的完成。
迴圈體中的賦值操作值得重點說一下。前面已經說過了,通過對可以影響迴圈條件的變數進行賦值,從而讓迴圈本身有機會退出迴圈,這是很重要的一個工作。這種賦值改變迴圈條件,幾乎在所有的迴圈中都會用到。所以這種通過對自身的改變完成對自身賦值的方式,又延伸出了一種簡易的寫法:
| 原有寫法: | 簡易寫法: |
|---|---|
| i = i + 1 | i += 1 |
| i = i -1 | i -= 1 |
| i = i * 2 | i *= 2 |
| i = i / 2 | i /= 2 |
請看上表中,左側是規範的寫法,右側是化簡後的寫法,使用起來會更方便。本質上,這是增加了+=、-=、*=、/=,四種運算賦值符,屬於保留字的一種。通常我們見到的加減乘除運算子都是一個字元,這裡是2個字元,看起來不習慣而已。
練習時間
請使用while迴圈的方法,求整數1、2、3......直到100的和。
請先自己思考10分鐘,可以用流程圖或者虛擬碼,有了比較明確的思路再向下看。
我們來看程式碼:
#求整數1-100的和
#求和的結果儲存在c,一開始是0
c = 0
#i儲存整數1迴圈到100
i = 1
#進入及繼續迴圈的條件就是i<=100
while i <= 100:
c = c + i #求和一次
i = i + 1 #下一個整數,2/3/4...
#顯示結果
print("整數1-100的和為:",c)程式中,我們使用了專門的一個變數c來儲存累加的和,一開始沒有開始累加,所以c是0。變數i通過迴圈的方式,來模擬整數從1開始,每次加1,直到100的變化。迴圈的主體c=c+i,則是在每次迴圈中,進行一次求和的操作。最後縮格結束,表示迴圈的結束,使用print函式打印出來求和結果。運算結果是:
整數1-100的和為: 5050作為練習,你可以試試把迴圈中的兩次賦值,用剛才講過的簡寫的方式來試試。
條件判斷(邏輯判斷)
對於一個迴圈來說,迴圈主體當然是迴圈的目的,所以通常也是迴圈的重點。但是在迴圈編寫的時候,仔細的思考和設定迴圈的開始條件和結束的條件,才是編寫迴圈的重點。而條件,通常都是由“邏輯判斷”來完成的。
不同於數字和字串的千變萬化,邏輯條件只有“符合條件”和“不符合條件”兩種情況。
前者的同義詞可以為“是”、“真”、“對”,後者的同義詞是“否”、“假”、“錯”。
這種只有兩個值的型別,叫“布林型別”,相關的運算叫“布林運算”。在Python中,提供了數字(Number)型別的子型別(bool)來代表此類資料。bool型別只有兩個值,True表示真,False表示假。
因為bool是Number的子型別,所以如果把bool套用到Number型別中,1就代表真,0就代表假。我們用表格把這種關係再加深一下印象:
| 符合條件 | 不符合條件 |
|---|---|
| 真 | 假 |
| true | false |
| 1 | 0 |
| "abc"(有內容) | ""(無內容,空串) |
表格中最後一行,是字串型別。對應到bool型別的情況,通常應當比較少用。但你得知道,如果字串為空代表False,有字元,甭管是什麼字元,都是True。
既然布林型別,同數字、同字串,都有對應的關係,有必要單獨獨立出來一種資料型別來增加學習量嗎?還真的是很有必要,我們來看一個例子。
比如在一個學生資訊表中,在性別一欄,我們可以使用“男”、“女”,也可以用數字1、2。看起來也可以很完美的實現我們的目的,但其實這種做法很不可取。
你想象一下在表格的輸入中,有人輸入成了“男生”,意思沒有變,但這一點小的改變,可能讓計算機無所適從。比如數字敲錯成了“3”,計算機同樣也就無法知道這代表的究竟是什麼性別。
如果使用布林變數,isMan=True代表男生,剛才碰到的那些問題,都不會出現。
此外布林運算作為數學中重要的一個分支,有完備的理論體系,在計算機中也有計算速度快、相容性好的優點。
剛才講的是“邏輯”的表達方式,下面看看邏輯判斷的方式:
| 比較運算子 | 含義 |
|---|---|
| > | 大於 |
| >= | 大於等於 |
| < | 小於 |
| <= | 小於等於 |
| == | 等於(注意同賦值操作=區分) |
| != | 不等於 |
上表中,大於、大於等於、小於、小於等於都好記。邏輯相等的判斷,要跟賦值操作的等號區別開,因為這是完全不同的運算子,或者說是不同的Python關鍵字。
不等於符號,同樣是由於計算機中沒有“≠”符號的原因進行了合理的變化。這些都是運算子,運算子不一定只有一個字元。
下面我們來看幾個邏輯判斷的例子:
| 邏輯判斷表示式 | 結果 |
|---|---|
| 1 < 2 | |
| 1 > 2 | |
| 2.2 != 2.1 | |
| "a" > "b" | |
| "bcd" < "bd" | |
| a="hello" | |
| a == "hello" | |
| 2 = 2 |
請思考後,在本講結尾看答案。
除了這些常用的邏輯判斷,Python還有自己的特色的一種判斷方式,叫做連續判斷,這是其它常見的程式語言不具備的:
| 邏輯判斷表示式 | 結果 |
|---|---|
| 1 < 2 < 7 | True |
| 1 > 2 > 1 | False |
連續判斷經常用於對一個數據進行範圍界定性判斷,所以經常也被稱為“範圍判斷”。
挑戰:棋盤麥粒問題
在古代有一個國王,他擁有至高無上的權力和難以計數的財富。但是權力和財富最終使他對生活感到厭倦,渴望著有新鮮的刺激。
某天,一位老人帶著自己發明的國際象棋來朝見。國王對這新奇的玩意非常喜歡,非常迷戀,並感到非常滿足。
於是對老人說:“你給了我無窮的樂趣。為了獎賞你,你可以從我這兒得到你所要的任何東西”。
老人的要求是:請您在棋盤上的第一個格子上放1粒麥子,第二個格子上放2粒,第三個格子上放4粒,第四個格子上放8粒……即每一個次序在後的格子中放的麥粒都必須是前一個格子麥粒數目的倍數,直到最後一個格子放滿為止。
國王哈哈大笑,慷慨地答應了老人這個卑微的請求。
然而,國王最終發現,按照與老人的約定,全國的麥子竟然連棋盤一小半格子數目都不夠。
老人索要的麥粒數目實際上是天文數字,總數將是一個十九位數,折算重量約為2000多億噸,即使現代,全球小麥的年產量也不過是數億噸。
我們要使用while迴圈作為主體,來幫助國王算一下,放滿一個國際象棋棋盤,究竟需要多少粒麥子。
同樣,請先仔細進行思考,可以使用流程圖或者虛擬碼的方式,有了比較清晰的思路再向下看。如果只是看看答案,缺少了思考,你很難真正掌握一門程式語言。
看起來很長的一個問題,其實用程式解決起來無比的容易。當然對於初學者來講,有一個清晰的思路比什麼都重要。不然就好像看心靈雞湯文,看了很多的道理,但仍然過不好這一生。
這裡介紹一種很常用的設計方法,叫做“快速原型法”。快速原型法其實並不是指什麼特定的概念。其核心思想是,把需求先弄清楚,在整理需求的過程中,通過常識性的思考,快速的把已知的部分羅列出來,不能很快弄明白的可以先空著,直到最後,逐步將空白的部分填補完成,這時候形成的其實是虛擬碼。最後用程式代替所有的虛擬碼,形成最終的結果。
說起來容易,真正實踐起來,還是需要很多的經驗磨礪,才能得心應手。不過你先有一個概念就好,逐步的多讀程式,多練習編寫程式,就能做到。
下面我們也嘗試用這種方法來編寫這個程式:
1.理清需求。我們直接把需求寫到程式的註釋中:
"""
國際象棋有8行8列共64格,
第1個格子放1粒麥子,第2個格子放2粒麥子,
以後每格都比前面格子數量多一倍,
求麥子總數。
"""你看,那麼長的文字,真正理順弄清楚,真正對程式有影響的,並不多。
2.想想在迴圈之前,我們都應當有什麼初始的值要先考慮?
#定義一個變數來儲存總的麥子數量,開始為0
c=0
#定義一個變數,迴圈1-64,來代表每一個格子
i=1
#假設每個格子中的麥子數量為x,初始也是1
x=1這一步就相當於迴圈的初始值,雖然只有i是用來控制迴圈,但既然我們用迴圈來幫助運算,那每一個跟迴圈有關的變數,不可能沒有初始值。
3.迴圈的過程部分,思考起來,似乎有點複雜,我們先想迴圈結束應當是什麼?當然是顯示結果:
#顯示結果
print("64個格子,總的麥粒數量為:",c)4.雖然迴圈比較複雜,但就剩這一部分了,也不得不開始考慮。首先考慮迴圈的進入和退出條件。迴圈是從第一個格子,迴圈到第64個格子,因為包含第64個格子本身,所以迴圈條件肯定是<=64,如果是<64,那迴圈到第63個格子就結束了:
while i<=64:5.迴圈的邊界條件定義好了,現在考慮真正的計算,也就是迴圈體的部分:
c += x #總數 累計上 這一個格子的麥粒數
i += 1 #下一個格子
x = x*2 #下一個格子的麥粒數是這一個格子的2倍其實總共就是這樣三行不能再少的運算。注意這裡我們都使用了變數自身賦值的簡寫形式。
還有一點就是我們前面的例子都是把i = i+1放到迴圈體最後,其實這並不是必須的,只要在迴圈體中修改了迴圈條件相關的變數,不會導致死迴圈就可以。在哪裡為迴圈變數賦值,是程式人員根據方便程度決定的。
好了,完整的貼一遍程式:
"""
國際象棋有8行8列共64格,
第1個格子放1粒麥子,第2個格子放2粒麥子,
以後每格都比前面格子數量多一倍,
求最終麥子總數。
"""
#定義一個變數來儲存總的麥子數量,開始為0
c=0
#定義一個變數,迴圈1-64,來代表每一個格子
i=1
#假設每個格子中的麥子數量為x,初始也是1
x=1
#迴圈
while i<=64:
c += x #總數累計上這一個格子的麥粒數
i += 1 #下一個格子
x = x*2 #下一個格子的麥粒數是這一個格子的2倍
#顯示結果
print("64個格子,總的麥粒數量為:",c)執行的結果一定要自己把程式輸入進去之後,自己看一看。
練習時間
練習1:由使用者輸入一個整數n,用while迴圈求整數1直至n的和。(提示,上一講介紹過函式input())
練習2:請將練習1的程式函式化,要求求和部分單獨為一個函式。
練習3:請將棋盤麥粒問題函式化,以便求出1至指定格子的麥粒數量總和。因為過大的數字會超出Python的計算範圍,我們假定允許使用者輸入的格子為1-64。
本講小結
- 計算機適合做枯燥、重複、大量的工作,迴圈在這種情況下起著重要的作用。while迴圈是較為自由的一種迴圈方式,用途很廣泛
- 迴圈的初始值和邊界條件非常重要,讓計算機執行正確,自己需要先設想自己處於計算機的位置上,想清楚
- 迴圈的邊界條件必須是可以變化的,需要迴圈的時候能迴圈,需要退出迴圈的時候要能變化條件,所以只能是變數
- 判斷邊界條件,需要使用“比較運算子”
- 比較運算子返回的是布林值:True(真)、False(假),因為有了布林值,計算機才能區別於計算器。特別注意區別比較運算的相等符號和賦值命令的等號
參考答案
中間的判斷表示式及其結果:
| 邏輯判斷表示式 | 結果 |
|---|---|
| 1 < 2 | True |
| 1 > 2 | False |
| 2.2 != 2.1 | True |
| "a" > "b" | False |
| "bcd" < "bd" | True |
| a="hello" | 賦值表示式,不能當做邏輯條件使用 |
| a == "hello" | True |
| 2 = 2 | 錯誤:2是字元,不是變數,不能被賦值 |
最後的三個練習請參考原始碼ex1.py/ex2.py/ex3.py
