一直以來對於貝葉斯聽的很多，但是記憶中僅有的只是一個貝葉斯的公式。最近自學機器學習的演算法，看到了很多貝葉斯分類器的文章視屏，現在終於對貝葉斯有了一個深入的瞭解。下面是我自己在學習之後的認識，寫一個學習筆記吧，當作自己的備忘錄。如有錯誤，歡迎批評指正。

1、貝葉斯公式是什麼？

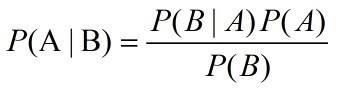
這之中P（A|B）和P（B|A）叫後驗概率，而P（A）和P（B）叫先驗概率；後驗概率指的是某一件事情發生時候需要考慮到其它的因素，而先驗概率指的是某個事件發生時候不需要考慮其它的因素。

2、貝葉斯公式意義？

貝葉斯公式就是一個求概率的公式，假如用P(A)代表起火的概率，P（B）代表消防警報響的概率，P(B|A)代表在起火後響起消防警報的概率，而P(A|B)代表在消防警報響起後發生火災的概率，一般情況下P(B|A)，P(A|B)是不相等的，試想一下，消防警報響了有可能是人為誤觸的情況，也有可能是裝置故障的情況，也有可能是消防演習；而起火後很大概率消防警報都會響起；這個時候，我們就可以用P(A)代表起火的概率，P（B）代表消防警報響的概率，P(B|A)代表在起火後響起消防警報的概率，去估計消防警報響起了是否是真的起火。

3、貝葉斯公式可以幹什麼？

首先，貝葉斯公式可以用來計算一個概率，當然了，它也可以用來做分類問題，通俗的理解就是：有一些樣本，我們需要根據特徵來估計它的來別

4、使用貝葉斯公式如何分類？

貝葉斯分類的理解：這個時候，我們可以理解為P(A)代表某一類別出現的概率，P（B）代表的是某一特徵出線的概率，P(B|A)代表在某一來別某個特徵出出的概率，而P(A|B)代表某一特徵出現了，那麼它屬於這一類別的的概率，我們可以對於某一個特徵求它屬於各個類別的概率，從而去概率最大值對應的類別就是該樣本對應的類別。這裡認為B是特徵，A是類別。

貝葉斯分類的實現過程：用到樸素貝葉斯

一般情況下：某一個樣本的特徵是由不同的屬性值構成    B=(b1​,b2​,b3​,...,bn​)，根據貝葉斯的思想，是需要從樣本中去估計P(B|A)，P（B）和P(A)，但是所有類別P(A|B)判斷時候分母都是一樣的，所以P（B）可以先不用管，而P（A）就是用每個類別中的樣本個數除以總的樣本數；依據大叔定理，現在P(B|A)估計就很難了，因為對於樣本的特徵B=(b1​,b2​,b3​,...,bn​)，它由不同的屬性值組成，最初的設想就是用某個特徵出現的樣本數除以總樣本數類獲得，但是我們拿到的樣本往往是有限的，當特徵較多時候，不同的屬性組成的特徵每個只出現一次就需要龐大的樣本，更不用說出現很多次對其進行估計了，如果用少的樣本去估計，那麼很多的這個時候P(B|A)都是0，我們就想能不能用現有的樣本的去做一些代替，這個時候就出現了樸素貝葉斯。

5、樸素貝葉斯

樸素貝葉斯認為對於每個特徵中各個屬性值的出現是獨立的，互不影響的，之前我們需要求的是P(B|A)即P(b1​,b2​,b3​,...,bn|A)，即用每個特徵出現的次數除以樣本數，但是事實證明這樣是行不通的。為此，我們想著對於P(b1​,b2​,b3​,...,bn|A)聯合概率能不能用另一宗方式求，這時候樸素貝葉斯假設各個條件是獨立的，那麼就可以用P(b1|A)*P(b2​|A)*P(b3​|A)*...*P(bn|A)來表示P(b1​,b2​,b3​,...,bn|A，而P(b1|A)，就可以根據樣本很好的估計了。這個時候就可以根據其原理實現分類了。

6、樸素貝葉斯究竟幫我們幹了什麼事？

我們的樣本數量不能夠支援我們直接去用樣本除以總體的方式計算P(B|A)即P(b1​,b2​,b3​,...,bn|A)，其次，樣本特徵內在特性是特徵中不同的屬性值往往是有聯絡的，我們希望能過用有限的樣本去估計P(B|A)，這個時候，我們用過樸素貝葉斯的假設來破壞特性之間的關係使其獨立，從而便於我們用更簡便的方式去計算P(b1​,b2​,b3​,...,bn|A)，總而言之就是為了用有限的樣本去計算P(B|A)破壞屬性的關係，計算概率是目的；破壞屬性的關係是其實現的方式，服務於概率的計算