《統計學習方法(李航)》樸素貝葉斯學習筆記
作者:jliang
1.重點歸納
1)樸素貝葉斯(naive Bayes)法只能用於分類,先基於特徵條件獨立假設學習輸入/輸出的聯合概率分佈,然後對給定的輸入x,利用貝葉斯定理求出後驗概率最大的輸出y。
2)損失函式:0-1損失函式
3)目標函式:後驗概率最大化

4)屬於生成式模型
5)聯合概率分佈:![]()
6)貝葉斯公式:
7)貝葉斯引數可使用極大似然估計,但是用極大似然估計可能會出現所要估計的概率值為0的情況,這是會影響後驗概率的計算結果,使分類偏差。所以引入貝葉斯估計:
(1)條件概率計算公式:

(2)先驗概率公式:![]()
8)貝葉斯型別
- 高斯樸素貝葉斯(GaussianNB):適用於一般分類
- 多項式分佈樸素貝葉斯(MultinomialNB):適用於文字資料(特徵表示的是次數)
- 伯努利分佈樸素貝葉斯(BernoulliNB):適用於伯努利分佈,也適用於文字資料。用於文字時,特徵表示是否出現。
2.樸素貝葉斯的學習與分類
1)樸素貝葉斯(naive Bayes)法是基於貝葉斯定理與特徵條件獨立假設的分類方法。
(1)只能用於分類。分類步驟:
- 基於特徵條件獨立假設學習輸入/輸出的聯合概率分佈
- 基於此模型,對給定的輸入x,利用貝葉斯定理求出後驗概率最大的輸出y
(2)損失函式:0-1損失函式
(3)目標函式:後驗概率最大化
(4)生成式模型
2)貝葉斯法對條件概率分佈作了條件獨立性的假設(前提),條件獨立性假設使貝葉斯變得簡單,但有時會犧牲一定的分類準確性。
3)聯合概率分佈:![]()
4) 貝葉斯公式:![]()
預測模型:P類別特徵=P(類別)P(特徵|類別)P特徵
兩個條件時:![]()
多個條件時:![]()
5)目標函式(後驗概率最大化),後驗概率最大等價於0-1損失函式時的期望風險最小化。

3. 樸素貝葉斯的的引數估計
1)極大似然估計:就是在假定整體模型分佈已知,利用已知的樣本結果資訊,反推最具有可能(最大概率)導致樣本結果出現的模型引數值。
(1)先驗概率:![]()
(2)條件概率:![]()
特徵維數量:j=1,2,…,n
每個特徵可取值數量:l=1,2,…,Sj
標籤型別數量:k=1,2,…,K
2)樸素貝葉斯演算法計算步驟
(1)計算先驗概率和條件概率
(2)計算給定例項(輸入特徵)對應的每種取值的後驗概率
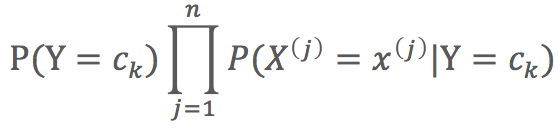
(3)確定例項的類別(上一步中概率最大值即為輸出類別)
3)貝葉斯估計
(1)使用原因:用極大似然估計可能會出現所要估計的概率值為0的情況,這是會影響後驗概率的計算結果,使分類偏差。
(2)條件概率的貝葉斯估計估計
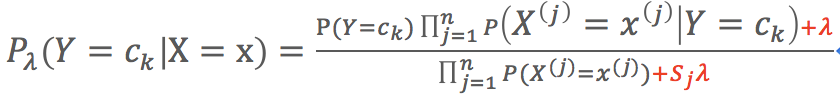
- 相對於極大似然估計,貝葉斯估計公式中分子多了一個λ,分母多了一個Sjλ
- λ≥0
- λ=0,為極大似然估計
- λ=1,為拉普拉斯平滑
- Sj為特徵Xj的取值數
(3)先驗概率的貝葉斯估計
![]()
- 相對於極大似然估計,貝葉斯公式中分子多了一個λ,分母多了一個Kλ
- K為y的取值數
4.樸素貝葉斯型別
1)高斯樸素貝葉斯(GaussianNB)
- 高斯分佈是正太分佈,用於一般分類問題。
2)多項式分佈樸素貝葉斯(MultinomialNB)
- 多項式分佈:
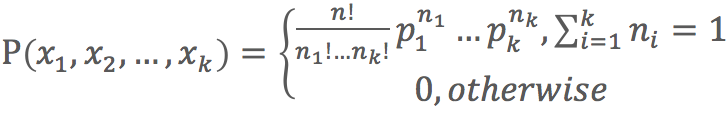
- 適用於文字資料(特徵表示的是次數,例如某個次數的出現的頻率)。
3)伯努利分佈樸素貝葉斯(BernoulliNB)
- 伯努利分佈:

- 適用於伯努利分佈,也適用於文字資料。用於文字時,特徵表示是否出現,例如某個詞出現為1,否則為0。
- 絕大多數情況下伯努利分佈樸素貝葉斯不如多項式分佈樸素貝葉斯,但有時候伯努利分佈樸素貝葉斯表現要比多項式分佈要好,尤其是對於小數量級的文字資料。
