2. 程式人生 > >STL原始碼剖析---紅黑樹原理詳解下

STL原始碼剖析---紅黑樹原理詳解下

阿新 • • 發佈：2018-12-20
                轉載請標明出處，原文地址：http://blog.csdn.net/hackbuteer1/article/details/7760584      演算法導論書上給出的紅黑樹的性質如下，跟STL原始碼剖析書上面的4條性質大同小異。      1、每個結點或是紅色的，或是黑色的      2、根節點是黑色的      3、每個葉結點（NIL）是黑色的      4、如果一個節點是紅色的，則它的兩個兒子都是黑色的。      5、對於每個結點，從該結點到其子孫結點的所有路徑上包含相同數目的黑色結點。      從紅黑樹上刪除一個節點，可以先用普通二叉搜尋樹的方法，將節點從紅黑樹上刪除掉，然後再將被破壞的紅黑性質進行恢復。      我們回憶一下普通二叉樹的節點刪除方法：Z指向需要刪除的節點，Y指向實質結構上被刪除的結點，如果Z節點只有一個子節點或沒有子節點，那麼Y就是指向Z指向的節點。如果Z節點有兩個子節點，那麼Y指向Z節點的後繼節點
（其實前趨也是一樣的），而Z的後繼節點絕對不可能有左子樹。因此，僅從結構來看，二叉樹上實質被刪除的節點最多隻可能有一個子樹。現在我們來看紅黑性質的恢復過程：      如果Y指向的節點是個紅色節點，那麼直接刪除掉Y以後，紅黑性質不會被破壞。操作結束。      如果Y指向的節點是個黑色節點，那麼就有幾條紅黑性質可能受到破壞了。首先是包含Y節點的所有路徑，黑高度都減少了一（第５條被破壞）。其次，如果Y的有紅色子節點，Y又有紅色的父節點，那麼Y被刪除後，就出現了兩個相鄰的紅色節點（第４條被破壞）。最後，如果Y指向的是根節點，而Y的子節點又是紅色的，那麼Y被刪除後，根節點就變成紅色的了（第２條被破壞）。      其中，第５條被破壞是讓我們比較難受的。因為這影響到了全域性。這樣動作就太大太複雜了。而且在這個條件下，進行其它紅黑性質的恢復也很困難。所以我們首先解決這個問題：如果不改變含Y路徑的黑高度，那麼樹的其它部分的黑高度就必須做出相應的變化來適應它。所以，我們想辦法恢復原來含Y節點的路徑的黑高度。做法就是：無條件的把Y節點的黑色，推到它的子節點X上去
。（X可能是NIL節點）。這樣，X就可能具有雙重黑色，或同時具有紅黑兩色，也就是第１條性質被破壞了。      但第１條性質是比較容易恢復的：一、如果X是同時具有紅黑兩色，那麼好辦，直接把X塗成黑色，就行了。而且這樣把所有問題都解決了。因為將X變為黑色，２、４兩條如果有問題的話也會得到恢復，演算法結束。二、如果X是雙黑色，那麼我們希望把這種情況向上推一直推到根節點（調整樹結構和顏色，X的指向新的雙黑色節點，X不斷向上移動），讓根節點具雙黑色，這時，直接把X的一層黑色去掉就行了（因為根節點被包含在所有的路徑上，所以這樣做所有路徑同時黑高減少一，不會破壞紅黑特徵）。      下面就具體地分析如何恢復1、２、４三個可能被破壞的紅黑特性：我們知道，如果X指向的節點是有紅黑兩色，或是X是根節點時，只需要簡單的對X進行一些改變就行了。要對除X節點外的其它節點進行操作時，必定是這樣的情況：X節點是雙層黑色，且X有父節點P。由知可知，X必然有兄弟節點W，而且這個W節點必定有兩個子節點。（因為這是原樹滿足紅黑條件要求而自然具備的。X為雙黑色，那麼P的另一個子節點以下一定要有至少兩層的節點，否則黑色高度不可能和X路徑一致）。所以我們就分析這些節點之間如何變形，把問題限制在比較小的範圍內解決。另一個前提是：X在一開始，肯定是樹底的葉節點或是NIL節點，所以在遞歸向上的過程中，每一步都保證下一步進行時，至少 X的子樹是滿足紅黑特性的。因此子樹的情況就可以認為是已經正確的了，這樣，分析就只限制在X節點，X的父節點P和X的兄弟節點W，以及W的兩個子節點中。      下面僅僅考慮X原本是黑色的情況即可。      在這種情況下，X此時應該具有雙重黑色，演算法的過程就是將這多出的一重黑色向上移動，直到遇到紅節點或者根節點。      接著往下分析， 會遇到4種情況，實際上是8種， 因為其中4種是相互對稱的，這可以通過判斷X是其父節
點的右孩子還是左孩子來區分。下面我們以X是其父節點的左孩子的情況來分析這4種情況，實際上接下來的調整過程，就是要想方設法將經過X的所有路徑上的黑色節點個數增加1。      具體分為以下四種情況：（下面針對x是左兒子的情況討論，右兒子對稱）     Case1：X的兄弟W是紅色（想辦法將其變為黑色）       由於W是紅色的，因此其兒子節點和父節點必為黑色，只要將W和其父節點的顏色對換，在對父節點進行一次左旋轉，便將W的左子節點放到了X的兄弟節點上，X的兄弟節點變成了黑色，且紅黑性質不變。但還不算完，只是暫時將情況1轉變成了下面的情況2或3或4。    Case2：X的兄弟節點W是黑色的，而且W的兩個子節點都是黑色的。此時可以將X的一重黑色和W的黑色同時去掉，而轉加給他們的父節點上，這是X就指向它的父節點了，因此此時父節點具有雙重顏色了。這一重黑色節點上移。      如果父節點原來是紅色的，現在又加一層黑色，那麼X現在指向的這個節點就是紅黑兩色的，直接把X（也就是父節點）著為黑色。問題就已經完整解決了。     如果父節點現在是雙層黑色，那就以父節點為新的X進行向上的下一次的遞迴。    Case3：X的兄弟節點W是黑色的，而且W的左子節點是紅色的，右子節點是黑色的。此時通過交換W和其左子節點的顏色並進行一次向右旋轉就可轉換成下面的第四種情況。注意，原來L是紅色的，所以L的子節點一定是黑色的，所以旋轉中L節點的一個子樹掛到之後著為紅色的W節點上不會破壞紅黑性質。變形後黑色高度不變。    Case4：X的兄弟節點W是黑色的，而且W的右子節點是紅色的。這種情況下，做一次左旋，W就處於根的位置，將W保持為原來的根的位置的顏色，同時將W的兩個新的兒子節點的顏色變為黑色，去掉X的一重黑色。這樣整個問題也就得到了解決。遞迴結束。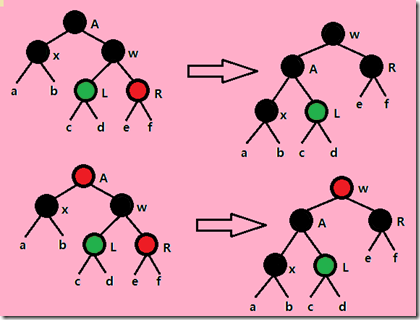（在程式碼上，為了標識遞迴結束，我們把X指向根節點）      因此，只要按上面四種情況一直遞迴處理下去，X最終總會指向根結點或一個紅色結點，這時我們就可以結束遞歸併把問題解決了。      以上就是紅黑樹的節點刪除全過程。      總結：      如果我們通過上面的情況畫出所有的分支圖，我們可以得出如下結論      插入操作：解決的是 紅-紅 問題      刪除操作：解決的是 黑-黑 問題      即你可以從分支圖中看出，需要往上遍歷的情況為紅紅(插入)，或者為黑黑黑（刪除）的情況，如果你認真分析並總結所有的情況後，並堅持下來，紅黑樹也就沒有想象中的那麼恐怖了，並且很美妙；      詳細的紅黑樹刪除節點的程式碼如下：
#include<iostream>using namespace std;// 定義節點顏色  enum COLOR{      BLACK = 0,      RED  };    // 紅黑樹節點  typedef struct RB_Tree_Node{      int key;      struct RB_Tree_Node *left;      struct RB_Tree_Node *right;      struct RB_Tree_Node *parent;      unsigned char RB_COLOR;  }RB_Node;// 紅黑樹，包含一個指向根節點的指標  typedef struct RBTree{      RB_Node* root;}*RB_Tree;// 紅黑樹的NIL節點  static RB_Tree_Node NIL = {0, 0, 0, 0, BLACK}; #define PNIL (&NIL)   // NIL節點地址 void Init_RBTree(RB_Tree pTree) // 初始化一棵紅黑樹  {      pTree->root = PNIL;  }   // 查詢最小鍵值節點  RB_Node* RBTREE_MIN(RB_Node* pRoot)  {      while (PNIL != pRoot->left)    {        pRoot = pRoot->left;    }      return pRoot;}/*                          15                        /    \                       /      \                      /        \                     6          18                    /  \       /  \                   /    \     /    \                  3      7   17    20                 /  \     \                /    \     \               2      4     13                            /                           /                          9*/// 查詢指定節點的後繼節點  RB_Node* RBTREE_SUCCESSOR(RB_Node*  pRoot)  {      if (PNIL != pRoot->right)    // 查詢圖中6的後繼節點時就呼叫RBTREE_MIN函式    {          return RBTREE_MIN(pRoot->right);      }    // 節點沒有右子樹的時候，進入下面的while迴圈（如查詢圖中13的後繼節點時，它的後繼節點是15）    RB_Node* pParent = pRoot->parent;      while((PNIL != pParent) && (pRoot == pParent->right))    {          pRoot = pParent;        pParent = pRoot->parent;          }    return pParent;}// 紅黑樹的節點刪除RB_Node* Delete(RB_Tree pTree , RB_Node* pDel)  {      RB_Node* rel_delete_point;    if(pDel->left == PNIL || pDel->right == PNIL)        rel_delete_point = pDel;    else        rel_delete_point = RBTREE_SUCCESSOR(pDel);     // 查詢後繼節點    RB_Node* delete_point_child;      if(rel_delete_point->right != PNIL)      {          delete_point_child = rel_delete_point->right;      }      else if(rel_delete_point->left != PNIL)      {          delete_point_child = rel_delete_point->left;      }      else      {          delete_point_child = PNIL;      }      delete_point_child->parent = rel_delete_point->parent;      if(rel_delete_point->parent == PNIL)    // 刪除的節點是根節點    {          pTree->root = delete_point_child;    }      else if(rel_delete_point == rel_delete_point->parent->right)    {          rel_delete_point->parent->right = delete_point_child;      }      else      {          rel_delete_point->parent->left = delete_point_child;      }    if(pDel != rel_delete_point)    {        pDel->key = rel_delete_point->key;    }    if(rel_delete_point->RB_COLOR == BLACK)      {          DeleteFixUp(pTree , delete_point_child);      }    return rel_delete_point;  }               /*演算法導論上的描述如下：RB-DELETE-FIXUP(T, x) 1 while x ≠ root[T] and color[x] = BLACK 2     do if x = left[p[x]] 3           then w ← right[p[x]] 4                if color[w] = RED 5                   then color[w] ← BLACK                           Case 1 6                        color[p[x]] ← RED                          Case 1 7                        LEFT-ROTATE(T, p[x])                       Case 1 8                        w ← right[p[x]]                            Case 1 9                if color[left[w]] = BLACK and color[right[w]] = BLACK 10                   then color[w] ← RED                            Case 2 11                        x p[x]                                    Case 2 12                   else if color[right[w]] = BLACK 13                           then color[left[w]] ← BLACK            Case 3 14                                color[w] ← RED                    Case 3 15                                RIGHT-ROTATE(T, w)                Case 3 16                                w ← right[p[x]]                   Case 3 17                         color[w] ← color[p[x]]                   Case 4 18                         color[p[x]] ← BLACK                      Case 4 19                         color[right[w]] ← BLACK                  Case 4 20                         LEFT-ROTATE(T, p[x])                     Case 4 21                         x ← root[T]                              Case 4 22        else (same as then clause with "right" and "left" exchanged) 23 color[x] ← BLACK  */  //接下來的工作，很簡單，即把上述虛擬碼改寫成c++程式碼即可  void DeleteFixUp(RB_Tree pTree , RB_Node* node)  {      while(node != pTree->root && node->RB_COLOR == BLACK)      {          if(node == node->parent->left)          {              RB_Node* brother = node->parent->right;              if(brother->RB_COLOR==RED)   //情況1：x的兄弟w是紅色的。              {                  brother->RB_COLOR = BLACK;                  node->parent->RB_COLOR = RED;                  RotateLeft(node->parent);              }              else     //情況2：x的兄弟w是黑色的，              {                  if(brother->left->RB_COLOR == BLACK && brother->right->RB_COLOR == BLACK)  //w的兩個孩子都是黑色的                  {                      brother->RB_COLOR = RED;                      node = node->parent;                  }                  else                {                    if(brother->right->RB_COLOR == BLACK)   //情況3：x的兄弟w是黑色的，w的右孩子是黑色（w的左孩子是紅色）。                      {                        brother->RB_COLOR = RED;                        brother->left->RB_COLOR = BLACK;                        RotateRight(brother);                        brother = node->parent->right;      //情況3轉換為情況4                    }                    //情況4：x的兄弟w是黑色的，且w的右孩子時紅色的                    brother->RB_COLOR = node->parent->RB_COLOR;                      node->parent->RB_COLOR = BLACK;                      brother->right->RB_COLOR = BLACK;                      RotateLeft(node->parent);                      node = pTree->root;                }//else            }//else        }          else   //同上，原理一致，只是遇到左旋改為右旋，遇到右旋改為左旋即可。其它程式碼不變。          {              RB_Node* brother = node->parent->left;              if(brother->RB_COLOR == RED)              {                  brother->RB_COLOR = BLACK;                  node->parent->RB_COLOR = RED;                  RotateRight(node->parent);              }              else              {                  if(brother->left->RB_COLOR==BLACK && brother->right->RB_COLOR == BLACK)                  {                      brother->RB_COLOR = RED;                      node = node->parent;                  }                  else                {                    if(brother->left->RB_COLOR==BLACK)                      {                          brother->RB_COLOR = RED;                          brother->right->RB_COLOR = BLACK;                          RotateLeft(brother);                        brother = node->parent->left;      //情況3轉換為情況4                    }                    brother->RB_COLOR = node->parent->RB_COLOR;                      node->parent->RB_COLOR = BLACK;                      brother->left->RB_COLOR = BLACK;                      RotateRight(node->parent);                      node = pTree->root;                  }              }          }      }//while     node->RB_COLOR = BLACK;    //如果X節點原來為紅色，那麼直接改為黑色  }
           

相關推薦

STL原始碼剖析---紅黑樹原理詳解下

                轉載請標明出處，原文地址：http://blog.csdn.net/hackbuteer1/article/details/7760584      演算法導論書上給出的紅黑樹的性質如下，跟STL原始碼剖析書上面的4條性質大同小異。      1、每個結點或是紅色的，或是黑色的

STL原始碼剖析---紅黑樹原理詳解上

                     紅黑樹和我們以前學過的AVL樹類似，都是在進行插入和刪除操作時通過特定操作保持二叉查詢樹的平衡，從而獲得較高的查詢效能。不過自從紅黑樹出來後，AVL樹就被放到了博物館裡，據說是紅黑樹有更好的效率，更高的統計效能。這一點在我們瞭解了紅黑樹的實現原理後，就會有更加深切的體

紅黑樹原理詳解及golang實現

目錄 紅黑樹原理詳解及golang實現 二叉查詢樹 性質 紅黑樹 性質 operation 紅黑樹的插入 g

STL原始碼剖析——stack的實現原理和使用方法詳解

Stack 簡介     stack 是堆疊容器，是一種“先進後出”的容器。     stack 是簡單地裝飾 deque 容器而成為另外一種容器。     使用 stack 時需要加上標頭檔案 #include<s

STL原始碼剖析——deque的實現原理和使用方法詳解

Deque 簡介     deque是“double—ended queue”的縮寫，和vector一樣都是STL的容器，deque 是雙端陣列，而 vector 是單端的。     deque 在介面上和 vector 非常相似，在許多操作的地方

紅黑樹原理淺談(附Linux核心原始碼註釋)

引言：紅黑樹（英語：Red–black tree）是一種自平衡二叉查詢樹，是在電腦科學中用到的一種資料結構，典型的用途是實現關聯陣列。它是在1972年由魯道夫·貝爾發明的，他稱之為"對稱二叉B樹"，它現代的名字是在Leo J. Guibas和Robert Sedgewick於19

二叉樹之一BST樹，AVL樹詳解及B樹和紅黑樹原理分析

BST樹，AVL樹詳解及B樹和紅黑樹原理分析 網際網路面試中樹尤其是BST，AVL是提問的重點也是難點，甚至B樹乃至高階資料結構紅黑樹都是提問的重點，像阿里雲面試就曾經問過map實現機制（紅黑樹）及其原理，這裡我們要做到對BST/AVL完全熟悉能給出全部程式碼實現，紅黑樹、

深入剖析紅黑樹以及JAVA實現

作者：美團技術團隊 連結：https://zhuanlan.zhihu.com/p/24367771 來源：知乎 著作權歸作者所有。商業轉載請聯絡作者獲得授權，非商業轉載請註明出處。   紅黑樹是平衡二叉查詢樹的一種。為了深入理解紅黑樹，我們需要從二叉查詢樹開始講起。 BST

JDK1.8中TreeMap原始碼解析——紅黑樹刪除

在看本文之前建議先看一下二叉樹的刪除過程，這裡有一篇文章寫得不錯，可以看一下 1、後繼節點 在看原始碼之前，先說說紅黑樹尋找 待刪除節點t 的 後繼節點 的過程： 如果待刪除節點t有右節點，那麼後繼節點為該節點右子樹中最左的節點，也就是右子樹中值最小的節

HashMap1.8原始碼分析(紅黑樹)

轉載：https://segmentfault.com/a/1190000012926722?utm_source=tag-newest https://blog.csdn.net/weixin_40255793/article/details/80748946(方法全面) 方法 treeifyBin(

AVL平衡二叉樹，紅黑樹原理。

二叉搜尋樹 插入和刪除操作必須先查詢，查詢效率代表了二叉搜尋樹中各個操作的效能 最優情況：二叉搜尋樹為完全二叉樹，比較次數Log2^N 最壞情況：二叉搜尋樹為單支樹，平均比較次數N/2 平衡二叉樹 平衡樹： AVL樹，紅黑樹 AVL樹：（二叉搜尋樹改良版）

紅黑樹 原理和演算法詳細介紹（Java）

R-B Tree簡介 R-B Tree，全稱是Red-Black Tree，又稱為“紅黑樹”，它一種特殊的二叉查詢樹。紅黑樹的每個節點上都有儲存位表示節點的顏色，可以是紅(Red)或黑(Black)。 紅黑樹的特性: （1）每個節點或者是黑色，或者是紅

紅黑樹原理解析以及Java實現

紅黑樹 本文的主要內容： 1、紅黑樹的基本概念以及最重要的5點規則。 2、紅黑樹的左旋轉、右旋轉、重新著色的原理與Java實現； 3、紅黑樹的增加結點、刪除結點過程解析； 1.紅黑樹的基本概念與資料結構表示 首先紅黑樹來個定義： 紅黑樹定

資料結構 — 淺析紅黑樹原理以及實現

淺析紅黑樹原理以及實現我們在上一篇部落格認識到了平衡二叉樹(AVLTree)，瞭解到平衡二叉樹的性質，其實平衡二叉樹最大的作用就是查詢,AVL樹的查詢、插入和刪除在平均和最壞情況下都是O(logn)。AVL樹的效率就是高在這個地方。如果在AVL樹中插入或刪除節點後，使得高度之

紅黑樹原理，演算法，和構建過程的分析和學習

參考文章：紅黑樹原理：此篇邏輯清晰，但是紅黑樹的配圖不行，沒法根據圖來進行實際的操作理解，本文的意圖就是根據作者的思路進行圖片的重新分析。《演算法導論》中文版，中文版翻譯的馬馬虎虎，但是有些概念翻譯的有點爛，在學習過程中會產生一些疑惑，需要及時更新自己的認知。紅黑樹特性：（1

線段樹原理詳解（單點更新 區間查詢）

這道題是線段樹的  單點更新和區間查詢最大值 （AC程式碼在最後） 通過這道題  理解下線段樹 線段樹的原理 關於原理   網上有很多講解 大家可以自己學習   這裡不單獨贅述原理 而是結合程式碼講解下   原理也不難  相信大家看了程式碼仔細看下邊的解釋可以理

紅黑樹 自頂向下插入操作（一）

1. 紅黑樹簡介：    對於紅黑樹 一種變異型的平衡二叉樹，保持最壞的情況下查詢時間的複雜度o(logN),在 紅黑樹的 插入操作過程中有兩種 方式 自頂向下插入 和 自低向上的插入；相比較而言 各自有其優點，不管 採用何種方式 在 Insert 操作中 規定：將插入結點

資料結構之紅黑樹-動圖演示(下)

節點的插入和刪除 我們知道變色和旋轉是為了修正被破壞的紅黑樹，使其符合紅黑樹的規則，從新達到平衡狀態。那麼增加或刪除節點在具體情況下該如何操作呢？ 插入節點 紅黑樹的節點插入與二叉查詢樹的插入的過程是一樣的，只是最後多了一步平衡調整操作。 新插入的節點預設為紅色節點，所以新節點插入到黑色節點下時不需要對平衡調

TreeMap紅黑樹原始碼詳解

尊重原創，轉載請標明出處   http://blog.csdn.net/abcdef314159 在分析原始碼之前，最好要標註出處，因為在Java中和Android中同一個類可能程式碼就會不一樣，甚至在Android中不同版本之間程式碼也可能會有很大的差別，下面

stl map底層之紅黑樹插入步驟詳解與程式碼實現

本篇文章並沒有詳細的講解紅黑樹各方面的知識，只是以圖形的方式對紅黑樹插入節點需要進行調整的過程進行的解釋。 最近在看stl原始碼剖析，看到map底層紅黑樹的實現。為了加深對於紅黑樹的理解就自己動手寫了紅黑樹插入的實現。關於紅黑樹插入節點後破壞紅黑樹性質的幾種情況，可以在網