紅黑樹

本文的主要內容：
1、紅黑樹的基本概念以及最重要的5點規則。
2、紅黑樹的左旋轉、右旋轉、重新著色的原理與Java實現；
3、紅黑樹的增加結點、刪除結點過程解析；

1.紅黑樹的基本概念與資料結構表示

首先紅黑樹來個定義：

紅黑樹定義：紅黑樹又稱紅-黑二叉樹，它首先是一顆二叉樹，它具體二叉樹所有的特性。同時紅黑樹更是一顆自平衡的排序二叉樹(平衡二叉樹的一種實現方式)。

我們知道一顆基本的二叉排序樹他們都需要滿足一個基本性質：即樹中的任何節點的值大於它的左子節點，且小於它的右子節點。

按照這個基本性質使得樹的檢索效率大大提高。我們知道在生成二叉排序樹的過程是非常容易失衡的，最壞的情況就是一邊倒（只有右/左子樹），這樣勢必會導致二叉樹的檢索效率大大降低（O(n)），所以為了維持二叉排序樹的平衡，大牛們提出了各種平衡二叉樹的實現演算法，如：AVL，SBT，伸展樹，TREAP ，紅黑樹等等。

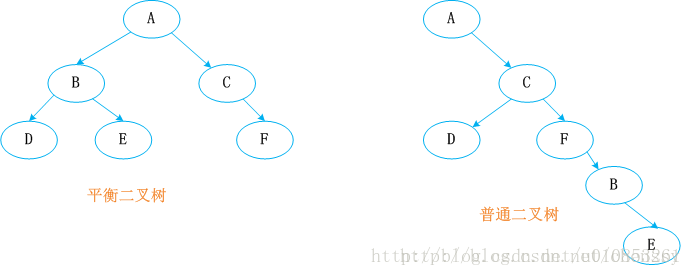
平衡二叉樹必須具備如下特性：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹都是一棵平衡二叉樹。也就是說該二叉樹的任何一個子節點，其左右子樹的高度都相近。下面給出平衡二叉樹的幾個示意圖：

紅黑樹顧名思義就是結點是紅色或者是黑色的平衡二叉樹，它通過顏色的約束來維持著二叉樹的平衡。對於一棵有效的紅黑樹而言我們必須增加如下規則，這也是紅黑樹最重要的5點規則：

1、每個結點都只能是紅色或者黑色中的一種。
2、根結點是黑色的。
3、每個葉結點（NIL節點，空節點）是黑色的。
4、如果一個結點是紅的，則它兩個子節點都是黑的。也就是說在一條路徑上不能出現相鄰的兩個紅色結點。
5、從任一結點到其每個葉子的所有路徑都包含相同數目的黑色結點。

這些約束強制了紅黑樹的關鍵性質: 從根到葉子最長的可能路徑不多於最短的可能路徑的兩倍長。結果是這棵樹大致上是平衡的。因為操作比如插入、刪除和查詢某個值的最壞情況時間都要求與樹的高度成比例，這個在高度上的理論上限允許紅黑樹在最壞情況下都是高效的，而不同於普通的二叉查詢樹。所以紅黑樹它是複雜而高效的，其檢索效率O(lg n)。下圖為一顆典型的紅黑二叉樹：

上面關於紅黑樹的概念基本已經說得很清楚了，下面給出紅黑樹的結點用Java表示資料結構：

private static final boolean RED = true;
private static final boolean BLACK = false
 
;
private Node root;//二叉查詢樹的根節點

//結點資料結構
private class Node{
    private Key key;//鍵
    private Value value;//值
    private Node left, right;//指向子樹的連結:左子樹和右子樹.
    private int N;//以該節點為根的子樹中的結點總數
    boolean color;//由其父結點指向它的連結的顏色也就是結點顏色.

    public Node(Key key, Value value, int N, boolean color) {
        this.key = key;
        this.value = value;
        this.N = N;
        this.color = color;
    }
}

/**
 * 獲取整個二叉查詢樹的大小
 * @return
 */
public int size(){
    return size(root);
}
/**
 * 獲取某一個結點為根結點的二叉查詢樹的大小
 * @param x
 * @return
 */
private int size(Node x){
    if(x == null){
        return 0;
    } else {
        return x.N;
    }
}
private boolean isRed(Node x){
    if(x == null){
        return false;
    }
    return x.color == RED;
}

2.紅黑樹的三個基本操作

紅黑樹在插入，刪除過程中可能會破壞原本的平衡條件導致不滿足紅黑樹的性質，這時候一般情況下要通過左旋、右旋和重新著色這個三個操作來使紅黑樹重新滿足平衡化條件。

旋轉

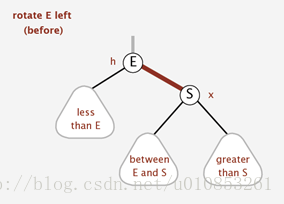
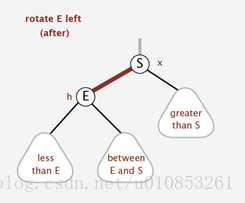
旋轉分為左旋和右旋。在我們實現某些操作中可能會出現紅色右連結或則兩個連續的紅連結，這時候就要通過旋轉修復。

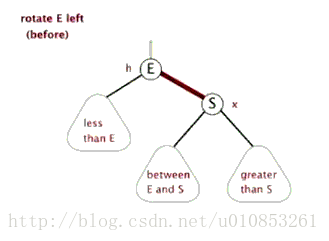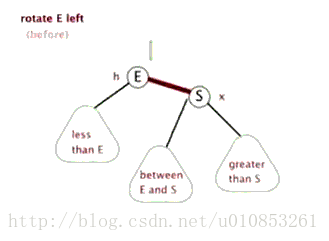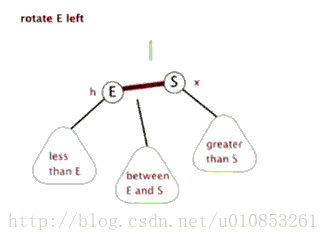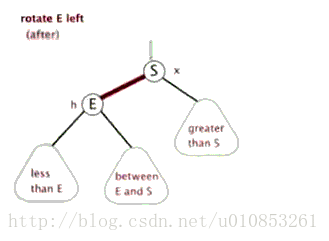
通常左旋操作用於將一個向右傾斜的紅色連結(這個紅色連結鏈連線的兩個結點均是紅色結點)旋轉為向左連結。對比操作前後，可以看出，該操作實際上是將紅線連結的兩個結點中的一個較大的結點移動到根結點上。

左旋的示意圖如下：

左旋的Java實現如下：

/**
 * 左旋轉
 * @param h
 * @return
 */
private Node rotateLeft(Node h){
    Node x = h.right;
    //把x的左結點賦值給h的右結點
    h.right = x.left;
    //把h賦值給x的左結點
    x.left = h;
    //
    x.color = h.color;
    h.color = RED;
    x.N = h.N;
    h.N = 1+ size(h.left) + size(h.right);

    return x;
}

左旋的動畫效果如下：

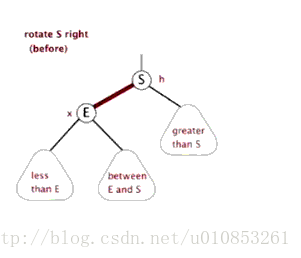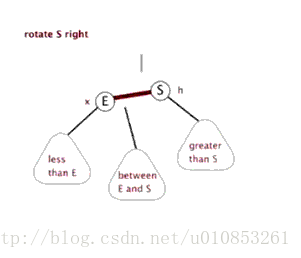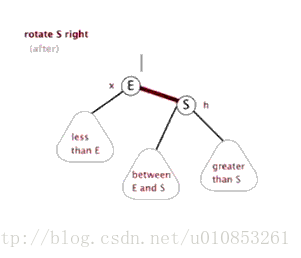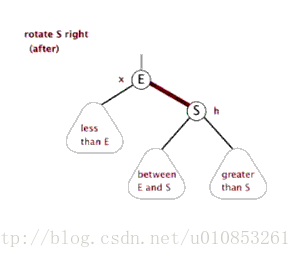
右旋其實就是左旋的逆操作：


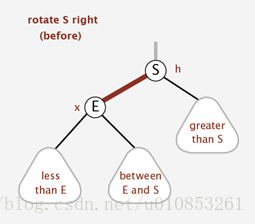
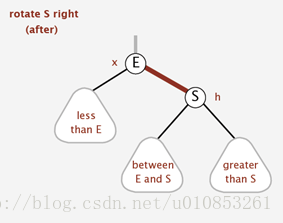
右旋的程式碼如下：

/**
 * 右旋轉
 * @param h
 * @return
 */
private Node rotateRight(Node h){
    Node x = h.left;
    h.left = x.right;
    x.right = h;

    x.color = h.color;
    h.color = RED;
    x.N = h.N;
    h.N = 1+ size(h.left) + size(h.right);
    return x;
}

右旋的動態示意圖：

顏色反轉

當出現一個臨時的4-node的時候，即一個節點的兩個子節點均為紅色，如下圖：

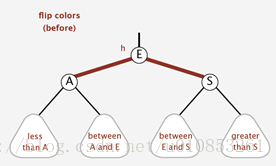
我們需要將E提升至父節點，操作方法很簡單，就是把E對子節點的連線設定為黑色，自己的顏色設定為紅色。顏色反轉之後顏色如下：

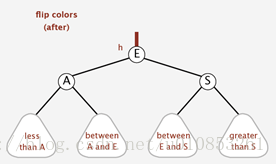
實現程式碼如下：

/**
 * 顏色轉換
 * @param h
 */
private void flipColors(Node h){
    h.color = RED;//父結點顏色變紅
    h.left.color = BLACK;//子結點顏色變黑
    h.right.color = BLACK;//子結點顏色變黑
}

注意：以上的旋轉和顏色反轉操作都是針對單一結點的，反轉或則顏色反轉操作之後可能引起其父結點又不滿足平衡性質。

3. 紅黑樹的插入結點