在看本文之前建議先看一下二叉樹的刪除過程，這裡有一篇文章寫得不錯，可以看一下

1、後繼節點

在看原始碼之前，先說說紅黑樹尋找 待刪除節點t 的 後繼節點 的過程：

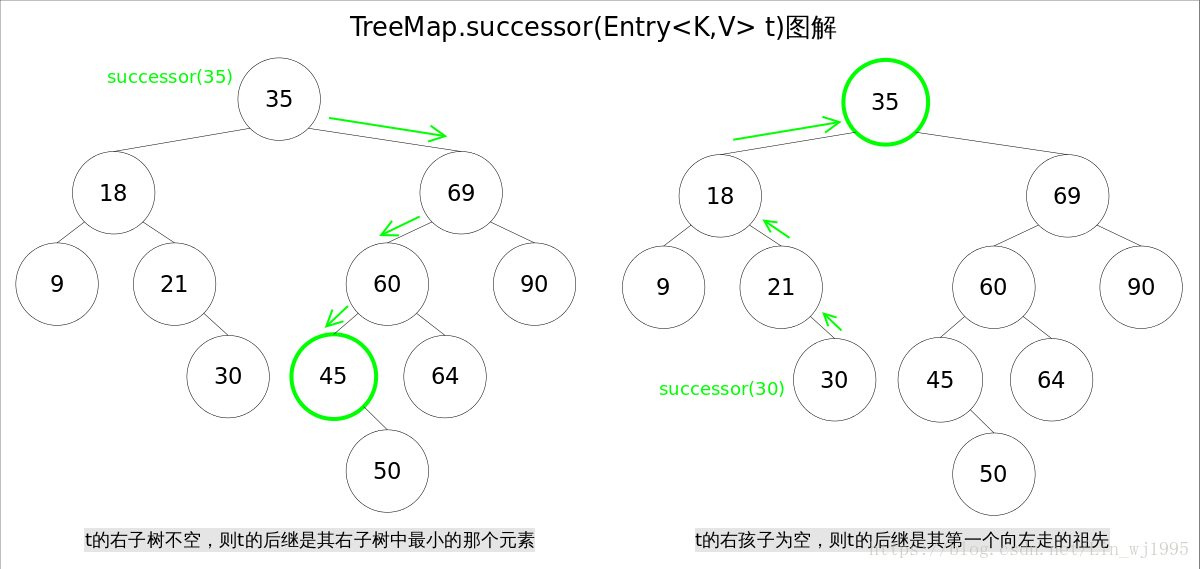
• 如果待刪除節點t有右節點，那麼後繼節點為該節點右子樹中最左的節點，也就是右子樹中值最小的節點
• 如果待刪除節點t無右節點，那麼後繼節點是向上遍歷過程中 第一個向左拐的父節點

圖解過程如下：

注：圖片來源

該過程對應的TreeMap的原始碼如下：

 /**
  * Returns the successor of the specified Entry, or null if no such.
  * 原始碼很好理解就不加註釋了
  */
 

 static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
     if (t == null)
         return null;
     else if (t.right != null) {
         Entry<K,V> p = t.right;
         while (p.left != null)
             p = p.left;
         return p;
     } else {
         Entry<
 
K,V> p = t.parent;
         Entry<K,V> ch = t;
         while (p != null && ch == p.right) {
             ch = p;
             p = p.parent;
         }
         return p;
     }
 }

2、刪除過程

寫一個簡單的單元測試方法：

@Test
public void remove(){
    TreeMap<String, String> map = new
 
 TreeMap();
    map.put("aa","aa");
    map.remove("aa");
}

進入remove方法：

public V remove(Object key) {
    Entry<K,V> p = getEntry(key);
    if (p == null)
        return null;

    V oldValue = p.value;
    deleteEntry(p);
    return oldValue;
}

點選進入deleteEntry（核心操作）方法：

/**
 * 刪掉p節點，然後對TreeMap進行rebalance
 * 英文的註釋都是官方的註釋
 */
private void deleteEntry(Entry<K,V> p) {
	modCount++;	//記錄修改次數
	size--;	//size減1

	// If strictly internal, copy successor's element to p and then make p
	// point to successor.
	if (p.left != null && p.right != null) {//如果待刪除的節點p左右節點都有
		Entry<K,V> s = successor(p);//得到p的後繼節點，注意，根據前面我們對後繼節點的瞭解後知道，
									//該操作得到的肯定是p的右子樹的最左節點！
		p.key = s.key;		//這裡對key、value的設定看似很普通，其實很關鍵。該操作實際上已經把p節點刪除掉了，但是注意顏色沒有改變
		p.value = s.value;	
		p = s;	//然後把後繼節點的指標賦值給p，注意，這時修改p的指標是沒有問題的，因為經過上面的操作已經把節點刪掉了
	} // p has 2 children

	//下面的p節點要不就只有左節點、要不就只有右節點、要不就沒有子節點
	//因為有左右節點的p經過上面的操作後已經指向了後繼節點，這裡的後繼節點一定是沒有左節點的	
	//如果p有經過上面操作，那麼實際上已經把需要刪除的節點已經刪除了，而且經過操作後需要刪除的節點上的key、value已經變成了後繼節點的key、value。
	//操作後的p已經指向了後繼節點，也就是說現在的p引用的node跟需要刪除的node的key和value是一樣的。所以該p指向的node也是要刪除的，
	//經過上面的方法就把刪除過程轉換成下面統一的操作

	// Start fixup at replacement node, if it exists.
	Entry<K,V> replacement = (p.left != null ? p.left : p.right);

	if (replacement != null) {
		// Link replacement to parent
		replacement.parent = p.parent;
		if (p.parent == null)
			root = replacement;
		else if (p == p.parent.left)
			p.parent.left  = replacement;
		else
			p.parent.right = replacement;

		// Null out links so they are OK to use by fixAfterDeletion.
		p.left = p.right = p.parent = null;

		// Fix replacement
		if (p.color == BLACK) //只有node為黑色時tree才需要fix
			fixAfterDeletion(replacement);
	} else if (p.parent == null) { // return if we are the only node.
		root = null;
	} else { //  No children. Use self as phantom replacement and unlink.
		if (p.color == BLACK)	//只有node為黑色時tree才需要fix
			fixAfterDeletion(p);

		if (p.parent != null) {
			if (p == p.parent.left)
				p.parent.left = null;
			else if (p == p.parent.right)
				p.parent.right = null;
			p.parent = null;
		}
	}
}

最後就是fixAfterDeletion方法了，這個方法總結起來就是如下操作：
針對的節點：當前節點x、父節點p、兄弟節點sib、兄弟節點的左子節點ch_l、兄弟節點的右子節點ch_r，如果滿足一定情況就進行左旋或者右旋、改色，最後fix完成。

3、討論

在文章最後來說一下我學習紅黑樹之前的疑惑：為什麼已經有了二叉樹和平衡二叉樹，還需要紅黑樹？紅黑樹有什麼優點？
我的個人看法是：
普通二叉樹插入很快，但是如果樹節點很多，那麼就很容易造成樹的“傾斜”，就是樹的左節點很深，而右節點很淺。這樣查詢節點時跟連結串列查詢的時間複雜度就差別不大。也就是說普通二叉樹適合對於插入效能要求很高而基本不怎麼查詢的場景。
平衡二叉樹則有點跟普通二叉樹相反，它可以時時刻刻保持左右子樹的平衡，這樣對於查詢就很友好。但是對於插入操作就不是很友好，每次插入很大概率會觸發樹的rebalance，影響插入效能（當然，這個效能是相對的，對於指標的修改操作是很快的）。
於是乎紅黑樹出現了，一種兼顧於插入和查詢的樹，插入時不會為了時時刻刻保持平衡而進行rebalance，也不會讓左右子樹的高度差非常大~

如果有更好的想法，可以交流討論哈~~