0、文章結構

文章的行文邏輯如下，看官可以根據需要跳讀，節省時間。

1、介紹underflow和underflow.

2、問題起源

3、問起探索

4、underflow和underflow的常見情形

5、處理一些溢位問題的小技巧

6、對其中的小技巧的優缺點的比較

1、什麼是underflow和overflow

通俗來講，在計算機中浮點數都是離散的，有限的。因此計算機無法用有限的浮點數來表示無限的實數。在用浮點數表示實數時，很多數都會存在近似誤差。其中一種是下溢（underflow）。比如，一個非常接近於零的數值A（實際上A>0），計算機會直接把該數值判為零，雖然實際上它並不為零。另一種數值誤差是上溢（overflow），通俗而言，當一個數值a非常接近某一計算機表示的數值b時（實際a<b），計算機用b表示a。

2、起源-算術編碼（arithmetic coding）作業初識underflow

音訊老師佈置一個作業，要求寫一段程式實現算術編碼，被編碼的字串為：ALIALIBABA。

這個很簡單，很快就用matlab寫出來了，最終和老師給的答案一樣。

接著老師就佈置了第二個算術編碼的作業，實現對下方字串的編碼，包含空格。

DIGITAL AUDIO TECHNOLOGY AND APPLICATION

程式碼中輸入該字串，可是range輸出值為0。

理論上來講，range是一個非常非常小的值，但不等於零。

這時，突然意識到，老師上課時講到的，程式在數值運算中出現underflow。

3、關於underflow問題的探索

變數Range被計算機判為零，但是它實際上並不等於零。

那麼在matlab中，數值小於多少會被計算機判為零呢？

EPS函式

EPS是MATLAB中的函式，表示浮點相對精度。 對雙精度數值來說eps表示從 1.0 到下一個最大雙精度數的距離。對單精度數值來說eps表示從 1.0 到下一個最大單精度數的距離。

在command window中輸入：help eps

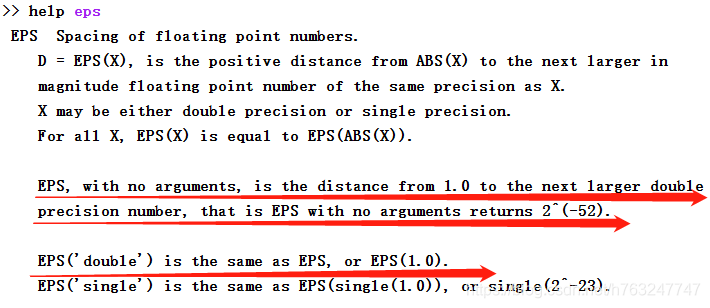
Matlab中變數預設為double型別，所以其判別值為2^(-52)，相當於

所以當變數值小於2.22e（-16）時，計算機會直接判為零，這時就需要考慮underflow了。

4、常見數值誤差的情形

由此引出另外一個問題：哪些情況會出現數值誤差（underflow 或者overflow）？

論壇裡有非常多大佬的精彩留言，讓人豁然開朗。

情形1-underflow

計算所得0.4的實際值小於0.4。

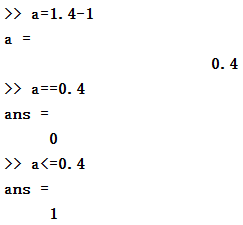
情形2-由underflow出現的錯誤

計算機中的計算值為3，並不等於4。

情形2-誤差精度

控制檯輸出，可以發現誤差越來越大。

對於情景2問題的分析

雙精度浮點數在計算機中使用科學計數法儲存，下圖所示浮點數格式。

兩個浮點數相減時，會存在有效位數字的誤差。

假如1.4-1在計算機中的表示為0.3999….9*e(0)(13個9)。

100000000.4-100000000=(1.000000004-1.00000000)*e(8)=0. 0000000039..9(5個9)*e(8)。

運算精度就變差了，誤差也會增大。

情形3-overflow

情形4-由於overflow出現的程式碼錯誤

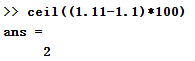
4、處理一些溢位問題的小技巧

4.1、判斷兩個數是否相等

可以使用如下公式：

abs(a-b) < eps(a) or eps(b)

如果不等式成立，則a,b相等。

4.2、解決underflow問題

比如floor((1.4-1)*10)，matlab執行的結果為3，並不等於4。為了得到正確的程式碼，可以如下改寫程式碼。overflow的問題也可以使用類似思路。

4.3、提高精度

a-b的結果小於eps(0)時，為了避免結果被計算機判為零，可以使用其它工具，比如advanpix提高精度，比如精確到小數點後200位。

4.4、移位

比如計算0.0000000000111-0.0000000000101時，可以先都乘以10^10，再相減，然後差值再除以10^10，這樣可以提高計算精度。

5、提高精度和移位的比較

方法2可以更快的解決matlab中出現的溢位問題，但是方法3更加實用。因為在工程領域，很難找到類似advanpix的工具。比如老闆要求在arm晶片上實現對音訊的算術編碼，這樣只能用方法3了。