【轉】字尾自動機
小Hi:今天我們來學習一個強大的字串處理工具:字尾自動機(Suffix Automaton,簡稱SAM)。對於一個字串S,它對應的字尾自動機是一個最小的確定有限狀態自動機(DFA),接受且只接受S的字尾。
小Hi:比如對於字串S="aabbabd",它的字尾自動機是:
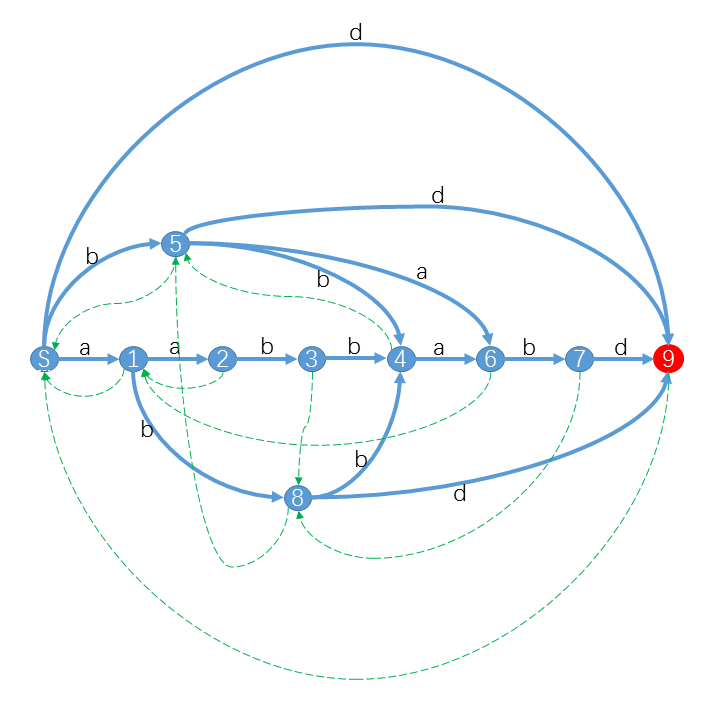
其中紅色狀態是終結狀態。你可以發現對於S的字尾,我們都可以從S出發沿著字元標示的路徑(藍色實線)轉移,最終到達終結狀態。例如"bd"對應的路徑是S59,"abd"對應的路徑是S189,"abbabd"對應的路徑是S184679。而對於不是S字尾的字串,你會發現從S出發,最後會到達非終結狀態或者“無路可走”。特別的,對於S的子串,最終會到達一個合法狀態。例如"abba"路徑是S1846,"bbab"路徑是S5467。而對於其他不是S子串的字串,最終會“無路可走”。 例如"aba"對應S18X,"aaba"對應S123X。(X表示沒有轉移匹配該字元)
小Ho:好像很厲害的樣子!對於任意字串都能構造出一個SAM嗎?另外圖中那些綠色虛線是什麼?
小Hi:是的,任意字串都能構造出一個SAM。我們知道SAM本質上是一個DFA,DFA可以用一個五元組 <字符集,狀態集,轉移函式、起始狀態、終結狀態集>來表示。下面我們將依次介紹對於一個給定的字串S如何確定它對應的 狀態集 和 轉移函式 。至於那些綠色虛線雖然不是DFA的一部分,卻是SAM的重要部分,有了這些連結SAM是如虎添翼,我們後面再細講。
SAM的States
小Hi:這一節我們將介紹給定一個字串S,如何確定S對應的SAM有哪些狀態。首先我們先介紹一個概念 子串的結束位置集合 endpos。對於S的一個子串s,endpos(s) = s在S中所有出現的結束位置集合。還是以S="aabbabd"為例,endpos("ab") = {3, 6},因為"ab"一共出現了2次,結束位置分別是3和6。同理endpos("a") = {1, 2, 5}, endpos("abba") = {5}。
小Hi:我們把S的所有子串的endpos都求出來。如果兩個子串的endpos相等,就把這兩個子串歸為一類。最終這些endpos的等價類就構成的SAM的狀態集合。例如對於S="aabbabd":
| 狀態 | 子串 | endpos |
|---|---|---|
| S | 空串 | {0,1,2,3,4,5,6} |
| 1 | a | {1,2,5} |
| 2 | aa | {2} |
| 3 | aab | {3} |
| 4 | aabb,abb,bb | {4} |
| 5 | b | {3,4,6} |
| 6 | aabba,abba,bba,ba | {5} |
| 7 | aabbab,abbab,bbab,bab | {6} |
| 8 | ab | {3,6} |
| 9 | aabbabd,abbabd,bbabd,babd,abd,bd,d | {7} |
小Ho:這些狀態恰好就是上面SAM圖中的狀態。
小Hi:沒錯。此外,這些狀態還有一些美妙的性質,且等我一一道來。首先對於S的兩個子串s1和s2,不妨設length(s1) <= length(s2),那麼 s1是s2的字尾當且僅當endpos(s1) ⊇ endpos(s2),s1不是s2的字尾當且僅當endpos(s1) ∩ endpos(s2) = ∅。
小Ho:我驗證一下啊... 比如"ab"是"aabbab"的字尾,而endpos("ab")={3,6},endpos("aabbab")={6},是成立的。"b"是"ab"的字尾,endpos("b")={3,4,6}, endpos("ab")={3,6}也是成立的。"ab"不是"abb"的字尾,endpos("ab")={3,6},endpos("abb")={4},兩者沒有交集也是成立的。怎麼證明呢?
小Hi:證明還是比較直觀的。首先證明s1是s2的字尾=>endpos(s1) ⊇ endpos(s2):既然s1是s2字尾,所以每次s2出現時s1以必然伴隨出現,所以有endpos(s1) ⊇ endpos(s2)。再證明endpos(s1) ⊇ endpos(s2)=>s1是s2的字尾:我們知道對於S的子串s2,endpos(s2)不會是空集,所以endpos(s1) ⊇ endpos(s2)=>存在結束位置x使得s1結束於x,並且s2也結束於x,又length(s1) <= length(s2),所以s1是s2的字尾。綜上我們可知s1是s2的字尾當且僅當endpos(s1) ⊇ endpos(s2)。s1不是s2的字尾當且僅當endpos(s1) ∩ endpos(s2) = ∅是一個簡單的推論,不再贅述。
小Ho:我好像對SAM的狀態有一些認識了!我剛才看上面的表格就覺得SAM的一個狀態裡包含的子串好像有規律。考慮到SAM中的一個狀態包含的子串都具有相同的endpos,那它們應該都互為字尾?
小Hi:你觀察力還挺敏銳的。下面我們就來講講一個狀態包含的子串究竟有什麼關係。上文提到我們把S的所有子串按endpos分類,每一類就代表一個狀態,所以我們可以認為一個狀態包含了若干個子串。我們用substrings(st)表示狀態st中包含的所有子串的集合,longest(st)表示st包含的最長的子串,shortest(st)表示st包含的最短的子串。例如對於狀態7,substring(7)={aabbab,abbab,bbab,bab},longest(7)=aabbab,shortest(7)=bab。
小Hi:對於一個狀態st,以及任意s∈substrings(st),都有s是longest(st)的字尾。證明比較容易,因為endpos(s)=endpos(longest(st)),所以endpos(s) ⊇ endpos(longest(st)),根據我們剛才證明的結論有s是longest(st)的字尾。
小Hi:此外,對於一個狀態st,以及任意的longest(st)的字尾s,如果s的長度滿足:length(shortest(st)) <= length(s) <= length(longsest(st)),那麼s∈substrings(st)。 證明也是比較容易,因為:length(shortest(st)) <= length(s) <= length(longsest(st)),所以endpos(shortest(st)) ⊇ endpos(s) ⊇ endpos(longest(st)), 又endpos(shortest(st)) = endpos(longest(st)),所以endpos(shortest(st)) = endpos(s) = endpos(longest(st)),所以s∈substrings(st)。
小Ho:這麼說來,substrings(st)包含的是longest(st)的一系列連續後綴?
小Hi:沒錯。比如你看狀態7中包含的就是aabbab的長度分別是6,5,4,3的字尾;狀態6包含的是aabba的長度分別是5,4,3,2的字尾。
SAM的Suffix Links
小Hi:前面我們講到substrings(st)包含的是longest(st)的一系列連續後綴。這連續的字尾在某個地方會“斷掉”。比如狀態7,包含的子串依次是aabbab,abbab,bbab,bab。按照連續的規律下一個子串應該是"ab",但是"ab"沒在狀態7裡,你能想到這是為什麼麼?
小Ho:aabbab,abbab,bbab,bab的endpos都是{6},下一個"ab"當然也在結束位置6出現過,但是"ab"還在結束位置3出現過,所以"ab"比aabbab,abbab,bbab,bab出現次數更多,於是就被分配到一個新的狀態中了。
小Hi:沒錯,當longest(st)的某個字尾s在新的位置出現時,就會“斷掉”,s會屬於新的狀態。比如上例中"ab"就屬於狀態8,endpos("ab"}={3,6}。當我們進一步考慮"ab"的下一個字尾"b"時,也會遇到相同的情況:"b"還在新的位置4出現過,所以endpos("b")={3,4,6},b屬於狀態5。在接下去處理"b"的字尾我們會遇到空串,endpos("")={0,1,2,3,4,5,6},狀態是起始狀態S。
小Hi:於是我們可以發現一條狀態序列:7->8->5->S。這個序列的意義是longest(7)即aabbab的字尾依次在狀態7、8、5、S中。我們用Suffix Link這一串狀態連結起來,這條link就是上圖中的綠色虛線。
小Ho:原來如此。
小Hi:Suffix Links後面會有妙用,我們暫且按下不表。
SAM的Transition Function
小Hi:最後我們來介紹SAM的轉移函式。對於一個狀態st,我們首先找到從它開始下一個遇到的字元可能是哪些。我們將st遇到的下一個字元集合記作next(st),有next(st) = {S[i+1] | i ∈ endpos(st)}。例如next(S)={S[1], S[2], S[3], S[4], S[5], S[6], S[7]}={a, b, d},next(8)={S[4], S[7]}={b, d}。
小Hi:對於一個狀態st來說和一個next(st)中的字元c,你會發現substrings(st)中的所有子串後面接上一個字元c之後,新的子串仍然都屬於同一個狀態。比如對於狀態4,next(4)={a},aabb,abb,bb後面接上字元a得到aabba,abba,bba,這些子串都屬於狀態6。
小Hi:所以我們對於一個狀態st和一個字元c∈next(st),可以定義轉移函式trans(st, c) = x | longest(st) + c ∈ substrings(x) 。換句話說,我們在longest(st)(隨便哪個子串都會得到相同的結果)後面接上一個字元c得到一個新的子串s,找到包含s的狀態x,那麼trans(st, c)就等於x。
小Ho:吼~ 終於把SAM中各個部分搞明白了。
小Hi:SAM的構造有時空複雜度均為O(length(S))的演算法,我們將在後面介紹。這一期你可以先用暴力演算法依照定義構造SAM,先對SAM有個直觀認識再說。
小Ho:沒問題,暴力演算法我最拿手了。我先寫程式去了。
