Dijkstra演算法是由荷蘭電腦科學家狄克斯特拉於1959 年提出的，因此又叫狄克斯特拉演算法。是從一個頂點到其餘各頂點的最短路徑演算法，解決的是有向圖中最短路徑問題。迪傑斯特拉演算法主要特點是以起始點為中心向外層層擴充套件，直到擴充套件到終點為止。

      下面，我用python來舉例詳細介紹這個演算法

     問題如下：

                    如圖所示（我們規定箭頭上的數字為時間）現有如下路徑圖，我們想盡快從起點到達終點，那也就是求最快路徑的問題了

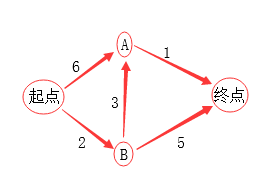
接下來我們先把問題建模

這是GRAPH表，將該路徑描述用表格形式表現出來

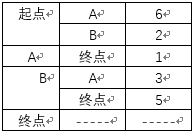
graph = {}#定義鄰居表
graph["start"] = {}#起點的鄰居
graph["start"]["a"] = 6
graph["start"]["b"] = 2

graph["a"] = {}#a點的鄰居
graph["a"]["end"] = 1

graph["b"] = {}#b點的鄰居
graph["b"]["a"] = 3
graph["b"]["end"] = 5

graph["end"] = {}#終點沒有任何鄰居
 

然後是COSTS表，用於將起點到各個點的的開銷列出來，不能直接到達的，該事件設為無窮大（用“-”表示，後期再更改）

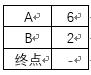
costs = {}#定義開銷表,即起點到其餘節點的開銷，不是直接到達的，就暫時用無窮大定義
costs["a"] = 6
costs["b"] = 2
costs["end"] = float("inf")#定義極大值

最後是PARENT表，用於記錄每個節點的父節點（父節點：如B被起點指向，則稱起點是B的父節點）（若有某個遠端節點（非起點指向）被兩個節點指向，則暫時不寫，用“-”表示）

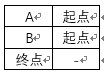
parent = {}#定義父節點表，僅看只有一個父節點的節點，若有兩個父節點，則暫時定義為空
parent["a"] = "start"
parent["b"] = "start"
parent["end"] = None #終點節點（非遠端節點）在表中有兩個父節點，故暫時不填
 

至此，問題描述，建模完畢

我們先定義一個列表，用於儲存那些被處理的節點，防止重複處理

processed = [] #定義flag，用於標記某節點已被處理，防止多餘計算甚至死迴圈

接下來是具體演算法描述部分：

定義find_lowest_cost_node函式，傳入COSTS表，用於查詢當前未處理的，函式返回用時最少的下一節點，通俗點來說，就是把起點的子節點按用時情況，從小到達依次返回一個子節點（是返回一個節點，不是時間），思想是：每次定義一個無窮大，然後每次將起點的子節點遍歷，直到找出此時的用時最小的節點，思想類似氣泡排序中的找出最大/小值

#此函式的作用是依次獲取該起點能到的所有點，從小到大
def find_lowest_cost_node(costs):#找出到達開銷最小的節點
    lowest_cost = float("inf")#定義極大值
    lowest_cost_node = None
    for node in costs:
        cost = costs[node]
        if cost < lowest_cost and node not in processed:
            lowest_cost = cost
            lowest_cost_node = node
    return lowest_cost_node
 

 最關鍵的下面的演算法思想：

上一個函式將依次返回起點到另一個用時最少的節點，然後分如下幾步：

         1.記錄起點到該點的用時cost

         2.遍歷該節點的所有鄰居，分別得到該點到其各個鄰居的用時（比如B的一個鄰居A）

         3.在原始costs表中查詢到起點到A的開銷為6，就是程式碼中的costs[n]，起點到B的開銷為2（也就是步驟1中cost）B到A的開銷為3,就是程式碼中的neighbirs[n]，將costs[A]與cost+neighbirs[A]作比較，也就是（6與2+3作比較），後者小於前者，那麼就更新路徑（之前是起點直接到A，用時6，現在要想到達A，就起點先到B，然後B再到A，用時5，顯然後面這條路徑用時少一些，然後更新costs表和parent表）

def main():
    node = find_lowest_cost_node(costs)
    while node is not None:
        cost = costs[node]
        neighbors = graph[node]#獲取該node節點的鄰居
        for n in neighbors.keys():#將該節點的鄰居依次遍歷出來
            new_cost = cost+neighbors[n]#計算從當前節點到達其鄰居的開銷與其起點到其開銷的和
            if costs[n] > new_cost:#如果新開銷和比之前的開銷小，就更新開銷表和父節點表
                costs[n] = new_cost#將起點到該節點的開銷更新
                parent[n] = node#更新該節點的父節點，意味著從這條路徑過來花的時間最少
        processed.append(node)#將該節點標記為已處理節點
        node = find_lowest_cost_node(costs)#繼續找下一個未被處理的節點
    print(costs["end"])