十二、圖的演算法入門--(4)最短路問題---Dijkstra演算法實現
先來看這樣一個問題:有n座城市,已知任意兩個座城市之間的距離,現在要分別求出城市A到其他n-1座城市的最短路徑,
也就是求所經過的距離和的最小值。
這是一個經典的單源最短路問題,即求一起點到其餘各個頂點的最短路徑問題。
首先,我們可以把該場景看成是一個帶權圖,把n個城市看成n個頂點,把兩座城市之間的距離看成是兩個頂點之間的邊權值,
這樣問題就轉化成了求頂點A到其餘n-1個頂點的最短路徑。
Dijkstra演算法是最常見的求解單源最短路問題的演算法。
先來看看 Dijkstra 演算法的具體過程:
定義帶權圖 G 所有頂點的集合為 V,接著我們再定義已確定最短路徑的頂點集合為 U,初始集合
-
首先我們將起點 x 加入集合 U,並在陣列 A 中記錄起點 x 到各個點的最短路徑(如果頂點到起點 x 有直接相連的邊,則最短路徑為邊權值,否則為一個極大值)。
-
從陣列 A 中選擇一個距離起點 x 最近的、且不屬於集合 U 的頂點 v(如果有多個頂點 v,任選其一即可),將頂點 v 加入集合 U,並更新所有與頂點 v 相連的頂點到起點x 的最短路徑。
-
重複第二步操作,直至集合 U 等於集合 V。
演算法結束,陣列 A 記錄了起點 x 到其餘 n−1 個點的最短路徑。
下面我們用一個小例子來模擬下 Dijkstra 演算法吧。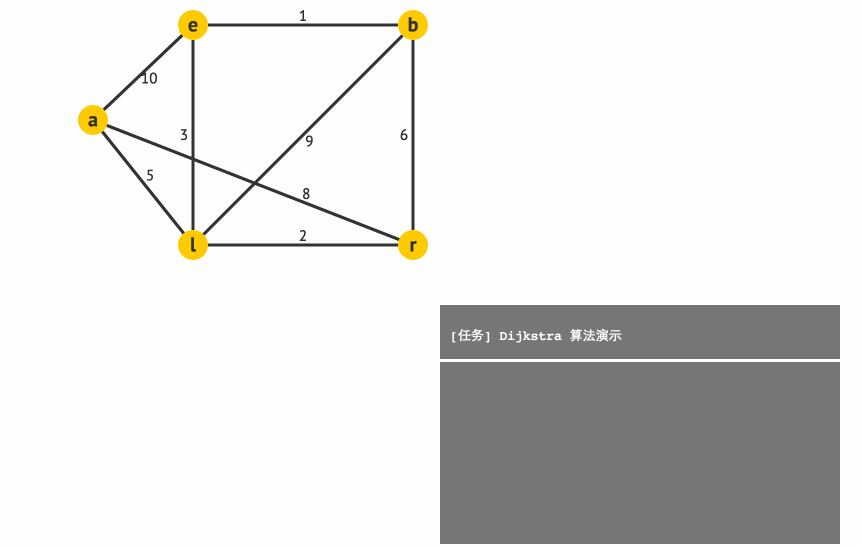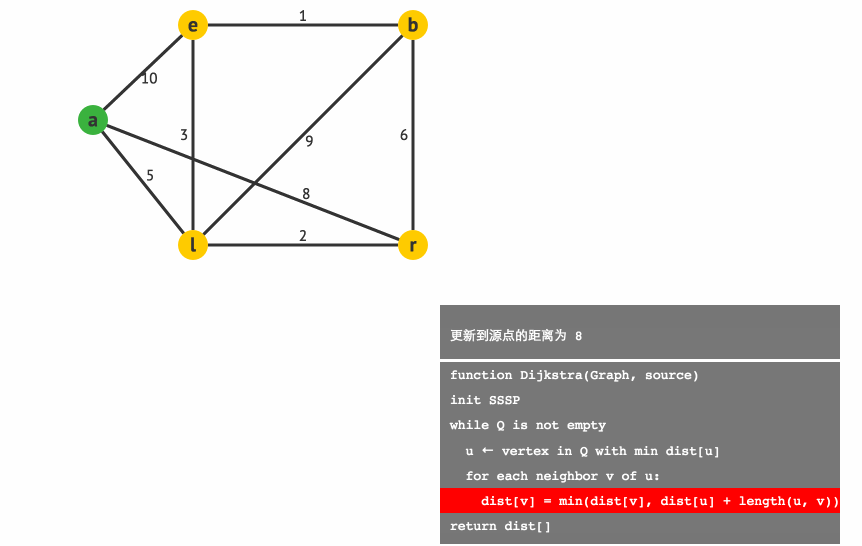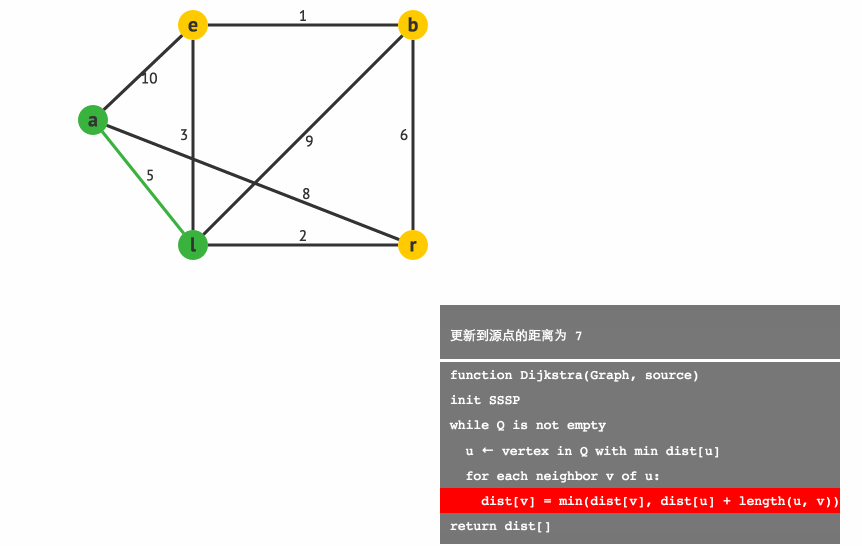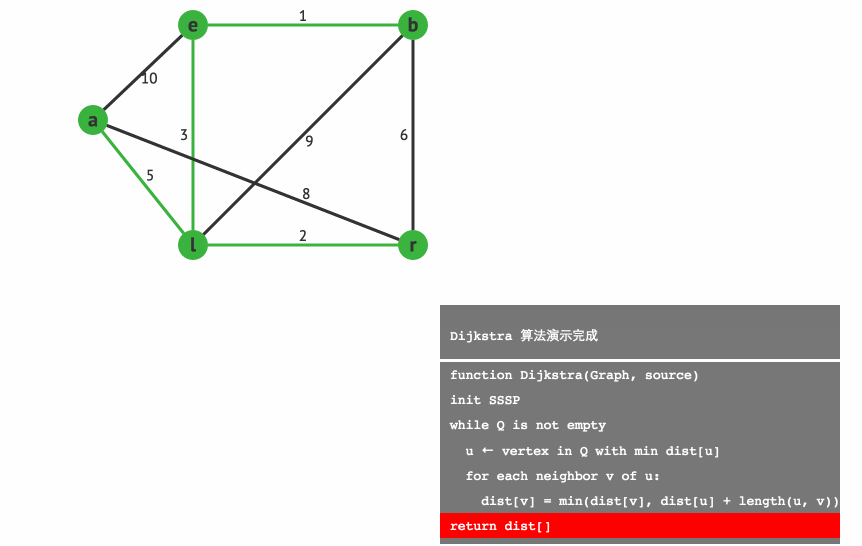
通過模擬,最終我們可以得到起點 a 到各點的最短路徑分別為:
l:5(a−>l)
e:8(a−>l−>e)
r:7(a−>l−>r)
b:9(a−>l−>e−>b)
仔細分析演算法,我們可以發現,Dijkstra 演算法和前面講解的 Prim 演算法很相像,都是從一個點開始,每次確定一個點並完成更新,重複操作直至 n 個點都確定為止。Dijkstra
演算法的時間複雜度為
需要注意的是,Dijkstra 不適用於有邊權為負數的情況哦,否則會影響演算法的正確性。
演算法實現:計算一個帶權無向圖中從頂點0出發,到所有頂點的最短路徑長度。
比如下圖:
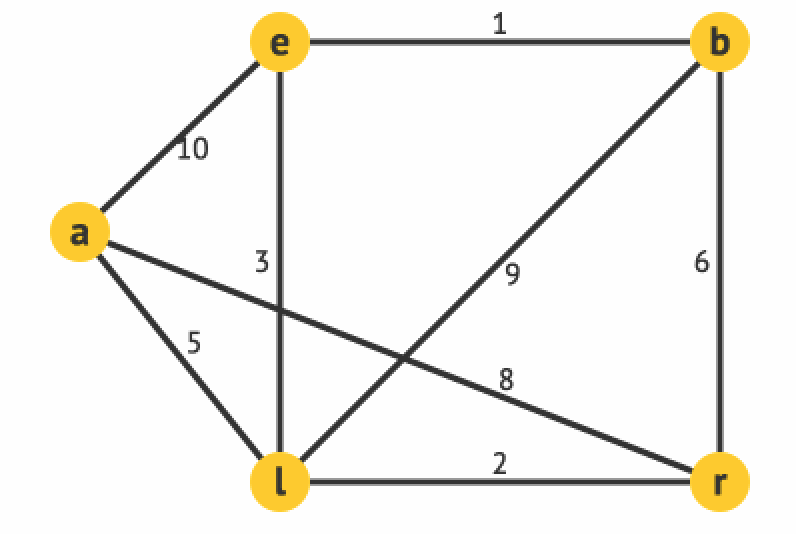
在這個圖中,從a出發到e的最短路a->l->e,長度是8;到b的最短路是a->l->e->b,長度為9;
程式碼如下:
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const int INF = 0x3f3f3f3f;
struct Edge {
int vertex, weight;
};
class Graph {
private:
int n;
vector<Edge> * edges;
bool * visited;
public:
int * dist;
Graph (int input_n) {
n = input_n;
edges = new vector<Edge>[n];
dist = new int[n];
visited = new bool[n];
memset(visited, 0, n);
memset(dist, 0x3f, n * sizeof(int));
}
~Graph() {
delete[] dist;
delete[] edges;
delete[] visited;
}
void insert(int x, int y, int weight) {
edges[x].push_back(Edge{y, weight});
edges[y].push_back(Edge{x, weight});
}
void dijkstra(int v) {
//[1]初始化
dist[v] = 0;
//[2]n次迴圈,每次找出從源點出發最短路徑最小的未訪問的頂點,標記為已訪問,之後更新
//和這個頂點相鄰的所有頂點的最短路。
for(int i=0; i<n; i++) {
int min_dist = INF, min_vertex;
//[3]找出所有未訪問頂點中從源點出發最短路徑最小的,並將其儲存。
for(int j=0; j<n; ++j) {
//[4]如果頂點j未訪問且最短路徑比min_dist記錄的更小,那麼就用源點到頂點j的最短路徑更新
//min_dist,然後將頂點編號儲存到min_vertex中。
if(!visited[j] && dist[j] < min_dist) {
min_dist = dist[j];
min_vertex = j;
}
}
//[5]將min_vertex點的訪問標誌置為1
visited[min_vertex] = 1;
//[6]鬆弛操作:對於已經找到的當前最近頂點min_vertex,如果源點到它的最短路徑長度
//min_dist加上和min_vertex相鄰邊的邊權小於源點到該邊另一端的最短路徑,那麼就
//更新另一端的最短路徑,也就是dist陣列中對應的值。
for(Edge &j:edges[min_vertex]) {
if(min_dist+j.weight < dist[j.vertex]) {
dist[j.vertex] = min_dist + j.weight;
}
}
}
}
};
int main() {
int n, m;
cin >> n >> m;
Graph g(n);
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
g.insert(a, b, c);
}
g.dijkstra(0);
for (int i = 0; i < n; i++) {
cout << i << ": " << g.dist[i] << endl;
}
return 0;
}