前面在討論兩個不同座標系之間的轉換時都是通過尤拉旋轉或者四元素來定義的。今天直接給出方向餘弦陣的定義和用途。

方向餘弦的定義

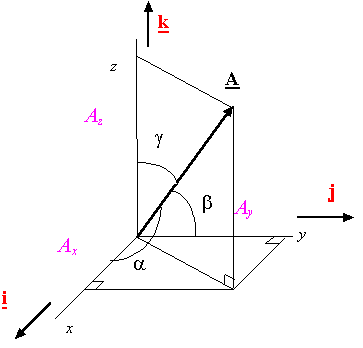
方向餘弦是指在解析幾何裡，一個向量的三個方向餘弦分別是這向量與三個座標軸之間的角度的餘弦。 如下圖中，向量A與座標系三個軸$i,j,k$的夾角為$\alpha,\beta,\gamma$,則向量A的方向餘弦就是： $[\cos(\alpha),\cos(\beta),\cos(\gamma)]$

方向餘弦矩陣

方向餘弦矩陣是由兩組不同的標準正交基的基底向量之間的方向餘弦所形成的矩陣。方向餘弦矩陣可以用來表達一組標準正交基與另一組標準正交基之間的關係。 使用$i_{}$

將$i_b,j_b,k_b$分別在座標系$ox_iy_iz_i$的方向餘弦組成矩陣$M$(注意，按列組成)： $M=\begin{bmatrix} i_b\cdot i_i &j_b\cdot i_i &k_b\cdot i_i\\ i_b\cdot j_i &j_b\cdot j_i &k_b\cdot j_i\\ i_b\cdot k_i &j_b\cdot k_i &k_b\cdot k_i \end{bmatrix} \qquad(2)$