名詞解釋 

樹這個資料結構用到了遞迴的概念：樹的子樹還是樹；

度：節點的子樹個數；

樹的度：樹中任意節點的度的最大值；

兄弟：兩節點的parent相同；

層：根在第一層，以此類推；

高度：葉子節點的高度為1，根節點高度最高；

有序樹：樹中各個節點是有次序的；

森林：多個樹組成；

樹的表示法

1.雙親表示法：每個節點儲存：資料、parent在陣列中的下標；

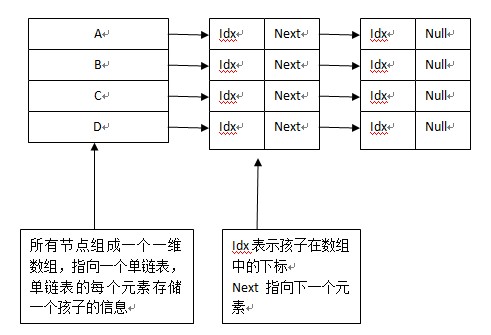
2.孩子表示法：全部節點組成一個數組，每個陣列指向一個單鏈表，存放其孩子；如下圖：

3.雙親孩子表示法

4.孩子兄弟表示法

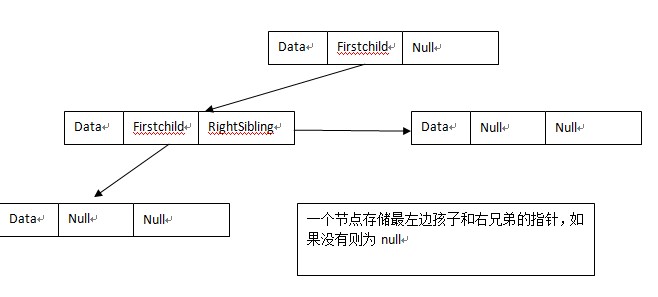
此種方法的好處在於一個多叉樹能夠轉換成一顆二叉樹，是樹轉換成二叉樹的好辦法；

線性表是樹的特殊情況；

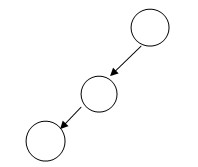
斜樹：所有節點只有左節點或右節點；比如：

滿二叉樹

完全二叉樹：從左到右、從上到下構建的二叉樹；比如：

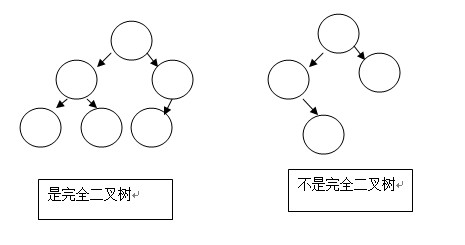
性質

1.第i層至多有個節點；

2.深度為k的樹最多有2^k -1個節點；

3.任意二叉樹，度為0的節點數=度為2的節點數+1；

4.如果i為父親的編號，則孩子的編號為2i和2i+1;

5.如果孩子的編號為k,則父親的編號為floor(k/2);

二叉樹的儲存結構

(1)順序儲存：只適用於完全二叉樹；

(2)鏈式儲存：最通用的儲存方法；

但是這樣很浪費空間，因為會有很多空指標（如果有n個節點，則有2n個left、right指標，但是用到的只有n-1個指標）

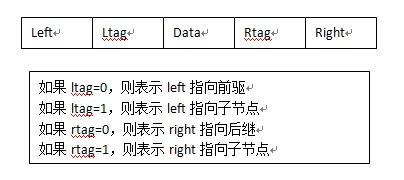
改進：線索二叉樹：將空指標連結到前驅或後繼節點；（此處前驅和後繼是按照中序遍歷上講的）

節點資料結構如下圖：

比如：

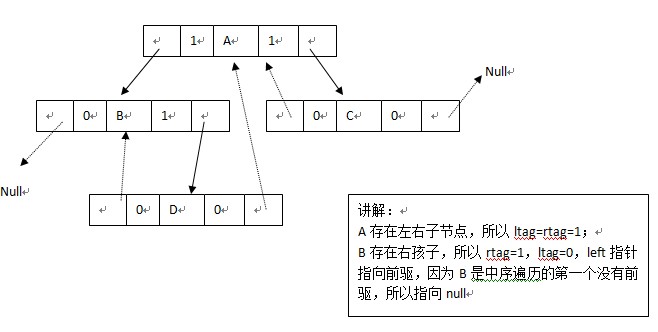
一般構造線索二叉樹的過程步驟如下：

(1)構造一般二叉樹；

(2)遍歷二叉樹的同時，建立線索二叉樹；

二叉樹的遍歷

(1)前序遍歷：先雙親、再左孩子、最後右孩子；

(2)中序遍歷：先左孩子、再雙親、最後右孩子；

(3)後序遍歷：先左孩子、再右孩子、最後雙親；

(4)層次遍歷：一層一層，從左到右、從上到下遍歷；

注意：

(1)已知前序、後序遍歷結果，不能推匯出一棵確定的樹；

(2)已知前序、中序遍歷結果，能夠推匯出後序遍歷結果；

(2)已知後序、中序遍歷結果，能夠推匯出前序遍歷結果；

擴充套件二叉樹

對於一般二叉樹的擴充，為了能夠通過一個遍歷序列建立二叉樹，擴充套件二叉樹如圖所示：

如果存在遍歷序列：AB##C##,則可以很容易的建立二叉樹；

此種方式很方便，因為一般來說都需要三種遍歷方式中的兩種才可以確定一個二叉樹；

樹、森林、二叉樹的轉換

樹-->二叉樹

根據兄弟孩子表示法進行轉換；

森林-->二叉樹

 二叉樹-->樹

 二叉樹-->森林

Huffman編碼

Huffman是一種字首編碼；

Huffman編碼是建立在Huffman樹的基礎上進行的，因此為了進行Huffman編碼，必須先構建Huffman樹；

樹的路徑長度是每個葉節點到根節點的路徑之和；

帶權路徑長度是（每個葉節點的路徑長度*wi）之和；

Huffman樹是最小帶權路徑長度的二叉樹；

構造Huffman樹的過程：

(1)將各個節點按照權重從小到大排序；

(2)去最小權重的兩個節點，並新建一個父節點作為這兩個節點的雙親，雙親節點的權重為子節點權重之和，再將此父節點放入原來的佇列；

(3)重複(2)的步驟，直到佇列中只有一個節點，此節點為根節點；

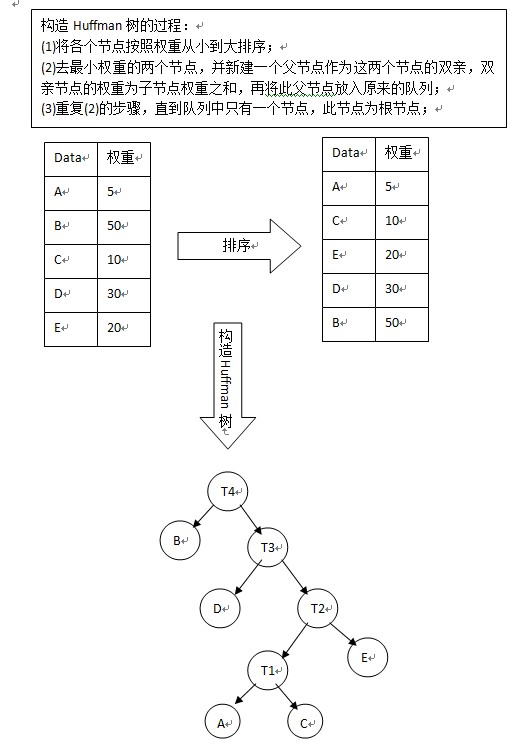
構造完Huffman樹之後，就可以進行Huffman編碼了，編碼規則：

(1)左分支填0，右分支填1；

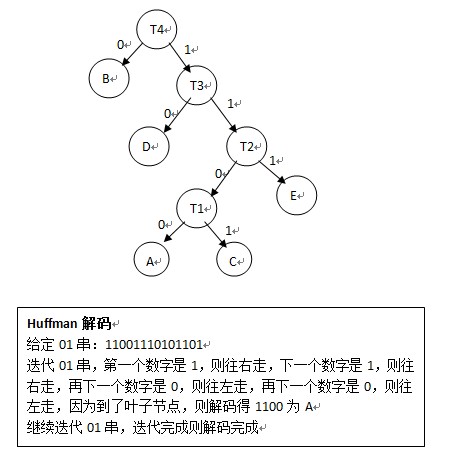
Huffman解碼過程

(1)給定一個01串，將01串進行Huffman樹，到葉子節點了就表明已經解碼一個節點，然後再次遍歷Huffman樹；