2. 程式人生 > >David Silver強化學習公開課（四）：不基於模型的預測

David Silver強化學習公開課（四）：不基於模型的預測

阿新 • • 發佈：2018-12-21

簡介 Introduction

通過先前的講解，我們明白瞭如何從理論上解決一個已知的MDP：通過動態規劃來評估一個給定的策略，並且得到最優價值函式，根據最優價值函式來確定最優策略；也可以直接進行不基於任何策略的狀態價值迭代得到最優價值函式和最優策略。

從本講開始將花連續兩講的時間討論解決一個可以被認為是MDP、但卻不掌握MDP具體細節的問題，也就是講述如何直接從Agent與環境的互動來得到一個估計的最優價值函式和最優策略。這部分內容同樣分為兩部分，第一部分也就是本講的內容，聚焦於策略評估，也就是預測，直白的說就是在給定的策略同時不清楚MDP細節的情況下，估計Agent會得到怎樣的最終獎勵。下一講將利用本講的主要觀念來進行控制進而找出最優策略，最大化Agent的獎勵。

本講內容同樣分為三個小部分，分別是蒙特卡洛強化學習、時序差分強化學習和介於兩者之間的λ時序差分強化學習。相信讀者在閱讀本講內容後會對這三類學習演算法有一定的理解。

蒙特卡洛強化學習 Monte-Carlo Reinforcement Learning

蒙特卡洛強化學習指：在不清楚MDP狀態轉移及即時獎勵的情況下，直接從經歷完整的Episode來學習狀態價值，通常情況下某狀態的價值等於在多個Episode中以該狀態算得到的所有收穫的平均。

注：收穫不是針對Episode的，它存在於Episode內，針對於Episode中某一個狀態。從這個狀態開始經歷完Episode時得到的有衰減的即時獎勵的總和。從一個Episode中，我們可以得到該Episode內所有狀態的收穫。當一個狀態在Episode內出現多次，該狀態的收穫有不同的計算方法，下文會講到。

注：與Episode比較貼近的中文是“經歷片段”，有被翻譯成“回合”，這其實並不準確反映其意思，由於一直沒找到比較準確的中文詞彙和Episode對應，因此一直在使用英文。同時也儘可能的新增一些說明來描述Episode到底是什麼。

完整的Episode 指必須從某一個狀態開始，Agent與Environment互動直到終止狀態，環境給出終止狀態的即時收穫為止。

完整的Episode不要求起始狀態一定是某一個特定的狀態，但是要求個體最終進入環境認可的某一個終止狀態。

蒙特卡洛強化學習有如下特點：不基於模型本身，直接從經歷過的Episode中學習，必須是完整的Episode，使用的思想就是用平均收穫值代替價值。理論上Episode越多，結果越準確。

  • 蒙特卡洛策略評估 Monte-Carlo Policy Evaluation

目標：在給定策略下，從一系列的完整Episode經歷中學習得到該策略下的狀態價值函式。

在解決問題過程中主要使用的資訊是一系列完整Episode。其包含的資訊有：狀態的轉移、使用的行為序列、中間狀態獲得的即時獎勵以及到達終止狀態時獲得的即時獎勵。其特點是使用有限的、完整Episode產生的這些經驗性資訊經驗性地推匯出每個狀態的平均收穫，以此來替代收穫的期望，而後者就是狀態價值。通常需要掌握完整的MDP資訊才能準確計算得到。

數學描述如下：

基於特定策略 \pi 的一個Episode資訊可以表示為如下的一個序列：

S_{1}, A_{1}, R_{2}, S_{2}, A_{2}, ..., S_{t}, A_{t}, R_{t+1}, ..., S_{k} ~ \pi

t 時刻狀態 S_{t} 的收穫：

G_{t} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-1} R_{T}

其中 T 為終止時刻。

該策略下某一狀態 s 的價值：

v_{\pi}(s) = E_{\pi} [ G_{t} | S_{t} = s ]

注： R_{t+1} 表示的是 t 時刻個體在狀態 S_{t} 獲得的即時獎勵，下文都使用這種下標來表示即時獎勵。更準確的表述為：個體在狀態 S_{t} 執行一個行為 a 後離開該狀態獲得的即時獎勵。

很多時候，即時獎勵只出現在Episode結束狀態時，但不能否認在中間狀態也可能有即時獎勵。公式裡的 R_{t} 指的是任何狀態得到的即時獎勵，這一點尤其要注意。

在狀態轉移過程中，可能發生一個狀態經過一定的轉移後又一次或多次返回該狀態，此時在一個Episode裡如何計算這個狀態發生的次數和計算該Episode的收穫呢？可以有如下兩種方法：

  • 首次訪問蒙特卡洛策略評估

在給定一個策略，使用一系列完整Episode評估某一個狀態s時，對於每一個Episode，僅當該狀態第一次出現時列入計算:

狀態出現的次數加1： N(s) \leftarrow N(s) + 1

總的收穫值更新： S(s) \leftarrow S(s) + G_{t}

狀態s的價值： V(s) = S(s) / N(s)

當 N(s) \rightarrow \infty 時， V(s) \rightarrow v_{\pi}(s)

  • 每次訪問蒙特卡洛策略評估

在給定一個策略，使用一系列完整Episode評估某一個狀態s時，對於每一個Episode，狀態s每次出現在狀態轉移鏈時，計算的具體公式與上面的一樣，但具體意義不一樣。

狀態出現的次數加1： N(s) \leftarrow N(s) + 1

總的收穫值更新： S(s) \leftarrow S(s) + G_{t}

狀態s的價值： V(s) = S(s) / N(s)

當 N(s) \rightarrow \infty 時， V(s) \rightarrow v_{\pi}(s)

  • 示例：二十一點遊戲 Blackjack Example

該示例解釋了Model-Free下的策略評估問題和結果，沒有說具體的學習過程。

狀態空間：（多達200種，根據對狀態的定義可以有不同的狀態空間，這裡採用的定義是牌的分數，不包括牌型）

  1. 當前牌的分數（12 - 21），低於12時，你可以安全的再叫牌，所以沒意義。
  2. 莊家出示的牌（A - 10），莊家會顯示一張牌面給玩家
  3. 我有“useable” ace嗎？（是或否）A既可以當1點也可以當11點。

行為空間：

  1. 停止要牌 stick
  2. 繼續要牌 twist

獎勵（停止要牌）：

  1. +1：如果你的牌分數大於莊家分數
  2. 0： 如果兩者分數相同
  3. -1：如果你的牌分數小於莊家分數

獎勵（繼續要牌）：

  1. -1：如果牌的分數>21，並且進入終止狀態
  2. 0：其它情況

狀態轉換（Transitions）：如果牌分小於12時，自動要牌

當前策略：牌分只要小於20就繼續要牌。

求解問題：評估該策略的好壞。

求解過程：使用莊家顯示的牌面值、玩家當前牌面總分值來確定一個二維狀態空間，區分手中有無A分別處理。統計每一牌局下決定狀態的莊家和玩家牌面的狀態資料，同時計算其最終收穫。通過模擬多次牌局，計算每一個狀態下的平均值，得到如下圖示。

最終結果：無論玩家手中是否有A牌，該策略在絕大多數情況下各狀態價值都較低，只有在玩家拿到21分時狀態價值有一個明顯的提升。

                                                   

這個例子只是使讀者對蒙特卡洛策略評估方法有一個直觀的認識。

為了儘可能使讀者對MC方法有一個直接的認識，我們嘗試模擬多個二十一點遊戲牌局資訊，假設我們僅研究初始狀態下莊家一張明牌為4，玩家手中前兩張牌和為15的情形，不考慮A牌。在給定策略下，玩家勢必繼續要牌，則可能會出現如下多種情形：

                                   

注意：莊家不需遵循個體的當前策略。

可以看到，使用只有當牌不小於20的時候才停止叫牌這個策略，前6次平均價值為0，如果玩的牌局足夠多，按照這樣的方法可以針對每一個狀態（莊家第一張明牌，玩家手中前兩張牌分值合計）都可以製作這樣一張表，進而計算玩家獎勵的平均值。通過結果，可以發現這個策略並不能帶來很高的玩家獎勵。

這裡給出表中第一個對局對應的資訊序列（Episode）：

S_0<4,15>, A_0 <要牌>, R_1 <0>, S_1 <4,20>, A_1 <停止要牌>, R_2 <+1>.

可以看出，這個完整的Episode中包含兩個狀態，其中第一個狀態的即時獎勵為0，後一個狀態是終止狀態，根據規則，玩家贏得對局，獲得終止狀態的即時獎勵+1。讀者可以加深對即時獎勵、完整Episode的理解。

在使用蒙特卡洛方法求解平均收穫時，需要計算平均值。通常計算平均值要預先儲存所有的資料，最後使用總和除以此次數。這裡介紹了一種更簡單實用的方法：

  • 累進更新平均值 Incremental Mean

這裡提到了在實際操作時常用的一個實時更新均值的辦法，使得在計算平均收穫時不需要儲存所有既往收穫，而是每得到一次收穫，就計算其平均收穫。

理論公式如下：

                                                                 

這個公式比較簡單。把這個方法應用於蒙特卡洛策略評估，就得到下面的蒙特卡洛累進更新。

  • 蒙特卡洛累進更新

對於一系列Episodes中的每一個： S_{1}, A_{1}, R_{2}, S_{2}, A_{2}, ..., S_{t}, A_{t}, R_{t+1}, ..., S_{k}

對於Episode裡的每一個狀態 S_{t} ，有一個收穫 G_{t} ，每碰到一次 S_{t} ,使用下式計算狀態的平均價值 V(S_{t}) ：

                                                        

其中：

                                                                 

在處理非靜態問題時，使用這個方法跟蹤一個實時更新的平均值是非常有用的，可以扔掉那些已經計算過的Episode資訊。此時可以引入引數 \alpha 來更新狀態價值：

                                                          

以上就是蒙特卡洛學習方法的主要思想和描述，由於蒙特卡洛學習方法有許多缺點（後文會細說），因此實際應用並不多。接下來介紹實際常用的TD學習方法。

時序差分學習 Temporal-Difference Learning

時序差分學習簡稱TD學習，它的特點如下：和蒙特卡洛學習一樣，它也從Episode學習，不需要了解模型本身；但是它可以學習不完整的Episode，通過自身的引導（bootstrapping），猜測Episode的結果，同時持續更新這個猜測。

我們已經學過，在Monte-Carlo學習中，使用實際的收穫（return） G_{t} 來更新價值（Value）：

V(S_{t}) \leftarrow V(S_{t}) + \alpha (G_{t} - V(S_{t}))

在TD學習中，演算法在估計某一個狀態的價值時，用的是離開該狀態的即刻獎勵 R_{t+1} 與下一狀態 S_{t+1} 的預估狀態價值乘以衰減係數(\gamma)組成，這符合Bellman方程的描述：

V(S_{t}) \leftarrow V(S_{t}) + \alpha (R_{t+1} + \gamma V(S_{t+1}) - V(S_{t}))

式中：

R_{t+1} + \gamma V(S_{t+1}) 稱為 TD目標值

\delta_{t} = R_{t+1} + \gamma V(S_{t+1}) - V(S_{t}) 稱為TD誤差

BootStrapping 指的就是TD目標值 R_{t+1} + \gamma V(S_{t+1}) 代替收穫 G_t 的過程，暫時把它翻譯成“引導”。

下面用一個例子直觀解釋蒙特卡洛策略評估和TD策略評估的差別。

  • 示例——駕車返家

想象一下你下班後開車回家，需要預估整個行程花費的時間。假如一個人在駕車回家的路上突然碰到險情：對面迎來一輛車感覺要和你相撞，嚴重的話他可能面臨死亡威脅，但是最後雙方都採取了措施沒有實際發生碰撞。如果使用蒙特卡洛學習，路上發生的這一險情可能引發的負向獎勵不會被考慮進去，不會影響總的預測耗時；但是在TD學習時，碰到這樣的險情，這個人會立即更新這個狀態的價值，隨後會發現這比之前的狀態要糟糕，會立即考慮決策降低速度贏得時間，也就是說你不必像蒙特卡洛學習那樣直到他死亡後才更新狀態價值，那種情況下也無法更新狀態價值。

TD演算法相當於在整個返家的過程中（一個Episode），根據已經消耗的時間和預期還需要的時間來不斷更新最終回家需要消耗的時間。

                                               

基於上表所示的資料，下圖展示了蒙特卡洛學習和TD學習兩種不同的學習策略來更新價值函式（各個狀態的價值）。這裡使用的是從某個狀態預估的到家還需耗時來間接反映某狀態的價值：某位置預估的到家時間越長，該位置價值越低，在優化決策時需要避免進入該狀態。對於蒙特卡洛學習過程，駕駛員在路面上碰到各種情況時，他不會更新對於回家的預估時間，等他回到家得到了真實回家耗時後，他會重新估計在返家的路上著每一個主要節點狀態到家的時間，在下一次返家的時候用新估計的時間來幫助決策；而對於TD學習，在一開始離開辦公室的時候你可能會預估總耗時30分鐘，但是當你取到車發現下雨的時候，你會立刻想到原來的預計過於樂觀，因為既往的經驗告訴你下雨會延長你的返家總時間，此時你會更新目前的狀態價值估計，從原來的30分鐘提高到40分鐘。同樣當你駕車離開高速公路時，會一路根據當前的狀態（位置、路況等）對應的預估返家剩餘時間，直到返回家門得到實際的返家總耗時。這一過程中，你會根據狀態的變化實時更新該狀態的價值。

                                    

通過這個例子，我們可以直觀的瞭解到：

MC對比 TD之一

TD 在知道結果之前可以學習，MC必須等到最後結果才能學習；

TD 可以在沒有結果時學習，可以在持續進行的環境裡學習。

MC對比 TD之二

G_{t} ：實際收穫，是基於某一策略狀態價值的無偏估計

                                             

TD target：TD目標值，是基於下一狀態預估價值計算的當前預估收穫，是當前狀態實際價值的有偏估計

                                                              

True TD target： 真實TD目標值，是基於下一狀態的實際價值對當前狀態實際價值的無偏估計

                                                                 

MC 沒有偏倚（bias），但有著較高的變異性（Variance），且對初始值不敏感；

TD 低變異性variance, 但有一定程度的bias，對初始值較敏感，通常比 MC 更高效；

這裡的偏倚指的是距離期望的距離，預估的平均值與實際平均值的偏離程度；變異性指的是方差，評估單次取樣結果相對於與平均值變動的範圍大小。基本就是統計學上均值與方差的概念。

對於MC和TD的區別，還可以用下面的例子來加深理解：

  • 示例——隨機行走

狀態空間：如下圖：A、B、C、D、E為中間狀態，C同時作為起始狀態。灰色方格表示終止狀態；

                                      

行為空間：除終止狀態外，任一狀態可以選擇向左、向右兩個行為之一；

即時獎勵：右側的終止狀態得到即時獎勵為1，左側終止狀態得到的即時獎勵為0，在其他狀態間轉化得到的即時獎勵是0；

狀態轉移：100%按行為進行狀態轉移，進入終止狀態即終止；

衰減係數：1；

給定的策略：隨機選擇向左、向右兩個行為。

問題：對這個MDP問題進行預測，也就是評估隨機行走這個策略的價值，也就是計算該策略下每個狀態的價值，也就是確定該MDP問題的狀態價值函式。

求解：下圖是使用TD演算法得到的結果。橫座標顯示的是狀態，縱座標是各狀態的價值估計，一共5條折線，數字表明的是實際經歷的Episode數量，true value所指的那根折線反映的是各狀態的實際價值。第0次時，各狀態的價值被初始化為0.5，經過1次、10次、100次後得到的價值函式越來越接近實際狀態價值函式。

                                           

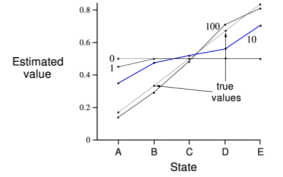
下圖比較了MC和TD演算法的效率。橫座標是經歷的Episode數量，縱座標是計算得到的狀態函式和實際狀態函式下各狀態價值的均方差。黑色是MC演算法在不同step-size下的學習曲線，灰色的曲線使用TD演算法。可以看出TD較MC更高效。此圖還可以看出當step-size不是非常小的情況下，TD有可能得不到最終的實際價值，將會在某一區間震盪。

                                              

  • 示例——AB

已知：現有兩個狀態(A和B)，MDP未知，衰減係數為1，有如下表所示8個完整Episode的經驗及對應的即時獎勵，其中除了第1個Episode有狀態轉移外，其餘7個均只有一個狀態。

                                                    

問題：依據僅有的Episode，計算狀態A，B的價值分別是多少，即V(A)=？， V(B)=？

答案：V(B) = 6/8，V(A)根據不同演算法結果不同，用MC演算法結果為0，TD則得出6/8。

解釋：應用MC演算法，由於需要完整的Episode,因此僅Episode1可以用來計算A的狀態價值，很明顯是0；同時B的價值是6/8。應用TD演算法時，TD演算法試圖利用現有的Episode經驗構建一個MDP（如下圖），由於存在一個Episode使得狀態A有後繼狀態B，因此狀態A的價值是通過狀態B的價值來計算的，同時經驗表明A到B的轉移概率是100%，且A狀態的即時獎勵是0，並且沒有衰減，因此A的狀態價值等於B的狀態價值。

                                                         

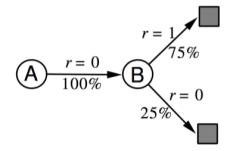
MC演算法試圖收斂至一個能夠最小化狀態價值與實際收穫的均方差的解決方案，這一均方差用公式表示為：

                                                                

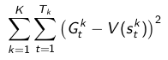
式中， k 表示的是Episode序號， K 為總的Episode數量， t 為一個Episode內狀態序號（第1,2,3...個狀態等）， T_{k} 表示的是第 k 個Episode總的狀態數， G^{k}_{t} 表示第 k 個Episode裡 t時刻狀態 S_{t} 獲得的最終收穫， V(S^{k}_{t}) 表示的是第 k 個Episode裡演算法估計的 t 時刻狀態 S_{t} 的價值。

TD演算法則收斂至一個根據已有經驗構建的最大可能的馬兒可夫模型的狀態價值，也就是說TD演算法將首先根據已有經驗估計狀態間的轉移概率：

                                                   

同時估計某一個狀態的即時獎勵：

                                                     

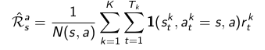
最後計算該MDP的狀態函式。

MC對比 TD之三

通過比較可以看出，TD演算法使用了MDP問題的馬兒可夫屬性，在Markov 環境下更有效；但是MC演算法並不利用馬兒可夫屬性，通常在非Markov環境下更有效。

  • 小結——三種強化學習演算法

Monte-Carlo, Temporal-Difference 和 Dynamic Programming 都是計算狀態價值的一種方法，區別在於，前兩種是在不知道Model的情況下的常用方法，這其中又以MC方法需要一個完整的Episode來更新狀態價值，TD則不需要完整的Episode；DP方法則是基於Model（知道模型的運作方式）的計算狀態價值的方法，它通過計算一個狀態S所有可能的轉移狀態S’及其轉移概率以及對應的即時獎勵來計算這個狀態S的價值。

關於是否Bootstrap：MC 沒有引導資料，只使用實際收穫；DP和TD都有引導資料。

關於是否用樣本來計算: MC和TD都是應用樣本來估計實際的價值函式；而DP則是利用模型直接計算得到實際價值函式，沒有樣本或採樣之說。

下面的幾張圖直觀地體現了三種演算法的區別：

                                                   

MC: 取樣，一次完整經歷，用實際收穫更新狀態預估價值

                                                    

TD：取樣，經歷可不完整，用喜愛狀態的預估狀態價值預估收穫再更新預估價值

                                                   

DP：沒有采樣，根據完整模型，依靠預估資料更新狀態價值

                                                  

上圖從兩個維度解釋了四種演算法的差別，多了一個窮舉法。這兩個維度分別是：取樣深度和廣度。當使用單個取樣，同時不走完整個Episode就是TD；當使用單個取樣但走完整個Episode就是MC；當考慮全部樣本可能性，但對每一個樣本並不走完整個Episode時，就是DP；當既考慮所有Episode又把Episode從開始到終止遍歷完，就變成了窮舉法。

需要提及的是：DP利用的是整個MDP問題的模型，也就是狀態轉移概率，雖然它並不實際利用樣本，但是它利用了整個模型的規律，因此認為是Full Width的。

TD(λ)

先前所介紹的TD演算法實際上都是TD(0)演算法，括號內的數字0表示的是在當前狀態下往前多看1步，要是往前多看2步更新狀態價值會怎樣？這就引入了n-step的概念。

  • n-步預測 n-Step Prediction

在當前狀態往前行動n步，計算n步的return，同樣TD target 也由2部分組成，已走的步數使用確定的即時reward，剩下的使用估計的狀態價值替代。

                                              

注：圖中空心大圓圈表示狀態，實心小圓圈表示行為

  • n-步收穫

TD或TD(0)是基於1-步預測的，MC則是基於∞-步預測的：

                        

注意：n=2時不寫成TD(2)。

定義n-步收穫：

                                

那麼，n步TD學習狀態價值函式的更新公式為：

                                        

既然存在n-步預測，那麼n=？時效果最好呢，下面的例子試圖回答這個問題：

  • 示例——大規模隨機行走

這個示例研究了使用多個不同步數預測聯合不同步長(step-size，公式裡的係數α）時，分別在線上和離線狀態時狀態函式均方差的差別。所有研究使用了10個Episode。離線與線上的區別在於，離線是在經歷所有10個Episode後進行狀態價值更新；而線上則至多經歷一個Episode就更新依次狀態價值。

                                                

結果如圖表明，離線和線上之間曲線的形態差別不明顯；從步數上來看，步數越長，越接近MC演算法，均方差越大。對於這個大規模隨機行走示例，線上計算比較好的步數是3-5步，離線計算比較好的是6-8步。但是不同的問題其對應的比較高效的步數不是一成不變的。因此選擇多少步數作為一個較優的計算引數也是一個問題。

這裡我們引入了一個新的引數：λ。通過引入這個新的引數，可以做到在不增加計算複雜度的情況下綜合考慮所有步數的預測。這就是λ預測和λ收穫。

  • λ-收穫

λ-收穫 G_{t}^{\lambda} 綜合考慮了從 1 到 \infty 的所有步收穫，它給其中的任意一個 n- 步收穫施加一定的權重 (1-\lambda)\lambda^{n-1} 。通過這樣的權重設計，得到如下的公式：

                                                              

對應的λ-預測寫成TD(λ):

                                                            

下圖是各步收穫的權重分配圖，圖中最後一列λ的指數是 T-t-1 。 T 為終止狀態的時刻步數， t 為當前狀態的時刻步數，所有的權重加起來為1。

                                                    

  • TD(λ)對於權重分配的圖解

                           

這張圖還是比較好理解，例如對於n=3的3-步收穫，賦予其在 \lambda 收穫中的權重如左側陰影部分面積，對於終止狀態的T-步收穫，T以後的所有陰影部分面積。而所有節段面積之和為1。這種幾何級數的設計也考慮了演算法實現的計算方便性。

TD((λ)的設計使得Episode中，後一個狀態的狀態價值與之前所有狀態的狀態價值有關，同時也可以說成是一個狀態價值參與決定了後續所有狀態的狀態價值。但是每個狀態的價值對於後續狀態價值的影響權重是不同的。我們可以從兩個方向來理解TD(λ)：

前向認識TD(λ)

引入了λ之後，會發現要更新一個狀態的狀態價值，必須要走完整個Episode獲得每一個狀態的即時獎勵以及最終狀態獲得的即時獎勵。這和MC演算法的要求一樣，因此TD(λ)演算法有著和MC方法一樣的劣勢。λ取值區間為[0,1]，當λ=1時對應的就是MC演算法。這個實際計算帶來了不便。

反向認識TD(λ)

TD(λ)從另一方面提供了一個單步更新的機制，通過下面的示例來說明。

  • 示例——被電擊的原因

這是之前見過的一個例子，老鼠在連續接受了3次響鈴和1次亮燈訊號後遭到了電擊，那麼在分析遭電擊的原因時，到底是響鈴的因素較重要還是亮燈的因素更重要呢？

                                                              

兩個概念：

頻率啟發 Frequency heuristic：將原因歸因於出現頻率最高的狀態

就近啟發 Recency heuristic：將原因歸因於較近的幾次狀態

給每一個狀態引入一個數值：效用追蹤（Eligibility Traces, ES，也有翻譯成“資質追蹤”，這是同一個概念從兩個不同的角度理解得到的不同翻譯），可以結合上述兩個啟發。定義：

E_{0}(s) = 0

E_{t}(s) = \gamma \lambda E_{t-1}(s) + 1(S_{t} = s)

其中 1(S_{t} = s) 是一個條件判斷表示式。

下圖給出了 E_{t}(s) 對於 t 的一個可能的曲線圖：

                                          

該圖橫座標是時間，橫座標下有豎線的位置代表當前進入了狀態 s ，縱座標是效用追蹤值 E 。可以看出當某一狀態連續出現，E值會在一定衰減的基礎上有一個單位數值的提高，此時將增加該狀態對於最終收穫貢獻的比重，因而在更新該狀態價值的時候可以較多地考慮最終收穫的影響。同時如果該狀態距離最終狀態較遠，則其對最終收穫的貢獻越小，在更新該狀態時也不需要太多的考慮最終收穫。

特別的， E 值並不需要等到完整的Episode結束才能計算出來，它可以每經過一個時刻就得到更新。 E 值存在飽和現象，有一個瞬時最高上限： E_{max} = 1/(1-\gamma\lambda)

把剛才的描述體現在公式裡更新狀態價值，是這樣的：

                                                              

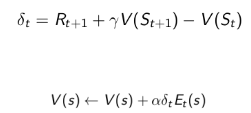
注：每一個狀態都有一個 E 值， E 值隨時間而變化。

當λ=0時，只有當前狀態得到更新，等同於TD(0)演算法；

當λ=1時，TD(1)粗略看與每次訪問的MC演算法等同；線上更新時，狀態價值差每一步都會有積累；離線更新時，TD(1)等同於MC演算法。

注：ET是一個非常符合神經科學相關理論的、非常精巧的設計。把它看成是神經元的一個引數，它反映了神經元對某一刺激的敏感性和適應性。神經元在接受刺激時會有反饋，在持續刺激時反饋一般也比較強，當間歇一段時間不刺激時，神經元又逐漸趨於靜息狀態；同時不論如何增加刺激的頻率，神經元有一個最大飽和反饋。

小結

 下表給出了λ取各種值時，不同演算法在不同情況下的關係。                                         

                                   

相較於MC演算法，TD演算法應用更廣，是一個非常有用的強化學習方法，在下一講講解控制相關的演算法時會詳細介紹TD演算法的實現。

相關推薦

David Silver強化學習公開課（四）：不基於模型的預測

簡介 Introduction 通過先前的講解，我們明白瞭如何從理論上解決一個已知的MDP：通過動態規劃來評估一個給定的策略，並且得到最優價值函式，根據最優價值函式來確定最優策略；也可以直接進行不基於任何策略的狀態價值迭代得到最優價值函式和最優策略。 從本講開始將花連續兩

David Silver強化學習公開課（一）：馬爾科夫決策過程

在強化學習中，馬爾科夫決策過程（Markov decision process, MDP）是對完全可觀測的環境進行描述的，也就是說觀測到的狀態內容完整地決定了決策的需要的特徵。幾乎所有的強化學習問題都可以轉化為MDP。本講是理解強化學習問題的理論基礎。 馬爾科夫過程 M

David Silver強化學習課程筆記（五）

第五課：模型無關的控制         本文主要介紹模型無關的控制，包括同策略方法（On-Policy，也譯作“在策略”）和異策略（Off-Policy，也譯作“離策略”）方法，由於是模型無關，因此本文聊的是學習（learning），而不是規劃（planning）。   

David Silver強化學習課程筆記（三）

第三課：動態規劃        課程標題本來是“Planning by Dynamic Programming”，應該翻譯為”利用動態規劃方法進行規劃“，但是感覺有點長，所以就使用”動態規劃“作為標題，大家理解就好......        先說下這節課講的主要內容，主要有：

David Silver強化學習課程筆記（一）

        大家好，我是微念。         國慶這些天大致學習了一下David Silver的強化學習課程，感覺挺受用的，大家可以去百度雲盤（無字幕版本）下載視訊，或者去B站搜尋觀看（有字幕版本），課程課件下載地址為David Silver課程課件。       

David Silver強化學習課程筆記（八）（下）

第八課（下）：基於Simulation的搜尋方法         在《第八課（上）：學習與規劃的結合》中，我們講到了Model-Based RL方法，在該方法中，我們首先擬合得到一個模型，然後可以利用各種規劃方法進行規劃，或者，可以引申出Sample-Based Plann

我的機器學習之旅（四）：回歸與工程應用

多個 算法 ati function RR numpy pen 圖片 bsp 內容:線性回歸；邏輯回歸，應用場景。 一、線性回歸 有監督學習，根據學習樣本{x->y},學習一個映射f：X->Y(線性相關),輸出預測結果y_i。最簡單的例子：y=ax+b 重要組成

深度學習之 TensorFlow（四）：卷積神經網絡

padding valid 叠代 val 分析 此外 nbsp drop BE 基礎概念： 　　卷積神經網絡（CNN）：屬於人工神經網絡的一種，它的權值共享的網絡結構顯著降低了模型的復雜度，減少了權值的數量。卷積神經網絡不像傳統的識別算法一樣，需要對數據進行特征提取和數據重

【活動報名】NEO 區塊鏈公開課（1）： NEO 區塊鏈開發入門

NEO 區塊鏈公開課是 NGD （ NEO Global Development )、NEL （ NewEconoLab ）、InnoSpace 創新院共同發起的區塊鏈技術學習專場活動。旨在滿足廣大開發者對 NEO 區塊鏈技術的入門、進階以及技能提升需求。 精心設計的課程內容，資深技術講師

【活動預告】NEO區塊鏈公開課（5）：NNS系統設計與實現

NEO區塊鏈公開課第5期： 主題：NEL精品課程之NNS系統設計與實現 時間：10月20日13：30—17：00   地點：上海市楊浦區政學路77號INNOSPACE 1樓IPOCLUB   報名連結：http://www.huodongxing.c

Linux 學習之路（四）：管道、重定向、正則

管道及IO重定向 運算器、控制器：CPU 儲存器：RAM 輸入裝置/輸出裝置 程式：指令和資料 控制器：指令 運算器： 儲存器： 地址匯流排：記憶體定址 資料匯流排：傳輸資料 控制匯流排：控制指令 暫存器：CPU暫時儲存器 I/O:硬碟 系

機器學習實戰教程（四）：樸素貝葉斯基礎篇之言論過濾器

word 最可 dog 一個 mac github上 開課 和數 基礎上 原文鏈接： Jack-Cui，https://cuijiahua.com/blog/2017/11/ml_4_bayes_1.html 一、前言 樸素貝葉斯算法是有監督的學習算法，解決的是分類問題，

EventBus原始碼分析（四）：執行緒模型分析（2.4版本）

EventBus有四種執行緒模型 PostThread模式不需執行緒切換，直接在釋出者執行緒進行事件處理。 MainThread模式分類討論：釋出者執行緒是主執行緒則直接呼叫事件處理方法，否則通過Handler進行執行緒切換，切換到主執行緒處理事件，該模

GAN學習之路（二）：遷移式模型

遷移變換 以CycleGAN為例，遷移就是從一個域遷移到另一個域。比如：斑馬到馬； 與CycleGAN很有關係的兩個兄弟DualGAN和DiscoGAN； CycleGAN的歷史淵源 階段一：cGAN，條件是標註資訊； 階段二：pix2pix，條件是圖片資訊；

Picasso原始碼分析（四）：不變模式、建造者模式和Request的預處理

Request的不變模式（Immutable Pattern） 　　不變模式可增強物件的強壯型，允許多個物件共享某一個物件，降低了對該物件進行併發訪問時的同步化開銷。如果需要修改一個不變物件的狀態，那麼就需要建立一個新的同類型物件，並在建立時將這個新的狀態

機器學習回顧篇（10）：感知機模型

  注：本系列所有部落格將持續更新併發布在github和gitee上，您可以通過github、gitee下載本系列所有文章筆記檔案。   1 引言¶ 感知機是一種簡單且易於實現的二分類判別模型，主要思想是通過誤分類

David Silver 強化學習Lecture3：Dynamic Programming

    David Silver 強化學習系列部落格的內容整理自David Silver 強化學習的PPT和知乎葉強強化學習專欄。 1 Introduction 1.1 What is Dynamic Programming?     Dynami

David Silver 強化學習Lecture4：Model-Free Prediction

    David Silver強化學習系列部落格的內容整理自David Silver 強化學習的PPT和知乎葉強強化學習專欄。 1 Introduction     前三節筆記中，通過動態規劃能夠解決環境已知的MDP問題，也就是已知<S,A,P,

David Silver強化學習Lecture1：強化學習簡介

優化 計算 rod 簡介 因此 roc 課件 布局 表示 課件：Lecture 1: Introduction to Reinforcement Learning 視頻：David Silver深度強化學習第1課 - 簡介 (中文字幕) 強化學習的特征 作為機器學習的

python學習之路（四）

[1] size class dex epc uri msu 語句 這就是 繼續昨天的學習，學到了數組。 首先有兩個數組，name1和name2.我們可以將兩個數組合並 name1=[1,2,3,4] name2=[5,6,7,8] names=name1.extend(