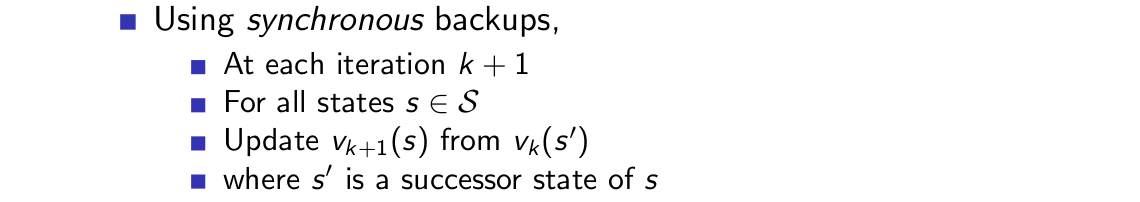David Silver強化學習課程筆記(三)
第三課:動態規劃
課程標題本來是“Planning by Dynamic Programming”,應該翻譯為”利用動態規劃方法進行規劃“,但是感覺有點長,所以就使用”動態規劃“作為標題,大家理解就好......
先說下這節課講的主要內容,主要有:策略估計、策略迭代、值迭代、動態規劃擴充套件、收縮對映定理。其中策略估計主要介紹如何利用迭代方法對策略的值函式進行估計,也即我們在第一課中討論的問題;策略迭代與值迭代則是在策略估計的基礎上,引入策略改進,從而達到控制的目的,二者的主要區別是策略迭代基於貝爾曼期望方程和貪婪法,而值迭代則是基於貝爾曼最優方程;動態規劃擴充套件介紹了幾種改進方法;最後的收縮對映證明了策略迭代與值迭代都將收斂到最優策略。
1.動態規劃簡介
什麼是動態規劃(DP)?課程中給出了這樣的釋義:Dynamic means the sequential or temporal component to the problem; Programming means optimising a "program", i.e. a policy。就是說”動態“指的是該問題的時間序貫部分,”規劃“指的是去優化一個計劃,換句話說,優化一個策略。
動態規劃通常分為三步:a)將問題分解為子問題;b)求解子問題;c)合併子問題的解。
是不是所有問題都能用動態規劃求解呢?不是的,動態規劃方法需要我們的問題包含以下兩個性質:
a)最優子結構:保證問題能夠使用最優性準則,從而問題的最優解可以分解為子問題最優解;
b)重疊子問題:子問題重複出現多次,因而我們可以快取並重用子問題的解。
恰巧,MDP滿足上面兩個性質,貝爾曼方程給出了問題的迭代分解,值函式儲存和重用問題的解。因此,我們可以利用動態規劃方法來求解MDP規劃問題,此時假定MDP的模型是已知的,DP方法既可用於預測,也可用於控制:
2.迭代策略估計
策略估計指的是對於某一個給定的策略,估計其值函式。一般來說,我們通過迭代使用貝爾曼期望方程backup來進行求解(這裡說到的backup也即
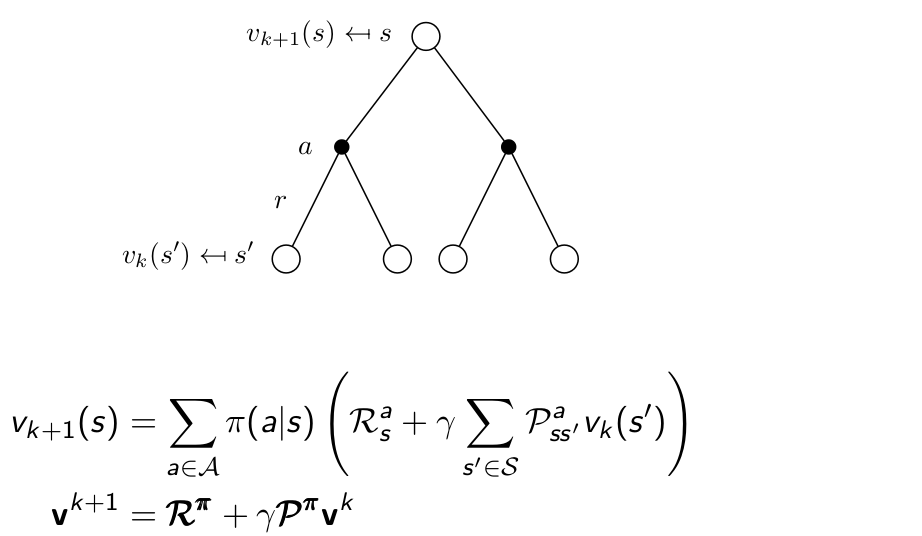
首先我們討論同步backup,在後面”幾種動態規劃的改進方法“中討論如何使用非同步backup。同步backup步驟如下:
其示意圖如下:
也即,我們利用上一個時間步的值函式來更新當前時間步的值函式,迭代應用這一更新公式,從而收斂至策略對應的真實值函式。
3.策略迭代
上一個小節中我們討論瞭如何使用貝爾曼期望方程進行策略估計,並沒有對策略進行改進,也就是說,策略還是那個策略,而如果我們要解決控制問題,而不是預測問題的話,對策略進行改進是必要的,我們總是希望去找到某個問題的最優策略。如何改進策略?可以通過對於old policy的值函式採用貪婪法即可得到改進的策略:
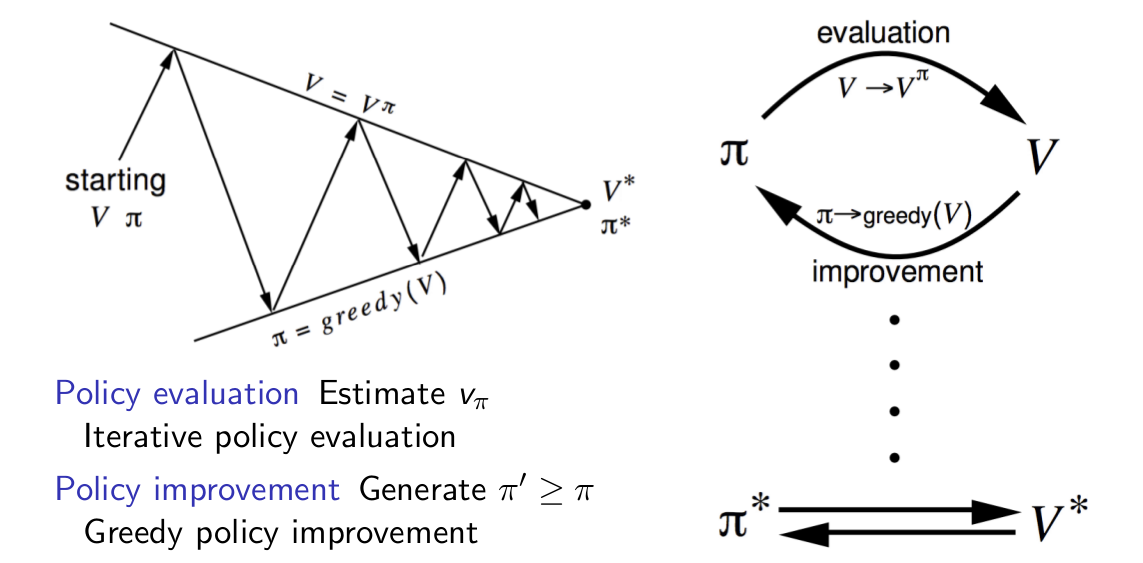
對於較小的格子世界問題,上面這兩步操作可以直接得到最優策略,但是通常來說,我們需要更多的估計/改進迭代(也即我們給出一個初始策略,估計其值函式至接近真實值,然後利用貪婪方法得到改進的策略,接著對改進後的策略進行估計......)。儘管如此,我們的策略迭代方法總能收斂到最優策略,下面用示意圖來表示策略迭代的過程:
我們可以對貪婪法總能對策略做出改進這一現象進行證明:
如果整個策略迭代完成,則上述證明中的等號成立,此時貝爾曼最優方程得以滿足,也即最終得到的策略是最優策略,其值函式是最優值函式。
策略迭代在每一個迭代步總是先對策略進行值函式估計,直至收斂,那我們能否在策略估計還未收斂時就進行策略改進呢?比如說引入epsilon收斂 ,比如簡單地在對策略估計迭代k次之後就進行策略改進,甚至,k=1就進行策略改進又會怎麼樣呢?下面我們將會講到,k=1的情形就是值迭代方法。
此外,我們可以將策略迭代方法拓展到一般化的策略迭代方法:首先估計策略的值函式,然後使用任意策略改進演算法對策略進行改進,例如這裡的greedy方法,迭代執行這兩步,直至收斂即可。
4.值迭代
說到值迭代,先聊一聊最優性原理總是好的,畢竟本文開頭就聊到了策略迭代是基於貝爾曼期望方程和貪婪法的,而值迭代則是基於貝爾曼最優方程的,所以我們先看一下最優性原理:
通俗地說,最優性原理可以理解為:對於某一個最優決策序列而言,不論初始狀態和初始決策如何,對於前面決策所造成的某一狀態而言,其後各階段的決策序列必須構成最優策略。對於值函式使用最優性原理:
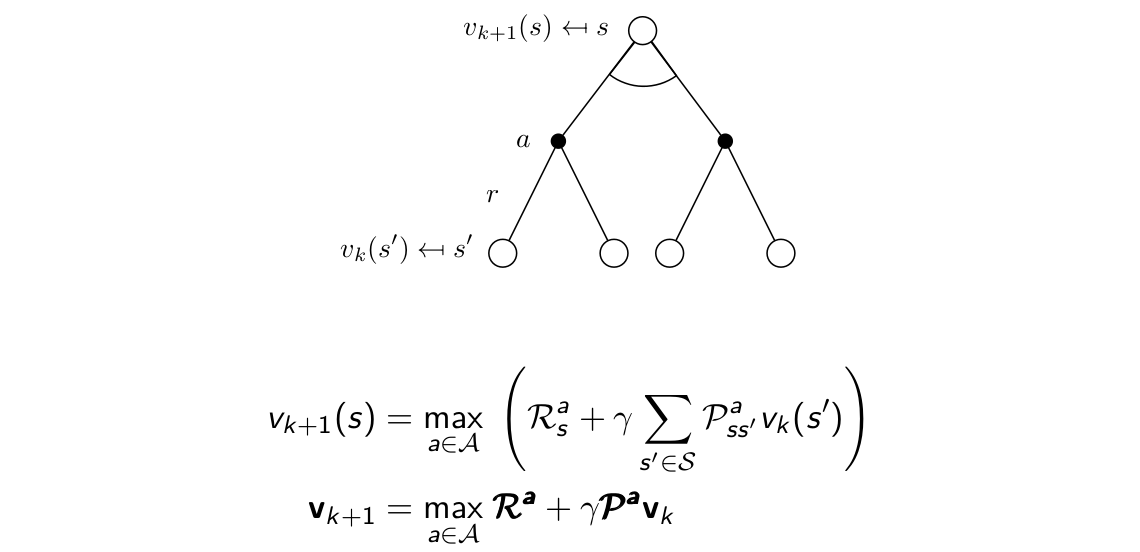
我們可以看一下值迭代的步驟:
與策略迭代一樣,值迭代最終也同樣收斂到最優值函式,不過,與策略迭代不一樣的是,值迭代沒有顯式的策略,它通過貝爾曼最優方程,隱式地實現了策略改進這一步。值得注意的是,中間過程中的值函式可能並不對應於任何策略。我們通過backup圖來對值迭代進行理解:
與貝爾曼期望方程相比,貝爾曼最優方程將期望操作變為最大操作,也即隱式地實現了策略改進這一步,不過是固定為greedy的,而不是其他策略改進方法,我們通過greedy得到的策略通常為確定性策略。
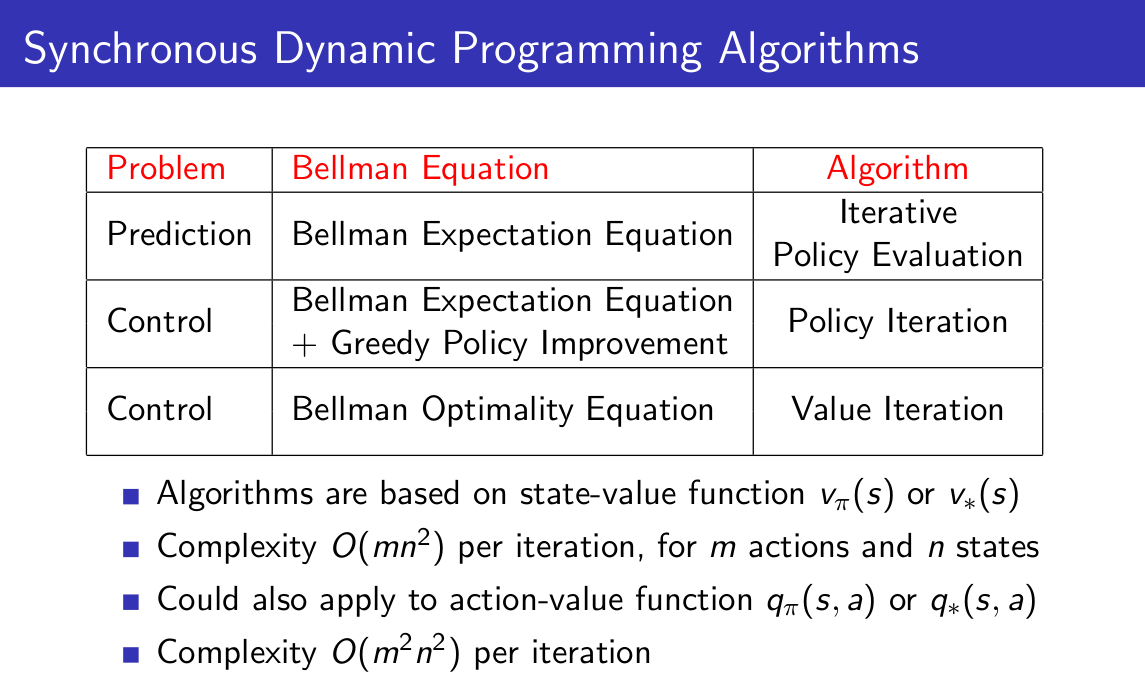
5.策略估計、策略迭代、值迭代總結
關於複雜度的計算說明一下,比如對於貝爾曼最優方程更新狀態值函式,首先對於某一個狀態s對應的值,我們需要將轉移之後的狀態s'乘以轉移矩陣求和,計算複雜度為n,其次對於m個動作求最大,複雜度為m,最後,所有n個狀態都要更新,因此總的計算複雜度為m*n^2;而對於動作值函式的更新,為(s',a')->(s,a),也即m*n->m*n,所以總計算複雜度為(m^2)*(n^2)。
6.動態規劃擴充套件
首先介紹非同步動態規劃,前面我們介紹的方法都是用的同步動態規劃,也就是說,所有的狀態一起進行backup,而非同步動態規劃則是將所有states獨立進行backup,並且是以任意順序。非同步動態規劃可以減少計算量,不過如果想要收斂,則需要滿足一個條件:所有狀態都需要能夠持續被選擇,或者說,在任一時刻,任何狀態都有可能被選中。非同步動態規劃主要有三個簡單的idea:
1)In-place dynamic programming;
2)Prioritised sweeping;
3)Real-time dynamic programming.
直接放圖啦:
對於DP而言,它的推演是整個樹狀散開的,我們稱這種方法為Full-Width Backup方法。在這種方法中,對於每一次backup來說,所有的後繼狀態和動作都要被考慮在內,並且需要已知MDP的轉移矩陣與獎勵函式,因此DP將面臨維數災難問題。所以我們就有了Sample Backup,這種方法將在後面進行介紹,其主要思想是利用樣本進行backup,優點有a)Model-free;b)避免了維數災難問題;c)backup的代價與狀態數n無關。如下圖所示:
最後介紹一種DP的擴充套件,叫做近似動態規劃:
7.收縮對映定理
關於收縮對映定理的具體介紹見泛函分析的教材,這裡就不贅述了,定理如下:
該定理可以用於證明策略迭代、值迭代的收斂性,具體證明就不在這列出來咯~
最後關於動態規劃的擴充套件以及收縮對映定理證明迭代性說得比較籠統,有什麼問題可以留言哈~
相關推薦
David Silver強化學習課程筆記(三)
第三課:動態規劃 課程標題本來是“Planning by Dynamic Programming”,應該翻譯為”利用動態規劃方法進行規劃“,但是感覺有點長,所以就使用”動態規劃“作為標題,大家理解就好...... 先說下這節課講的主要內容,主要有:
David Silver強化學習課程筆記(五)
第五課:模型無關的控制 本文主要介紹模型無關的控制,包括同策略方法(On-Policy,也譯作“在策略”)和異策略(Off-Policy,也譯作“離策略”)方法,由於是模型無關,因此本文聊的是學習(learning),而不是規劃(planning)。
David Silver強化學習課程筆記(一)
大家好,我是微念。 國慶這些天大致學習了一下David Silver的強化學習課程,感覺挺受用的,大家可以去百度雲盤(無字幕版本)下載視訊,或者去B站搜尋觀看(有字幕版本),課程課件下載地址為David Silver課程課件。
David Silver強化學習課程筆記(八)(下)
第八課(下):基於Simulation的搜尋方法 在《第八課(上):學習與規劃的結合》中,我們講到了Model-Based RL方法,在該方法中,我們首先擬合得到一個模型,然後可以利用各種規劃方法進行規劃,或者,可以引申出Sample-Based Plann
David Silver強化學習公開課(一):馬爾科夫決策過程
在強化學習中,馬爾科夫決策過程(Markov decision process, MDP)是對完全可觀測的環境進行描述的,也就是說觀測到的狀態內容完整地決定了決策的需要的特徵。幾乎所有的強化學習問題都可以轉化為MDP。本講是理解強化學習問題的理論基礎。 馬爾科夫過程 M
David Silver強化學習公開課(四):不基於模型的預測
簡介 Introduction 通過先前的講解,我們明白瞭如何從理論上解決一個已知的MDP:通過動態規劃來評估一個給定的策略,並且得到最優價值函式,根據最優價值函式來確定最優策略;也可以直接進行不基於任何策略的狀態價值迭代得到最優價值函式和最優策略。 從本講開始將花連續兩
Andrew Ng機器學習課程筆記(四)之神經網絡
sca 優化 介紹 www 之間 output 現在 利用 href Andrew Ng機器學習課程筆記(四)之神經網絡 版權聲明:本文為博主原創文章,轉載請指明轉載地址 http://www.cnblogs.com/fydeblog/p/7365730.html 前言
機器學習讀書筆記(三)決策樹基礎篇之從相親說起
方法 事務 家裏 分類 筆記 判斷 都是 rom tro 一、決策樹 決策樹是什麽?決策樹(decision tree)是一種基本的分類與回歸方法。舉個通俗易懂的例子,如下圖所示的流程圖就是一個決策樹,長方形代表判斷模塊(decision block),橢圓形成代
Hibernate框架技術視頻課程——筆記(三)
html ble ima 一對一關聯 .html creat 持久 read 抓取 視頻課程鏈接:http://edu.51cto.com/course/10747.html 一、Hibernate關聯關系 1. 實體之間的關系 泛化關系 通過對象之間的繼承來實現
PHP、MySQL和JavaScript學習手冊筆記(三)
php efault ava asc 學習 mys comm 否則 hello 第四章 條件語句 <?php if ($cond<100) { echo "cond <100"; } else { echo "cond >100"; }
Elam的吳恩達深度學習課程筆記(一)
記憶力是真的差,看過的東西要是一直不用的話就會馬上忘記,於是乎有了寫部落格把學過的東西儲存下來,大概就是所謂的集鞏固,分享,後期查閱與一身的思想吧,下面開始正題 深度學習概論 什麼是神經網路 什麼是神經網路呢,我們就以房價預測為例子來描述一個最簡單的神經網路模型。 假設有6間
學習springboot筆記(三)配置springmvc
springboot預設是配置好了SpringMVC的,所以,如果之前有使用SpringMVC的經驗的話,就可以直接在這裡使用了,但是預設的配置往往難以滿足使用的需求,那麼如何來實現springboot中個性化配置的SpringMVC呢? 一、配置檢視解析器
斯坦福深度學習課程筆記(二)
損失函式和優化 官網 ppt 1 損失函式 損失函式是用來定量地分析我們的模型預測效果有多糟糕的函式。損失函式輸出值越大,代表我們的模型效果越糟糕。 損失函式的通用表示: 假設我們的資料集有N個樣本,{(xi,yi)}i=1N\{(x_i,y_i)\}^{N}_
機器學習課程筆記(2)
分類問題(接1) logistic迴歸中的代價函式: 對於原來的迴歸方程, J(θ)=1/m∑1/2(hθ(x)-y)2 與線性迴歸相同,所不同的是線性迴歸中hθ(x)為f(x),logistics中hθ(x)為sigmoid-f(x) 我們先設cost(h
(Stanford CS224d) Deep Learning and NLP課程筆記(三):GloVe與模型的評估
本節課繼續講授word2vec模型的演算法細節,並介紹了一種新的基於共現矩陣的詞向量模型——GloVe模型。最後,本節課重點介紹了word2vec模型評估的兩種方式。 Skip-gram模型 上節課,我們介紹了一個十分簡單的word2vec模型。模型的目標是預測word \(o\)出現在另一個word \(c
學習Mongodb筆記(三)——文件更新中高效的修改器
在MongoDB中,經常會對於文件進行更新,最簡單的更新是用一個新文件完全替換匹配的文件,但是通常我們會對於一小部分更新,所以我們就需要使用原子性的更新修改器,指定對於文件中末些欄位進行更新,更新修改
Andrew Ng機器學習課程筆記(十三)之無監督學習之EM演算法
Preface Jensen’s Inequality(Jensen不等式) Expectation-Maximization Algorithm(EM演算法) Jensen’s Inequality 對於凸函式 令f(x)f(x)為
Andrew NG機器學習課程筆記(十)
特徵選擇嚴格上來說也是模型選擇的一種。這裡不去辨析他們的關係,重點說明問題。假設我們想對維度為n的樣本進行迴歸,然後,n可能大多以至於遠遠大於訓練樣例數。但是我們感覺很多特徵對於結果是無用的,想剔除n中的無用特徵。n個特徵就有2^n種情況。如果我們去列舉這些情況,然後利用交叉驗證去選,太麻煩了。因此需要一些啟
統計學習方法筆記(三)K近鄰演算法
K近鄰法(KNN)是一種基本的分類和迴歸的方法,KNN的基本思想是給出一定數量帶有標籤的訓練樣本,使用這些訓練樣本將特徵空間劃分成許多的子空間,當一個新的測試樣本進來以後,這個測試樣本一定會落在一個超矩形區域內部,然後找到距離這個測試樣本最近的K個訓練樣本,用這些訓練樣本的
tensorflow深度學習實戰筆記(三):使用tensorflow lite把訓練好的模型移植到手機端,編譯成apk檔案
目錄 tensorflow深度學習實戰筆記(二):把訓練好的模型進行固化,講解了如何固化模型以及把pb模型轉換為tflite模型,現在講解如何用官方的demo把生成的ttlite模型移植到手機端。 一、準備工作 1.1模型訓練 1.