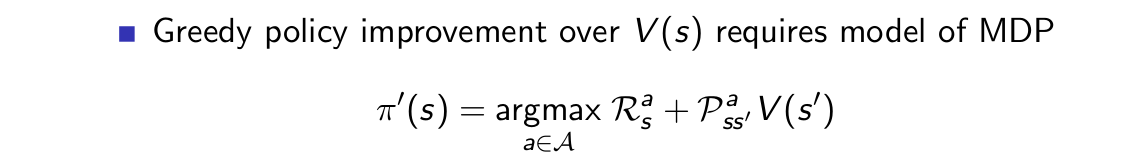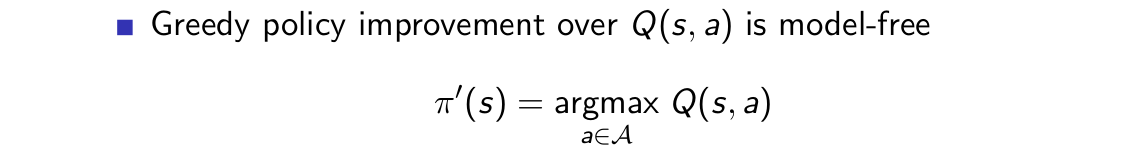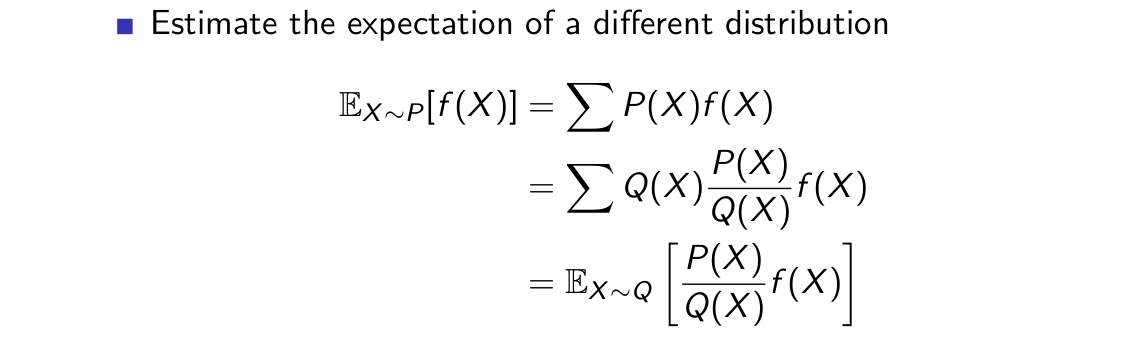第五課：模型無關的控制

        本文主要介紹模型無關的控制，包括同策略方法（On-Policy，也譯作“在策略”）和異策略（Off-Policy，也譯作“離策略”）方法，由於是模型無關，因此本文聊的是學習（learning），而不是規劃（planning）。

       1.簡介

        在第一課中我們說到了預測和控制的區別，這裡就不再贅述，下面我們主要聊一下同策略方法和異策略方法這兩個概念。同策略學習指的是“ Learn on the job ”，確切的說就是用於取樣的策略和我們要學習的策略一致；異策略學習指的是“ Look over someone's shoulder ”，也即我們想要學習的是一個策略，而用於取樣的是另一個策略，舉個簡單的例子，我們想要學習到一個確定性策略，比如利用greedy方法得到的策略，我們直接用該策略進行取樣並不會引入探索，但是我們想要對各個動作和狀態進行探索，那我們就可以使用一個隨機策略進行取樣，比如epsilon-greedy得到的策略。當然，我們的異策略方法不僅僅可以用於引入探索，還可以產生引導樣本，比如我們想要機器人完成抓取任務，可以先讓專家給出示教軌跡樣本，並利用該樣本對抓取策略進行學習，從而有效地減少所需要的樣本數量。

       2.同策略蒙特卡羅控制

        在第三課中我們說到了策略迭代方法，下面我們先來回顧一下：

        我們第三課的主題是利用動態規劃進行"規劃"，也即基於模型的方法，那我們如何將策略迭代方法拓展到"學習"這一問題上呢?

        策略迭代包括兩個部分，策略估計和策略改進，其中策略估計用的是貝爾曼期望方程，策略改進用的是greedy方法。既然我們要將其變為模型無關的方法，那麼首先在策略估計中我們就不能使用貝爾曼期望方程，而是變為sample方法，比如MC方法或TD方法。假如我們選用MC方法對值函式進行估計，得到策略對應的狀態值函式V，然後利用greedy方法得到新策略：

       雖然我們在使用MC方法對策略進行估計的時候沒有使用到模型，但是在上面的策略改進中需要知道模型的知識，即獎勵函式R和轉移概率矩陣P。因此我們並不能使用狀態值函式作為估計的物件。那動作值函式q呢？

        如果我們已經完成了策略估計，那麼我們只需要求一個argmax即可對策略進行改進，所以我們的想法是正確的，可以使用q函式作為估計物件。

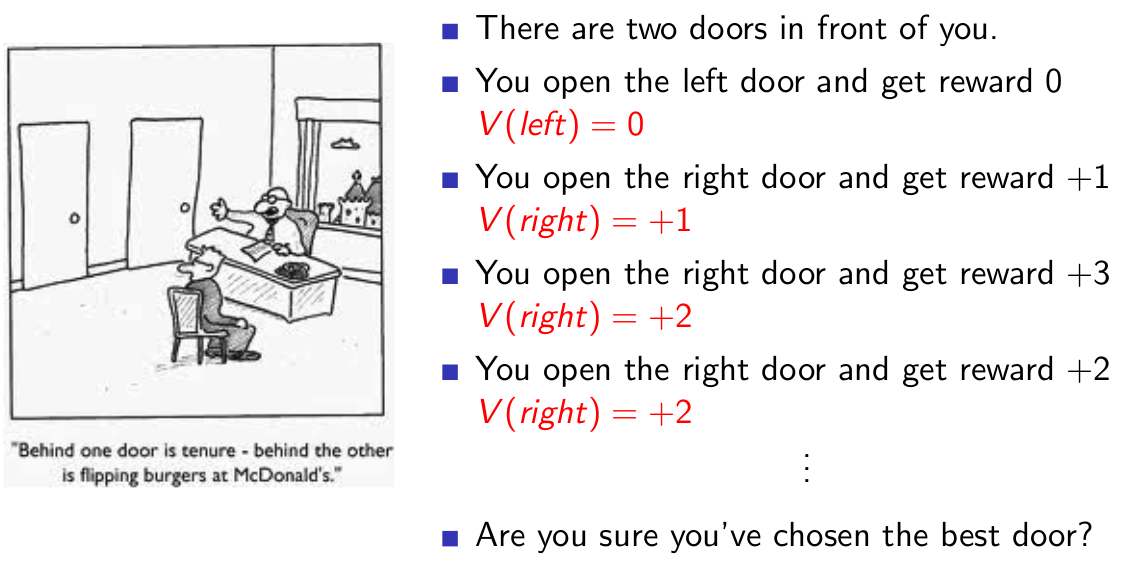
        下面我們考慮策略改進，這裡先直接使用greedy方法，從下面的例子我們會看見，這時我們的策略迭代可能會陷入一個僵局：

        應聘者先打開了左邊的門，得到的獎勵為R=0，所以V(left)=0，然後打開了右邊的門，得到的獎勵為R=1，所以V(right)=+1，因為V(right)>V(left)，所以應聘者會繼續開啟右邊的門，如果右邊的門獲取到的獎勵始終使得V(right)>V(left)成立，則應聘者再也不會開啟左邊的門，哪怕左邊的門中有很大的概率R=100，也即陷入了僵局。

        從這個例子來看，如果我們引入對左邊門的探索，那麼，就可能探索到R=100的獎勵，也就選擇了回報更大的門。所以，學者們提出了epsilon-greedy方法：

        這是一種及其簡單的想法，它保證了在任何一個狀態下，所有動作都有可能被選擇，或者說，它能夠保證足夠的探索。同greedy方法一樣，我們可以很容易地證明epsilon-greedy方法總能對策略進行改進：

        對上面的討論進行總結，我們可以得到蒙特卡羅策略迭代方法：

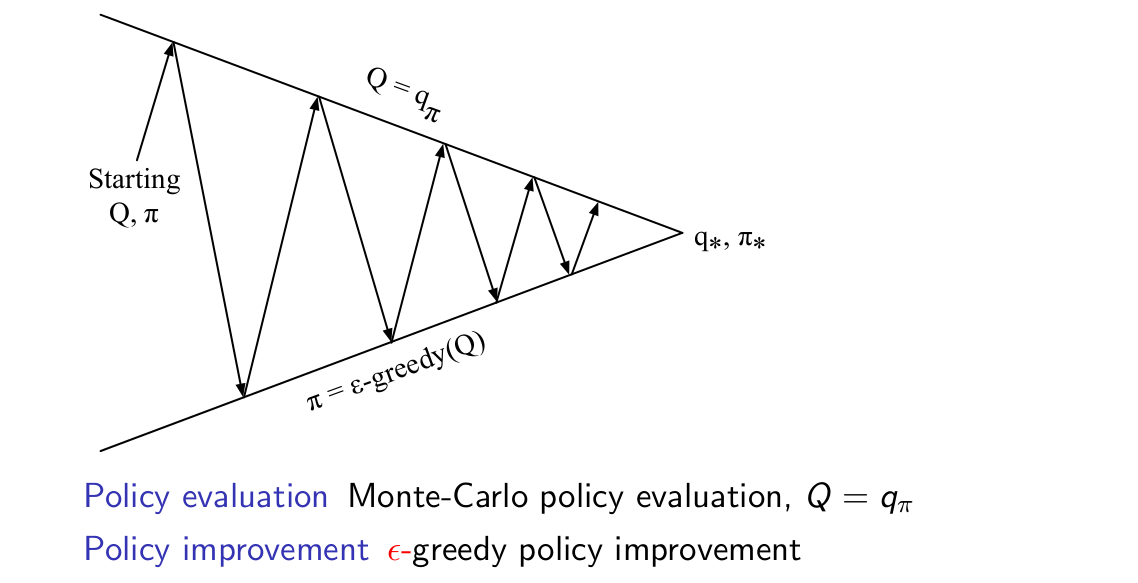
       與我們在第三課中講到的策略迭代方法不一樣，MC策略迭代在估計中用的是q函式，在策略改進中用的是epsilon-greedy方法。在實際應用中，我們稱之為蒙特卡羅控制，且更確切地給出其迭代示意圖：

        我們希望得到一個這樣的學習方法：

        1）在學習開始時有足夠的探索；

        2）最終得到的策略沒有探索，是一個確定性的策略。

        這兩個特點讓我們引出了對於GLIE的定義：

        GLIE滿足兩個條件：

        1）所有的狀態動作對都能夠被探索無數次；

        2）策略最終收斂到一個greedy策略，也即確定性策略。

        比如說，在epsilon-greedy中，如果探索因子epsilon等於1/k，則它是GLIE的。下面我們將GLIE引入到蒙特卡羅控制中：

        無非就是epsilon變為了1/k而已，其他並沒有什麼改變。對於GLIE蒙特卡羅控制的收斂性有如下定理：

       2.同策略時間差分控制

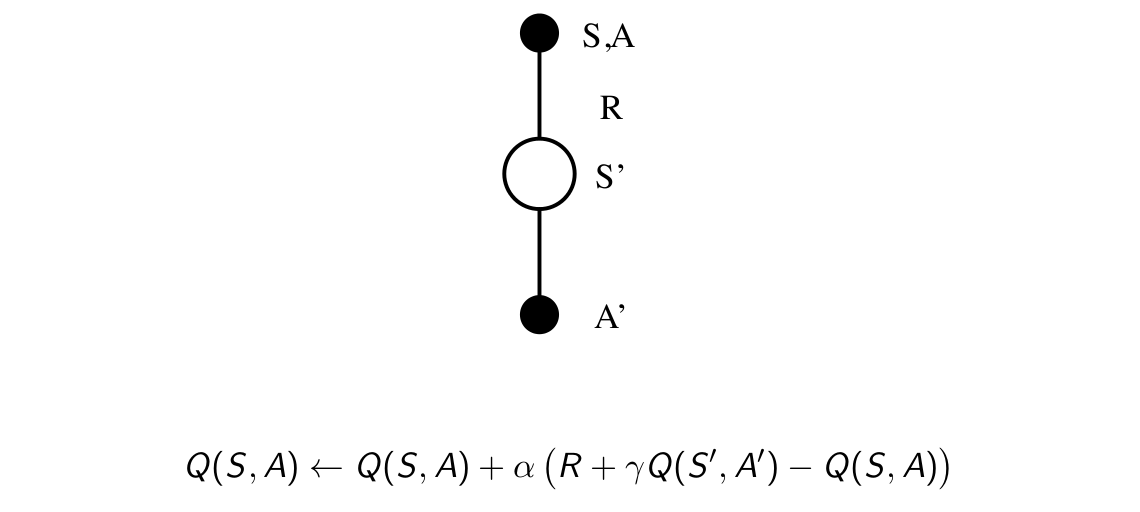
        在第四課中我們提到過，相對於MC方法而言，TD方法有著更低的方差，不需要完成整個episode就能對值函式進行更新，也就是說，可以在episode中的每一個timestep進行線上的值函式估計。說到同策略時間差分控制，一個很自然的想法就是，直接將同策略蒙特卡羅控制中對值函式估計的MC方法換為TD方法，然後將每一個episode對值函式更新一次換為每一個timestep更新一次。我們將這種方法叫做Sarsa，該名字的由來見下圖：

        它的命名就是用影象右邊那一串字母命名的......它的迭代示意圖也很簡單：

        再次強調一下，與同策略蒙特卡羅控制相比，修改了兩個地方，一是策略估計的方法改為了Sarsa，二是每個episode更新一次變為了每個timestep更新一次。下面給出該演算法的具體表述：

        回顧我們前面說的同策略的定義，同策略也即”取樣的策略和我們想要學習的策略一致“，從上面看出，兩者都是對q函式利用epsilon方法匯出來的策略，因而是一致的。設計完演算法之後，總是要考慮一下收斂性的：

        也就是說，如果我們在使用Sarsa方法的過程中，想要保證收斂，就必須要讓上面兩個條件成立，當然，在實際實現中，我們並不會真的去這麼嚴苛地要求其成立。解釋一下Robbins-Monro序列中的兩個條件分別是什麼含義，第一個式子表示從某個初始值開始，我們可以對值函式做出任意多的修正（累積起來很多），第二個式子表示我們對於值函式的修正將變得越來越小（單次修正越來越小）。

        與一般的TD方法一樣，我們可以定義n-step Sarsa：

        然後給出Sarsa(labmda)演算法：

        因為是工程上實現，所以選用的是後向視角方法，在第四章中已經對前後向視角分別給出瞭解釋，不過畢竟是關於狀態值函式V的，所以這裡再給出兩種視角的具體說明，但不再給出解釋：

       3.異策略學習

        如前面所說，在異策略學習中，想要學習的是一個策略，而實際用於取樣的又是另外一個策略，這樣做有什麼好處呢？

        1）可以從人類給出的示教樣本或其他智慧體給出的引導樣本中學習；

        2）可以重用由舊策略生成的經驗；

        3）可以在使用一個探索性策略的同時學習一個確定性策略；

        4）可以用一個策略進行取樣，然後同時學習多個策略。

        其中最為人所知的原因是第三點，也即可以在使用一個探索性策略的同時學習一個確定性策略，Q-learning演算法便是一個很好的例子。在具體介紹異策略學習方法之前，我們先給出重要性取樣的定義：

        可見，重要性取樣實質上是按照兩個概率分佈對函式進行了加權，關於重要性取樣的具體介紹可以參考這篇部落格：取樣方法。

        下面我們將重要性取樣與MC方法和TD方法結合起來：

        從上面兩張ppt可以看出，實質上是利用一個取樣策略得到的target來估計我們想要學習的策略。此外，我們知道，MC方法的方差本來就很大，而重要性取樣將會使得方差急劇增大，因此結合重要性取樣的MC方法就很難用了。對於TD方法來說，其方差本來就比MC要小得多，並且我們僅僅需要行為策略和目標策略在單個時間步上較為相似，因此其加權之後的方差也較小，所以這種方法的實用性較強。

        現在考慮Q-learning演算法，該演算法中的行為策略與目標策略是從同一個值函式q中學習得到，其中目標策略使用greedy方法得到，行為策略使用epsilon-greedy方法得到，因此，重要性取樣的因子pi/mu就有兩種情況了，對於某個狀態s，pi策略選擇動作a的概率要麼是1，要麼是0，當為1時，mu選擇該動作的概率也較大（因為epsilon一般比較小），所以pi/mu約等於1；當為0時，pi/mu=0。因此，雖然Q-learning是一種異策略演算法，它卻不需要重要性取樣因子了，或者說，不需要引入重要性取樣。給出Q-learning演算法的課程ppt供大家參考：

        在Q-learning中，計算TD target使用的是我們期望的策略，也即貪婪策略，而選擇動作使用的策略是e-greedy策略。相當於，我們選擇(狀態，動作)對的時候，是引入探索的，而計算target的時候，是按照期望的貪婪策略進行的。事實上，這裡的Q(S, A')選用e-greedy之後，首先是通過對Q-estimate使用e-greedy來選擇動作A'，然後又用Q-estimate來估計狀態動作對，這樣會使得我們over-estimate Q，所以就有了Double Q-learning演算法，這種演算法首先用Q-estimate來選擇動作A'，接著用Q-target來公平地估計這個狀態動作對，從而減輕了over-estimate問題。關於Double Q-leanring這裡就不詳述了，有興趣的同學可以去看看論文《Deep Reinforcement Learning with Double Q-learning》。

        在Q-learning演算法中，我們只有一個值函式q，行為策略和目標策略均由它產生。如果我們將上面演算法中的target換為R+gamma*Q(S',A')（這裡A'是從行為策略中產生），那麼就是Sarsa演算法了。而這裡使用目標策略對應的值函式構造target，其想法就是朝著目標策略（也即greedy策略）去更新，從而使之收斂到確定性策略對應的值函式。

        值得一提的是，Q-learning也叫做SARSAMAX，記住這一點也就可以很容易地記住Q-learning演算法了。

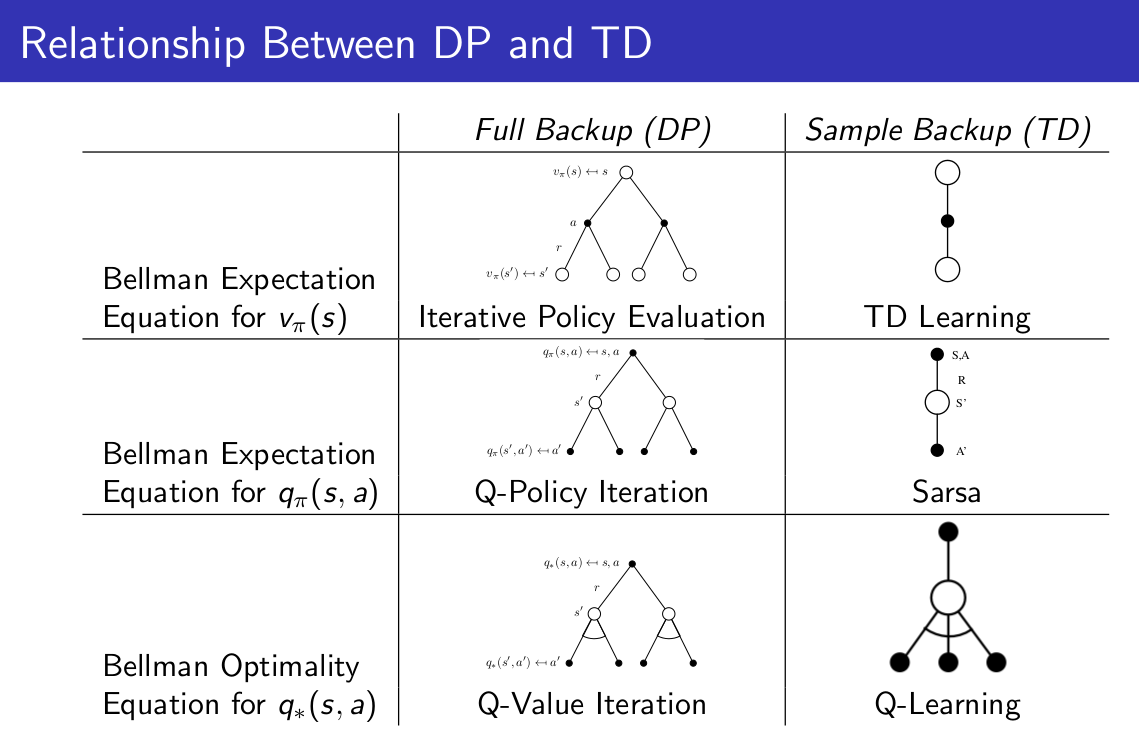
        在本文的最後，給出動態規劃方法與時間差分方法之間的關係表格：

        祝大家工作愉快～