【效能評估】P-R曲線理解
| 負 | 正 | |
| 負 | TN | FP |
| 正 | FN | TP |
把正例正確分類為正例,表示為TP(true positive),把正例錯誤分類為負例,表示為FN(false negative),
把負例正確分類為負例,表示為TN(true negative), 把負例錯誤分類為正例,表示為FP(false positive)
精確率和召回率可以從混淆矩陣中計算而來,precision = TP/(TP + FP), recall = TP/(TP +FN)
那麼P-R曲線是怎麼來的呢?
演算法對樣本進行分類時,都會有置信度,即表示該樣本是正樣本的概率,比如99%的概率認為樣本A是正例,1%的概率認為樣本B是正例。通過選擇合適的閾值,比如50%,對樣本進行劃分,概率大於50%的就認為是正例,小於50%的就是負例。
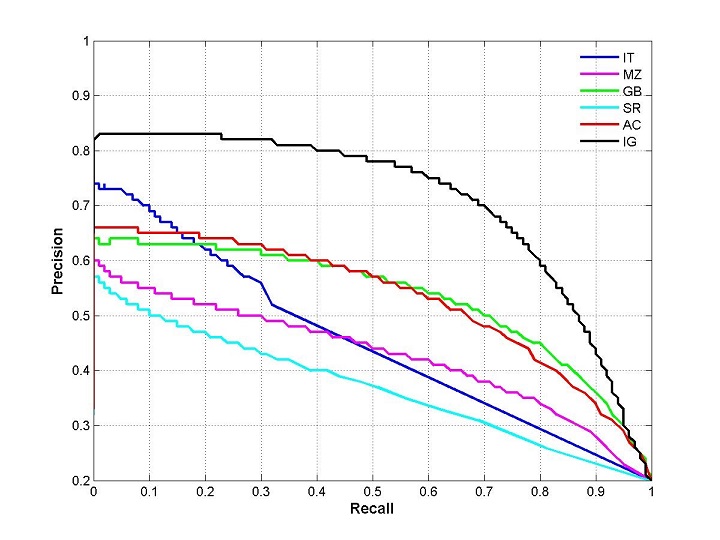
通過置信度就可以對所有樣本進行排序,再逐個樣本的選擇閾值,在該樣本之前的都屬於正例,該樣本之後的都屬於負例。每一個樣本作為劃分閾值時,都可以計算對應的precision和recall,那麼就可以以此繪製曲線。那很多書上、部落格上給出的P-R曲線,都長這樣
當然,這種曲線是有可能的。但是仔細琢磨就會發現一些規律和一些問題。
根據逐個樣本作為閾值劃分點的方法,可以推敲出,recall值是遞增的(但並非嚴格遞增),隨著劃分點左移,正例被判別為正例的越來越多,不會減少。而精確率precision並非遞減,二是有可能振盪的,雖然正例被判為正例的變多,但負例被判為正例的也變多了,因此precision會振盪,但整體趨勢是下降。
另外P-R曲線肯定會經過(0,0)點,比如講所有的樣本全部判為負例,則TP=0,那麼P=R=0,因此會經過(0,0)點,但隨著閾值點左移,precision初始很接近1,recall很接近0,因此有可能從(0,0)上升的線和座標重合,不易區分。如果最前面幾個點都是負例,那麼曲線會從(0,0)點開始逐漸上升。
曲線最終不會到(1,0)點。很多P-R曲線的終點看著都是(1,0)點,這可能是因為負例遠遠多於正例。
最後一個點表示所有的樣本都被判為正例,因此FN=0,所以recall = TP/(TP + FN) = 1, 而FP = 所有的負例樣本數,因此precision = TP/(TP+FP) = 正例的佔所有樣本的比例,故除非負例數很多,否則precision不會為0.
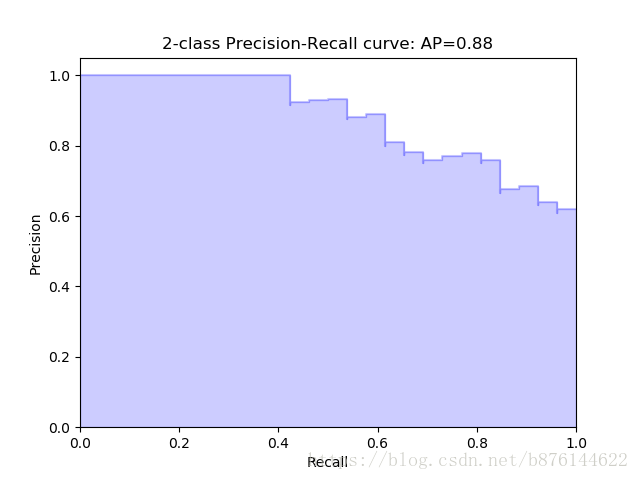
因此,較合理的P-R曲線應該是(曲線一開始被從(0,0)拉昇到(0,1),並且前面的都預測對了,全是正例,因此precision一直是1,)
另外,如果有個劃分點可以把正負樣本完全區分開,那麼P-R曲線就是整個1*1的面積。
總之,P-R曲線應該是從(0,0)開始畫的一條曲線,切割1*1的正方形,得到一塊區域。