樸素貝葉斯法

前言

樸素貝葉斯法是基於貝葉斯定理與特徵條件獨立假設的分類方法，這與我們生活中判斷一件事情的邏輯有點類似，樸素貝葉斯法的核心是引數的估計，在這之前，先來看一下如何用樸素貝葉斯法分類。

程式碼地址https://github.com/bBobxx/statistical-learning,歡迎提問。

基本方法

樸素貝葉斯法必須滿足特徵條件獨立假設，分類時，對給定的輸入\(x\),通過學習到的模型計算後驗概率分佈\(P(Y=c_i|X=x)\),將後驗概率最大的類作為輸出，後驗概率的計算由貝葉斯定理：

\[P(Y=c_k|X=x) = \frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_{k}P(X=x|Y=c_k)P(Y=c_k)}\]

再根據特徵條件獨立假設，

\[P(Y=c_k|X=x) = \frac{P(Y=c_k)\prod_{j}{P(X=x^{(j)}|Y=c_k)}}{\sum_{k}P(Y=c_k)\prod_{j}P(X=x^{(j)}|Y=c_k)}\]

由於分母都一樣，所以我們只比較分子就可以確定類別。

引數估計

對於上面的公式來說，我們需要知道兩個概率，即：

先驗概率：\(P(Y=c_k)=\frac{\sum^{N}_{i=1}I(y_i=c_k)}{N}\)

通俗來說就是數個數然後除以總數。

還有一個條件概率：\(P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum^{N}_{i=1}I(x_{i}^{(j)}=a_{jl},y_i=c_k)}{\sum^{N}_{i=1}I(y_i=c_k)}\)

不要被公式唬住了，看含義就容易懂，其實還是數個數，只不過現在要同時滿足x y的限制，即第i個樣本的第j維特徵\(x_{i}^{(j)}\)取\(a_{jl}\)這個值，並且所屬類別為\(c_k\)的概率。

上面的就是經典的最大似然估計,就是數個數嘛，於此相對的還有貝葉斯學派的引數估計貝葉斯估計，這裡直接給出公式：

先驗概率：\(P(Y=c_k)=\frac{\sum^{N}_{i=1}I(y_i=c_k)+\lambda}{N+K\lambda}\)

條件概率：\(P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum^{N}_{i=1}I(x_{i}^{(j)}=a_{jl},y_i=c_k)+\lambda}{\sum^{N}_{i=1}I(y_i=c_k)+S_j\lambda}\)

通常取\(\lambda=1\),此時叫做拉普拉斯平滑。\(K\)是Y取值的個數，\(S_j\)是某個特徵的可能的取值個數。

程式碼結構

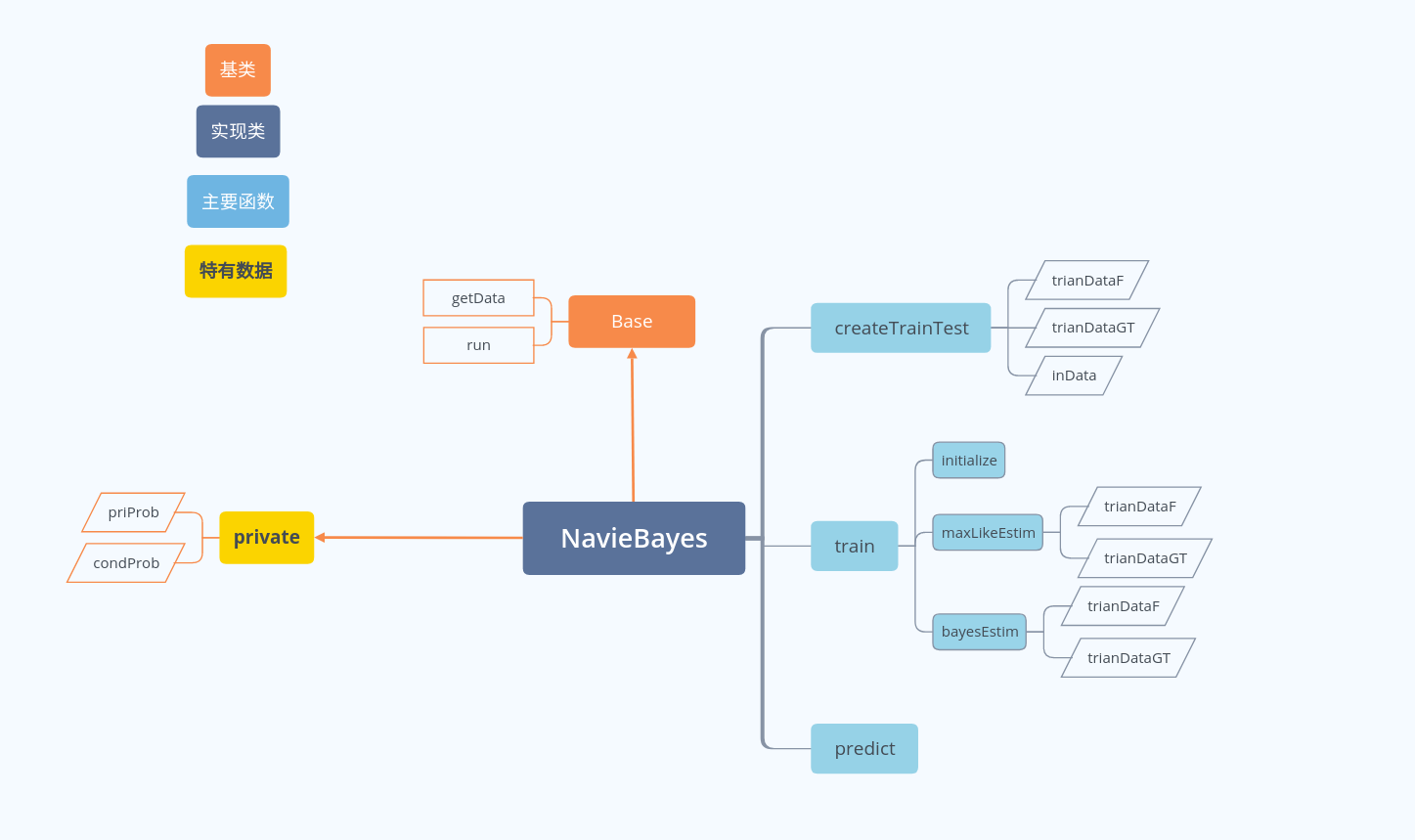
在train裡面分別呼叫了兩種引數估計的方法。

實現細節

對於貝葉斯法，終點在於引數估計，這裡其實就是計數（個人看法，希望得到指導，想破腦袋也沒想起來如何不用遍歷的方法計算概率）。

首先，我選用了map結構來儲存條件概率和先驗概率：

    vector<map<pair<string,string>, double>> condProb;
    map<string, double> priProb;

map是基於紅黑樹的一種資料結構，所以查詢很快，這樣計算後驗概率的時候就能很快查詢到相應的概率。

其他的應該都好理解，無非是迴圈計數，不過在貝葉斯估計這裡我耍了個花招，就是將公式拆成兩部分：\(P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum^{N}_{i=1}I(x_{i}^{(j)}=a_{jl},y_i=c_k)}{\sum^{N}_{i=1}I(y_i=c_k)+S_j\lambda}+\frac{\lambda}{\sum^{N}_{i=1}I(y_i=c_k)+S_j\lambda}\)

void NavieBayes::bayesEstim(const double& lmbda = 1.0){
    for(const auto& gt: trainDataGT){
        priProb[std::to_string(gt)] += 1.0;
    }
    for(unsigned long i=0;i<indim;++i){
        for(unsigned long j=0;j<trainDataF.size();++j)
        {
            auto cond = std::make_pair(std::to_string(trainDataF[j][i]), std::to_string(trainDataGT[j]));

            condProb[i][cond] += 1.0/(priProb[std::to_string(trainDataGT[j])]+lmbda*xVal[i].size());
        }//先跟最大似然估計一樣，由於採用了連加，如果把lambda那部分也包含，需要計算一個每個特徵取某個值時的個數
        //於是將公式拆成兩個分母相同的式子相加的形式，這部分計算分子中除去lambda那部分
    }
    for(unsigned long i=0;i<indim;++i){
        for(auto& d:condProb[i]){
            d.second += lmbda/(priProb[d.first.second]+lmbda*xVal[i].size());
        }
    }//這裡計算另一部分

    for(auto& iter:priProb)
        iter.second = (iter.second+lmbda)/(double(trainDataF.size()+yVal.size()));
}

至於預測就是取\(P(Y=c_k)\prod_{j}{P(X=x^{(j)}|Y=c_k)}\)最大的那一部分

void NavieBayes::predict() {
...
        for(const auto& y: yVal){
            auto pr = priProb[std::to_string(y)];
            for(unsigned long i=0;i<indim;++i)
                pr *= condProb[i][std::make_pair(std::to_string(testDataF[j][i]), std::to_string(y))];
...
    }
}

總結

這部分概念很好懂，但是如何計數確實廢了一番腦筋，以後看看在優化吧，這個時間複雜度實在太高了。