題目：

題目描述

SS城現有兩座監獄，一共關押著NN名罪犯，編號分別為1-N1−N。他們之間的關係自然也極不和諧。很多罪犯之間甚至積怨已久，如果客觀條件具備則隨時可能爆發衝突。我們用“怨氣值”（一個正整數值）來表示某兩名罪犯之間的仇恨程度，怨氣值越大，則這兩名罪犯之間的積怨越多。如果兩名怨氣值為cc 的罪犯被關押在同一監獄，他們倆之間會發生摩擦，並造成影響力為cc的衝突事件。

每年年末，警察局會將本年內監獄中的所有衝突事件按影響力從大到小排成一個列表，然後上報到S 城Z 市長那裡。公務繁忙的Z 市長只會去看列表中的第一個事件的影響力，如果影響很壞，他就會考慮撤換警察局長。

在詳細考察了NN 名罪犯間的矛盾關係後，警察局長覺得壓力巨大。他準備將罪犯們在兩座監獄內重新分配，以求產生的衝突事件影響力都較小，從而保住自己的烏紗帽。假設只要處於同一監獄內的某兩個罪犯間有仇恨，那麼他們一定會在每年的某個時候發生摩擦。

那麼，應如何分配罪犯，才能使Z 市長看到的那個衝突事件的影響力最小？這個最小值是多少？

輸入輸出格式

輸入格式：

每行中兩個數之間用一個空格隔開。第一行為兩個正整數N,MN,M，分別表示罪犯的數目以及存在仇恨的罪犯對數。接下來的MM行每行為三個正整數a_j,b_j,c_jaj​,bj​,cj​，表示a_jaj​ 號和b_jbj​號罪犯之間存在仇恨，其怨氣值為c_jcj​。資料保證1<aj≤bj≤N ,0 < cj≤ 1,000,000,0001<aj≤bj≤N,0<cj≤1,000,000,000，且每對罪犯組合只出現一次。

輸出格式：

共11 行，為ZZ 市長看到的那個衝突事件的影響力。如果本年內監獄中未發生任何衝突事件，請輸出00。

輸入輸出樣例

輸入樣例#1： 複製

4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884

輸出樣例#1： 複製

3512

說明

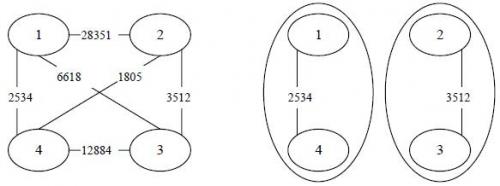
【輸入輸出樣例說明】罪犯之間的怨氣值如下面左圖所示，右圖所示為罪犯的分配方法，市長看到的衝突事件影響力是35123512（由22 號和33 號罪犯引發）。其他任何分法都不會比這個分法更優。

【資料範圍】

對於30\%30%的資料有N≤ 15N≤15。

對於70\%70%的資料有N≤ 2000,M≤ 50000N≤2000,M≤50000。

對於100\%100%的資料有N≤ 20000,M≤ 100000N≤20000,M≤100000。

解題報告：這道題目是在演算法進階上看到的，嘗試著解決了一下用並查集的做法，（主要是想訓練二分染色）但是還是失敗了，第一次見到並查集的這種做法，很奇妙。

題意是什麼不多解釋了，並查集解法：首先咱們應該要明確一個觀點就是優先將大的邊（即仇恨值大的兩個人，放在兩個集合裡）之後如果遇到邊不能放進去了，（放進去之後是矛盾的）就說明沒能放進去的邊是最大的。仇恨值大的已經逐步消失，到最後不能消失的就是剩下的滿足條件的叫警長看到的最大邊。中間涉及了一個敵人陣列，如果他們是可以放到兩個數組裡邊的話，那麼咱們就把二者互設為敵人，敵人的敵人就是朋友。。。

ac程式碼：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long ll;

const int maxn =1e5+100;
int far[maxn],erm[maxn];

struct node{
	int x,y,v;
}num[maxn];
bool cmp(node a,node b)
{
	return a.v>b.v;
}

int find (int x)
{
	if(x==far[x])
		return far[x];
	else
		return far[x]=find(far[x]);
}

void merge(int a,int b)
{
	int pa=find(a);
	int pb=find(b);
	far[pb]=pa;
}
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		far[i]=i;
	for(int i=1;i<=m;i++)
	{
		cin>>num[i].x>>num[i].y>>num[i].v;
	}
	sort(num+1,num+1+m,cmp);
	for(int i=1;i<=m;i++)
	{
		int tmp1=find(num[i].x);
		int tmp2=find(num[i].y);
		if(tmp1==tmp2)
		{
			printf("%d\n",num[i].v);
			return 0;
		}
		if(erm[num[i].x]==0)
			erm[num[i].x]=num[i].y;
		if(erm[num[i].y]==0)
			erm[num[i].y]=num[i].x;
		merge(num[i].x,erm[num[i].y]);
		merge(num[i].y,erm[num[i].x]);	
	}
	printf("0\n");
} 

二分染色解法：咱們一開始就將邊進行排序，利用二分查詢，優先判斷這個中點能不能實現將所有的點都成功染色，如果可以的話，咱們就向左繼續二分，從而找到最小的能夠滿足全部染色的邊，如果不可以的話，就向右繼續二分，至於為啥，我也不知道啊！！，不過這樣是可以保證咱們二分的協調性的，能夠有跳出的條件去實現它，至於是否能夠全部成功染色是寫的遞迴函式，每次都去尋找沒有染色的點去染色，如果可以的話就繼續進行下去，直到成功將所有點都弄好為止（如果中間找不到能夠繼續的點，就結束）（第一次寫，有錯誤請大佬指出）

ac程式碼：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long ll;

const int maxn=2e5+1000;
const int maxnn=1e5+1000;
int n,m,flag;
struct node{
	int v,w,next;
}e[maxn];
bool cmp(int  a,int  b)
{
	return a>b;
}
int cnt=0;
int head[maxn];

void add_edg(int u,int v,int w)
{
	e[++cnt].v=v;
	e[cnt].w=w;
	e[cnt].next=head[u];
	head[u]=cnt;
}
int col[maxn];
int W;
int w[maxn];
int ans;

bool bi(int u)
{
	for(int i=head[u];i;i=e[i].next)
	{
		if(e[i].w<=W) continue;
		int v=e[i].v;
		if(col[u]==col[v]) return false;
		if(!col[v])
		{
			col[v]=3-col[u];//進行染色，成功 
			if(!bi(v)) return false;	//v結點的後續不能夠染色了 
		}
	}
	return true;
}
bool dfs(int u,int fa)
{
	for(int i=head[u];i;i=e[i].next)
	{
		if(e[i].w<=W) continue;
		int v=e[i].v;
		if(v==fa) continue;
		if(col[u]==col[v]) return false;
		if(!col[v])
		{
			col[v]=3-col[u];
			if(!dfs(v,u)) return false;
		}
	}
	return true;
}

bool check()
{
	for(int i=1;i<=n;i++)
	{
		if(!col[i])//如果i點沒有染色 
		{
			col[i]=1;
			if(!bi(i)) return false;//如果i點不能夠繼續向下染色了  結束 
		}
	}
	return true;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		add_edg(a,b,c);
		add_edg(b,a,c);
		w[i]=c;
	}//建圖 
	sort(w+1,w+1+m);//按照邊長進行排序 
	int l=1,r=m;
	while(l<r)//二分尋找最佳 
	{
		int m=(l+r)/2;
		W=w[m];//中值 
		memset(col,0,sizeof(col));
		if(check())//check進行染色 
		{
			ans=w[m];//如果可以的話，存值，然後向左遍歷 ，尋扎是否有更小的值滿足 
			r=m;
		}
		else
		 	l=m+1;//向右跑 ，左邊不能夠實現 
	}
	if(l==1&&r<l) cout<<0;
	else  printf("%d",ans); 
}