Problem

AtCoder-agc005D

題意概要：給出\(n,k\)，求合法的排列個數，其中合法定義為任何數字所在位置與自身值差的絕對值不為\(k\)（即求排列\(\{A_i\}\)，使得\(\forall i\in[1,n],|a_i-i|\not =k\)

Solution

剛看這道題時除了全集取反搞容斥外沒有任何思路啊

\(f_i\)表示排列中至少有\(i\)對衝突的方案數，一對衝突定義為存在一個\(i\)使得\(|a_i-i|=k\)

考慮全集取反，加上一點點容斥思想可得

\[Ans=\sum_{i=0}^n(-1)^i\cdot (n-i)!\cdot f_i\]

至於怎麼得到\(f_i\)

構建一個二分圖：

• 其中\(i\)為數值\(i\)，\(i'\)為\(i\)在排列中的位置編號
• 構建邊為衝突，即所有\(i'\)要和\(i\pm k\)連邊

就像這樣（模擬\(n=4,k=1\)的情況）：

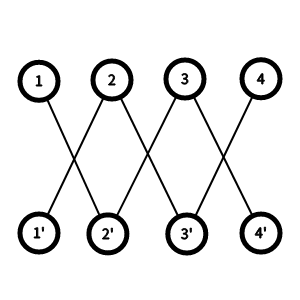
發現這個二分圖中其實只有\(2k\)條鏈，於是可以對這\(2k\)條鏈進行Dp

在某條鏈上：設\(g[i][j][0/1]\)表示考慮前\(i\)個點，且已經有\(j\)對衝突，\(i\)號與\(i+1\)號連與不連的方案數，得出轉移方程：

\[g[i][j][0]=g[i-1][j][0]+g[i-1][j][1]\\g[i][j][1]=g[i-1][j-1][0]\]

對於每條鏈的\(f[i]\)即為\(g[end][i][0]+g[end][i][1]\)（\(end\)為鏈的末尾），最後合併\(2k\)條鏈的時候可以玩揹包

但實際上有個小技巧，就是將\(2k\)條鏈首尾順次相接，在兩條鏈的交界處不轉移第二個方程即可

Code

#include <cstdio>

const int N=2040,p=924844033;
int f[N+N][N][2];
bool end[N+N];
int n,k,Ans,fac[N];

inline int qm(int x){return x<p?x:x-p;}

int main(){
    scanf("%d%d",&n,&k);fac[0]=1;
    for(int i=1;i<=n;++i)fac[i]=1ll*fac[i-1]*i%p;
    for(int i=1,tt=0,d;i<=k;++i){
        d=(n-i)/k+1;
        tt+=d,end[tt]=true;
        tt+=d,end[tt]=true;
    }
    f[1][0][0]=1;
    for(int i=1;i<=n+n;++i)
    for(int j=0;j<=n;++j){
        f[i+1][j][0]=qm(f[i][j][0]+f[i][j][1]);
        if(!end[i])f[i+1][j+1][1]=f[i][j][0];
    }
    for(int i=0,t;i<=n;++i){
        t=1ll*fac[n-i]*qm(f[n+n][i][0]+f[n+n][i][1])%p;
        if(i&1)Ans=qm(Ans-t+p);
        else Ans=qm(Ans+t);
    }
    printf("%d\n",Ans);
    return 0;
}